General framework for online-to-nonconvex conversion: Schedule-free SGD is also effective for nonconvex optimization

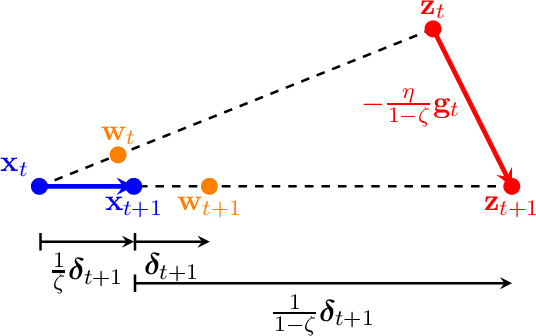
This work investigates the effectiveness of schedule-free methods, developed by A. Defazio et al. (NeurIPS 2024), in nonconvex optimization settings, inspired by their remarkable empirical success in training neural networks. Specifically, we show that schedule-free SGD achieves optimal iteration complexity for nonsmooth, nonconvex optimization problems. Our proof begins with the development of a general framework for online-to-nonconvex conversion, which converts a given online learning algorithm into an optimization algorithm for nonconvex losses. Our general framework not only recovers existing conversions but also leads to two novel conversion schemes. Notably, one of these new conversions corresponds directly to schedule-free SGD, allowing us to establish its optimality. Additionally, our analysis provides valuable insights into the parameter choices for schedule-free SGD, addressing a theoretical gap that the convex theory cannot explain.

Empirical Tests of Optimization Assumptions in Deep Learning

There is a significant gap between our theoretical understanding of optimization algorithms used in deep learning and their practical performance. Theoretical development usually focuses on proving convergence guarantees under a variety of different assumptions, which are themselves often chosen based on a rough combination of intuitive match to practice and analytical convenience. The theory/practice gap may then arise because of the failure to prove a theorem under such assumptions, or because the assumptions do not reflect reality. In this paper, we carefully measure the degree to which these assumptions are capable of explaining modern optimization algorithms by developing new empirical metrics that closely track the key quantities that must be controlled in theoretical analysis. All of our tested assumptions (including typical modern assumptions based on bounds on the Hessian) fail to reliably capture optimization performance. This highlights a need for new empirical verification of analytical assumptions used in theoretical analysis.

Private Zeroth-Order Nonsmooth Nonconvex Optimization

We introduce a new zeroth-order algorithm for private stochastic optimization on nonconvex and nonsmooth objectives. Given a dataset of size $M$, our algorithm ensures $(\alpha,\alpha\rho^2/2)$-R\'enyi differential privacy and finds a $(\delta,\epsilon)$-stationary point so long as $M=\tilde\Omega\left(\frac{d}{\delta\epsilon^3} + \frac{d^{3/2}}{\rho\delta\epsilon^2}\right)$. This matches the optimal complexity of its non-private zeroth-order analog. Notably, although the objective is not smooth, we have privacy ``for free'' whenever $\rho \ge \sqrt{d}\epsilon$.

Fully Unconstrained Online Learning

We provide an online learning algorithm that obtains regret $G\|w_\star\|\sqrt{T\log(\|w_\star\|G\sqrt{T})} + \|w_\star\|^2 + G^2$ on $G$-Lipschitz convex losses for any comparison point $w_\star$ without knowing either $G$ or $\|w_\star\|$. Importantly, this matches the optimal bound $G\|w_\star\|\sqrt{T}$ available with such knowledge (up to logarithmic factors), unless either $\|w_\star\|$ or $G$ is so large that even $G\|w_\star\|\sqrt{T}$ is roughly linear in $T$. Thus, it matches the optimal bound in all cases in which one can achieve sublinear regret, which arguably most "interesting" scenarios.

Online Linear Regression in Dynamic Environments via Discounting

We develop algorithms for online linear regression which achieve optimal static and dynamic regret guarantees \emph{even in the complete absence of prior knowledge}. We present a novel analysis showing that a discounted variant of the Vovk-Azoury-Warmuth forecaster achieves dynamic regret of the form $R_{T}(\vec{u})\le O\left(d\log(T)\vee \sqrt{dP_{T}^{\gamma}(\vec{u})T}\right)$, where $P_{T}^{\gamma}(\vec{u})$ is a measure of variability of the comparator sequence, and show that the discount factor achieving this result can be learned on-the-fly. We show that this result is optimal by providing a matching lower bound. We also extend our results to \emph{strongly-adaptive} guarantees which hold over every sub-interval $[a,b]\subseteq[1,T]$ simultaneously.

Adam with model exponential moving average is effective for nonconvex optimization

In this work, we offer a theoretical analysis of two modern optimization techniques for training large and complex models: (i) adaptive optimization algorithms, such as Adam, and (ii) the model exponential moving average (EMA). Specifically, we demonstrate that a clipped version of Adam with model EMA achieves the optimal convergence rates in various nonconvex optimization settings, both smooth and nonsmooth. Moreover, when the scale varies significantly across different coordinates, we demonstrate that the coordinate-wise adaptivity of Adam is provably advantageous. Notably, unlike previous analyses of Adam, our analysis crucially relies on its core elements -- momentum and discounting factors -- as well as model EMA, motivating their wide applications in practice.

The Road Less Scheduled

Existing learning rate schedules that do not require specification of the optimization stopping step T are greatly out-performed by learning rate schedules that depend on T. We propose an approach that avoids the need for this stopping time by eschewing the use of schedules entirely, while exhibiting state-of-the-art performance compared to schedules across a wide family of problems ranging from convex problems to large-scale deep learning problems. Our Schedule-Free approach introduces no additional hyper-parameters over standard optimizers with momentum. Our method is a direct consequence of a new theory we develop that unifies scheduling and iterate averaging. An open source implementation of our method is available (https://github.com/facebookresearch/schedule_free).

Random Scaling and Momentum for Non-smooth Non-convex Optimization

Training neural networks requires optimizing a loss function that may be highly irregular, and in particular neither convex nor smooth. Popular training algorithms are based on stochastic gradient descent with momentum (SGDM), for which classical analysis applies only if the loss is either convex or smooth. We show that a very small modification to SGDM closes this gap: simply scale the update at each time point by an exponentially distributed random scalar. The resulting algorithm achieves optimal convergence guarantees. Intriguingly, this result is not derived by a specific analysis of SGDM: instead, it falls naturally out of a more general framework for converting online convex optimization algorithms to non-convex optimization algorithms.

When, Why and How Much? Adaptive Learning Rate Scheduling by Refinement

Learning rate schedules used in practice bear little resemblance to those recommended by theory. We close much of this theory/practice gap, and as a consequence are able to derive new problem-adaptive learning rate schedules. Our key technical contribution is a refined analysis of learning rate schedules for a wide class of optimization algorithms (including SGD). In contrast to most prior works that study the convergence of the average iterate, we study the last iterate, which is what most people use in practice. When considering only worst-case analysis, our theory predicts that the best choice is the linear decay schedule: a popular choice in practice that sets the stepsize proportionally to $1 - t/T$, where $t$ is the current iteration and $T$ is the total number of steps. To go beyond this worst-case analysis, we use the observed gradient norms to derive schedules refined for any particular task. These refined schedules exhibit learning rate warm-up and rapid learning rate annealing near the end of training. Ours is the first systematic approach to automatically yield both of these properties. We perform the most comprehensive evaluation of learning rate schedules to date, evaluating across 10 diverse deep learning problems, a series of LLMs, and a suite of logistic regression problems. We validate that overall, the linear-decay schedule matches or outperforms all commonly used default schedules including cosine annealing, and that our schedule refinement method gives further improvements.

Improving Adaptive Online Learning Using Refined Discretization

We study unconstrained Online Linear Optimization with Lipschitz losses. The goal is to simultaneously achieve ($i$) second order gradient adaptivity; and ($ii$) comparator norm adaptivity also known as "parameter freeness" in the literature. Existing regret bounds (Cutkosky and Orabona, 2018; Mhammedi and Koolen, 2020; Jacobsen and Cutkosky, 2022) have the suboptimal $O(\sqrt{V_T\log V_T})$ dependence on the gradient variance $V_T$, while the present work improves it to the optimal rate $O(\sqrt{V_T})$ using a novel continuous-time-inspired algorithm, without any impractical doubling trick. This result can be extended to the setting with unknown Lipschitz constant, eliminating the range ratio problem from prior works (Mhammedi and Koolen, 2020). Concretely, we first show that the aimed simultaneous adaptivity can be achieved fairly easily in a continuous time analogue of the problem, where the environment is modeled by an arbitrary continuous semimartingale. Then, our key innovation is a new discretization argument that preserves such adaptivity in the discrete time adversarial setting. This refines a non-gradient-adaptive discretization argument from (Harvey et al., 2023), both algorithmically and analytically, which could be of independent interest.