The Road Less Scheduled

Existing learning rate schedules that do not require specification of the optimization stopping step T are greatly out-performed by learning rate schedules that depend on T. We propose an approach that avoids the need for this stopping time by eschewing the use of schedules entirely, while exhibiting state-of-the-art performance compared to schedules across a wide family of problems ranging from convex problems to large-scale deep learning problems. Our Schedule-Free approach introduces no additional hyper-parameters over standard optimizers with momentum. Our method is a direct consequence of a new theory we develop that unifies scheduling and iterate averaging. An open source implementation of our method is available (https://github.com/facebookresearch/schedule_free).

Gemini 1.5: Unlocking multimodal understanding across millions of tokens of context

In this report, we present the latest model of the Gemini family, Gemini 1.5 Pro, a highly compute-efficient multimodal mixture-of-experts model capable of recalling and reasoning over fine-grained information from millions of tokens of context, including multiple long documents and hours of video and audio. Gemini 1.5 Pro achieves near-perfect recall on long-context retrieval tasks across modalities, improves the state-of-the-art in long-document QA, long-video QA and long-context ASR, and matches or surpasses Gemini 1.0 Ultra's state-of-the-art performance across a broad set of benchmarks. Studying the limits of Gemini 1.5 Pro's long-context ability, we find continued improvement in next-token prediction and near-perfect retrieval (>99%) up to at least 10M tokens, a generational leap over existing models such as Claude 2.1 (200k) and GPT-4 Turbo (128k). Finally, we highlight surprising new capabilities of large language models at the frontier; when given a grammar manual for Kalamang, a language with fewer than 200 speakers worldwide, the model learns to translate English to Kalamang at a similar level to a person who learned from the same content.

Gemini: A Family of Highly Capable Multimodal Models

This report introduces a new family of multimodal models, Gemini, that exhibit remarkable capabilities across image, audio, video, and text understanding. The Gemini family consists of Ultra, Pro, and Nano sizes, suitable for applications ranging from complex reasoning tasks to on-device memory-constrained use-cases. Evaluation on a broad range of benchmarks shows that our most-capable Gemini Ultra model advances the state of the art in 30 of 32 of these benchmarks - notably being the first model to achieve human-expert performance on the well-studied exam benchmark MMLU, and improving the state of the art in every one of the 20 multimodal benchmarks we examined. We believe that the new capabilities of Gemini models in cross-modal reasoning and language understanding will enable a wide variety of use cases and we discuss our approach toward deploying them responsibly to users.

When, Why and How Much? Adaptive Learning Rate Scheduling by Refinement

Learning rate schedules used in practice bear little resemblance to those recommended by theory. We close much of this theory/practice gap, and as a consequence are able to derive new problem-adaptive learning rate schedules. Our key technical contribution is a refined analysis of learning rate schedules for a wide class of optimization algorithms (including SGD). In contrast to most prior works that study the convergence of the average iterate, we study the last iterate, which is what most people use in practice. When considering only worst-case analysis, our theory predicts that the best choice is the linear decay schedule: a popular choice in practice that sets the stepsize proportionally to $1 - t/T$, where $t$ is the current iteration and $T$ is the total number of steps. To go beyond this worst-case analysis, we use the observed gradient norms to derive schedules refined for any particular task. These refined schedules exhibit learning rate warm-up and rapid learning rate annealing near the end of training. Ours is the first systematic approach to automatically yield both of these properties. We perform the most comprehensive evaluation of learning rate schedules to date, evaluating across 10 diverse deep learning problems, a series of LLMs, and a suite of logistic regression problems. We validate that overall, the linear-decay schedule matches or outperforms all commonly used default schedules including cosine annealing, and that our schedule refinement method gives further improvements.

Mechanic: A Learning Rate Tuner

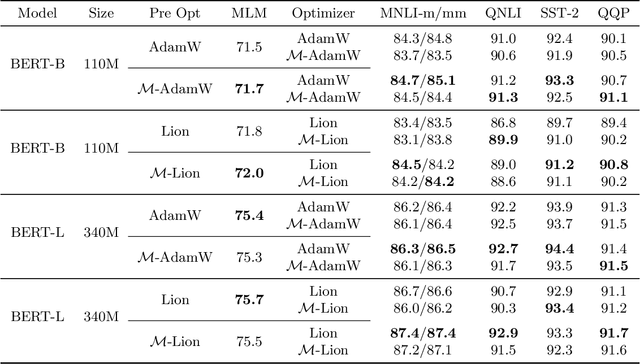
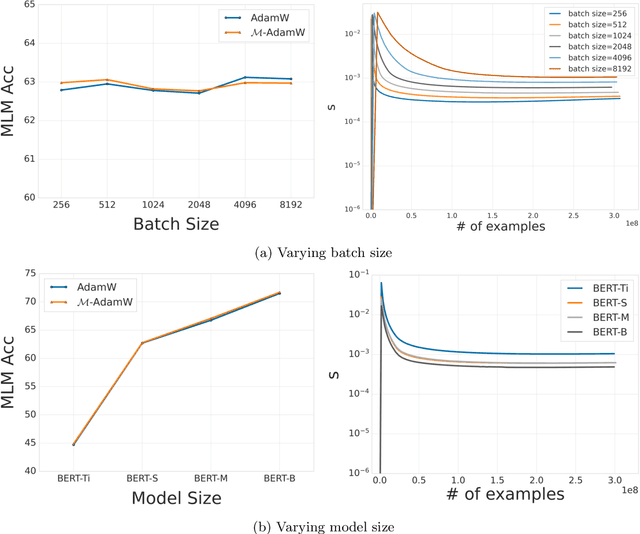
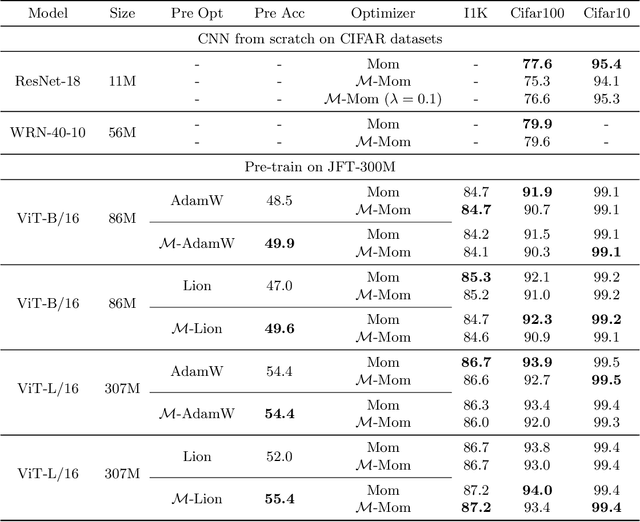
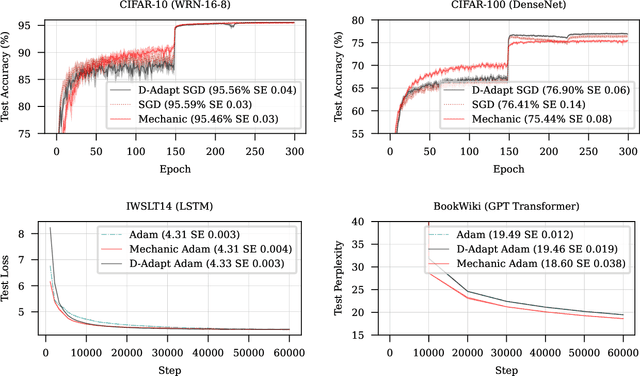
We introduce a technique for tuning the learning rate scale factor of any base optimization algorithm and schedule automatically, which we call \textsc{mechanic}. Our method provides a practical realization of recent theoretical reductions for accomplishing a similar goal in online convex optimization. We rigorously evaluate \textsc{mechanic} on a range of large scale deep learning tasks with varying batch sizes, schedules, and base optimization algorithms. These experiments demonstrate that depending on the problem, \textsc{mechanic} either comes very close to, matches or even improves upon manual tuning of learning rates.

Optimal Stochastic Non-smooth Non-convex Optimization through Online-to-Non-convex Conversion

We present new algorithms for optimizing non-smooth, non-convex stochastic objectives based on a novel analysis technique. This improves the current best-known complexity for finding a $(\delta,\epsilon)$-stationary point from $O(\epsilon^{-4}\delta^{-1})$ stochastic gradient queries to $O(\epsilon^{-3}\delta^{-1})$, which we also show to be optimal. Our primary technique is a reduction from non-smooth non-convex optimization to online learning, after which our results follow from standard regret bounds in online learning. For deterministic and second-order smooth objectives, applying more advanced optimistic online learning techniques enables a new complexity of $O(\epsilon^{-1.5}\delta^{-0.5})$. Our techniques also recover all optimal or best-known results for finding $\epsilon$ stationary points of smooth or second-order smooth objectives in both stochastic and deterministic settings.

Simplifying and Understanding State Space Models with Diagonal Linear RNNs

Sequence models based on linear state spaces (SSMs) have recently emerged as a promising choice of architecture for modeling long range dependencies across various modalities. However, they invariably rely on discretization of a continuous state space, which complicates their presentation and understanding. In this work, we dispose of the discretization step, and propose a model based on vanilla Diagonal Linear RNNs ($\mathrm{DLR}$). We empirically show that $\mathrm{DLR}$ is as performant as previously-proposed SSMs in the presence of strong supervision, despite being conceptually much simpler. Moreover, we characterize the expressivity of SSMs (including $\mathrm{DLR}$) and attention-based models via a suite of $13$ synthetic sequence-to-sequence tasks involving interactions over tens of thousands of tokens, ranging from simple operations, such as shifting an input sequence, to detecting co-dependent visual features over long spatial ranges in flattened images. We find that while SSMs report near-perfect performance on tasks that can be modeled via $\textit{few}$ convolutional kernels, they struggle on tasks requiring $\textit{many}$ such kernels and especially when the desired sequence manipulation is $\textit{context-dependent}$. For example, $\mathrm{DLR}$ learns to perfectly shift a $0.5M$-long input by an arbitrary number of positions but fails when the shift size depends on context. Despite these limitations, $\mathrm{DLR}$ reaches high performance on two higher-order reasoning tasks $\mathrm{ListOpsSubTrees}$ and $\mathrm{PathfinderSegmentation}\text{-}\mathrm{256}$ with input lengths $8K$ and $65K$ respectively, and gives encouraging performance on $\mathrm{PathfinderSegmentation}\text{-}\mathrm{512}$ with input length $262K$ for which attention is not a viable choice.

Differentially Private Image Classification from Features

Leveraging transfer learning has recently been shown to be an effective strategy for training large models with Differential Privacy (DP). Moreover, somewhat surprisingly, recent works have found that privately training just the last layer of a pre-trained model provides the best utility with DP. While past studies largely rely on algorithms like DP-SGD for training large models, in the specific case of privately learning from features, we observe that computational burden is low enough to allow for more sophisticated optimization schemes, including second-order methods. To that end, we systematically explore the effect of design parameters such as loss function and optimization algorithm. We find that, while commonly used logistic regression performs better than linear regression in the non-private setting, the situation is reversed in the private setting. We find that linear regression is much more effective than logistic regression from both privacy and computational aspects, especially at stricter epsilon values ($\epsilon < 1$). On the optimization side, we also explore using Newton's method, and find that second-order information is quite helpful even with privacy, although the benefit significantly diminishes with stricter privacy guarantees. While both methods use second-order information, least squares is effective at lower epsilons while Newton's method is effective at larger epsilon values. To combine the benefits of both, we propose a novel algorithm called DP-FC, which leverages feature covariance instead of the Hessian of the logistic regression loss and performs well across all $\epsilon$ values we tried. With this, we obtain new SOTA results on ImageNet-1k, CIFAR-100 and CIFAR-10 across all values of $\epsilon$ typically considered. Most remarkably, on ImageNet-1K, we obtain top-1 accuracy of 88\% under (8, $8 * 10^{-7}$)-DP and 84.3\% under (0.1, $8 * 10^{-7}$)-DP.

Convexifying Transformers: Improving optimization and understanding of transformer networks

Understanding the fundamental mechanism behind the success of transformer networks is still an open problem in the deep learning literature. Although their remarkable performance has been mostly attributed to the self-attention mechanism, the literature still lacks a solid analysis of these networks and interpretation of the functions learned by them. To this end, we study the training problem of attention/transformer networks and introduce a novel convex analytic approach to improve the understanding and optimization of these networks. Particularly, we first introduce a convex alternative to the self-attention mechanism and reformulate the regularized training problem of transformer networks with our alternative convex attention. Then, we cast the reformulation as a convex optimization problem that is interpretable and easier to optimize. Moreover, as a byproduct of our convex analysis, we reveal an implicit regularization mechanism, which promotes sparsity across tokens. Therefore, we not only improve the optimization of attention/transformer networks but also provide a solid theoretical understanding of the functions learned by them. We also demonstrate the effectiveness of our theory through several numerical experiments.

Long Range Language Modeling via Gated State Spaces

State space models have shown to be effective at modeling long range dependencies, specially on sequence classification tasks. In this work we focus on autoregressive sequence modeling over English books, Github source code and ArXiv mathematics articles. Based on recent developments around the effectiveness of gated activation functions, we propose a new layer named Gated State Space (GSS) and show that it trains significantly faster than the diagonal version of S4 (i.e. DSS) on TPUs, is fairly competitive with several well-tuned Transformer-based baselines and exhibits zero-shot generalization to longer inputs while being straightforward to implement. Finally, we show that leveraging self-attention to model local dependencies improves the performance of GSS even further.