On Design Principles for Private Adaptive Optimizers

The spherical noise added to gradients in differentially private (DP) training undermines the performance of adaptive optimizers like AdaGrad and Adam, and hence many recent works have proposed algorithms to address this challenge. However, the empirical results in these works focus on simple tasks and models and the conclusions may not generalize to model training in practice. In this paper we survey several of these variants, and develop better theoretical intuition for them as well as perform empirical studies comparing them. We find that a common intuition of aiming for unbiased estimates of second moments of gradients in adaptive optimizers is misguided, and instead that a simple technique called scale-then-privatize (which does not achieve unbiased second moments) has more desirable theoretical behaviors and outperforms all other variants we study on a small-scale language model training task. We additionally argue that scale-then-privatize causes the noise addition to better match the application of correlated noise mechanisms which are more desirable to use in practice.

Correlated Noise Mechanisms for Differentially Private Learning

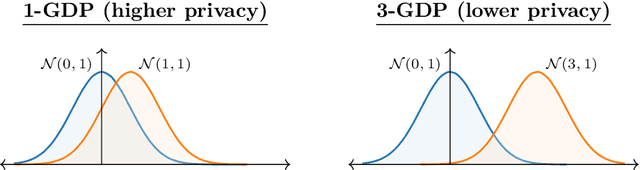
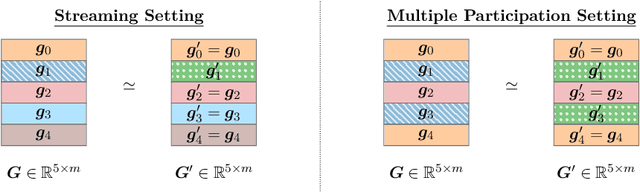
This monograph explores the design and analysis of correlated noise mechanisms for differential privacy (DP), focusing on their application to private training of AI and machine learning models via the core primitive of estimation of weighted prefix sums. While typical DP mechanisms inject independent noise into each step of a stochastic gradient (SGD) learning algorithm in order to protect the privacy of the training data, a growing body of recent research demonstrates that introducing (anti-)correlations in the noise can significantly improve privacy-utility trade-offs by carefully canceling out some of the noise added on earlier steps in subsequent steps. Such correlated noise mechanisms, known variously as matrix mechanisms, factorization mechanisms, and DP-Follow-the-Regularized-Leader (DP-FTRL) when applied to learning algorithms, have also been influential in practice, with industrial deployment at a global scale.

Preserving Expert-Level Privacy in Offline Reinforcement Learning

The offline reinforcement learning (RL) problem aims to learn an optimal policy from historical data collected by one or more behavioural policies (experts) by interacting with an environment. However, the individual experts may be privacy-sensitive in that the learnt policy may retain information about their precise choices. In some domains like personalized retrieval, advertising and healthcare, the expert choices are considered sensitive data. To provably protect the privacy of such experts, we propose a novel consensus-based expert-level differentially private offline RL training approach compatible with any existing offline RL algorithm. We prove rigorous differential privacy guarantees, while maintaining strong empirical performance. Unlike existing work in differentially private RL, we supplement the theory with proof-of-concept experiments on classic RL environments featuring large continuous state spaces, demonstrating substantial improvements over a natural baseline across multiple tasks.

Training Large ASR Encoders with Differential Privacy

Self-supervised learning (SSL) methods for large speech models have proven to be highly effective at ASR. With the interest in public deployment of large pre-trained models, there is a rising concern for unintended memorization and leakage of sensitive data points from the training data. In this paper, we apply differentially private (DP) pre-training to a SOTA Conformer-based encoder, and study its performance on a downstream ASR task assuming the fine-tuning data is public. This paper is the first to apply DP to SSL for ASR, investigating the DP noise tolerance of the BEST-RQ pre-training method. Notably, we introduce a novel variant of model pruning called gradient-based layer freezing that provides strong improvements in privacy-utility-compute trade-offs. Our approach yields a LibriSpeech test-clean/other WER (%) of 3.78/ 8.41 with ($10$, 1e^-9)-DP for extrapolation towards low dataset scales, and 2.81/ 5.89 with (10, 7.9e^-11)-DP for extrapolation towards high scales.

Optimal Rates for DP-SCO with a Single Epoch and Large Batches

The most common algorithms for differentially private (DP) machine learning (ML) are all based on stochastic gradient descent, for example, DP-SGD. These algorithms achieve DP by treating each gradient as an independent private query. However, this independence can cause us to overpay in privacy loss because we don't analyze the entire gradient trajectory. In this work, we propose a new DP algorithm, which we call Accelerated-DP-SRGD (DP stochastic recursive gradient descent), that enables us to break this independence and only pay for privacy in the gradient difference, i.e., in the new information at the current step. Our algorithm achieves the optimal DP-stochastic convex optimization (DP-SCO) error (up to polylog factors) using only a single epoch over the dataset, and converges at the Nesterov's accelerated rate. Our algorithm can be run in at most $\sqrt{n}$ batch gradient steps with batch size at least $\sqrt{n}$, unlike prior work which required $O(n)$ queries with mostly constant batch sizes. To achieve this, our algorithm combines three key ingredients, a variant of stochastic recursive gradients (SRG), accelerated gradient descent, and correlated noise generation from DP continual counting. Finally, we also show that our algorithm improves over existing SoTA on multi-class logistic regression on MNIST and CIFAR-10.

Efficient and Near-Optimal Noise Generation for Streaming Differential Privacy

In the task of differentially private (DP) continual counting, we receive a stream of increments and our goal is to output an approximate running total of these increments, without revealing too much about any specific increment. Despite its simplicity, differentially private continual counting has attracted significant attention both in theory and in practice. Existing algorithms for differentially private continual counting are either inefficient in terms of their space usage or add an excessive amount of noise, inducing suboptimal utility. The most practical DP continual counting algorithms add carefully correlated Gaussian noise to the values. The task of choosing the covariance for this noise can be expressed in terms of factoring the lower-triangular matrix of ones (which computes prefix sums). We present two approaches from this class (for different parameter regimes) that achieve near-optimal utility for DP continual counting and only require logarithmic or polylogarithmic space (and time). Our first approach is based on a space-efficient streaming matrix multiplication algorithm for a class of Toeplitz matrices. We show that to instantiate this algorithm for DP continual counting, it is sufficient to find a low-degree rational function that approximates the square root on a circle in the complex plane. We then apply and extend tools from approximation theory to achieve this. We also derive efficient closed-forms for the objective function for arbitrarily many steps, and show direct numerical optimization yields a highly practical solution to the problem. Our second approach combines our first approach with a recursive construction similar to the binary tree mechanism.

Private Gradient Descent for Linear Regression: Tighter Error Bounds and Instance-Specific Uncertainty Estimation

We provide an improved analysis of standard differentially private gradient descent for linear regression under the squared error loss. Under modest assumptions on the input, we characterize the distribution of the iterate at each time step. Our analysis leads to new results on the algorithm's accuracy: for a proper fixed choice of hyperparameters, the sample complexity depends only linearly on the dimension of the data. This matches the dimension-dependence of the (non-private) ordinary least squares estimator as well as that of recent private algorithms that rely on sophisticated adaptive gradient-clipping schemes (Varshney et al., 2022; Liu et al., 2023). Our analysis of the iterates' distribution also allows us to construct confidence intervals for the empirical optimizer which adapt automatically to the variance of the algorithm on a particular data set. We validate our theorems through experiments on synthetic data.

Private Learning with Public Features

We study a class of private learning problems in which the data is a join of private and public features. This is often the case in private personalization tasks such as recommendation or ad prediction, in which features related to individuals are sensitive, while features related to items (the movies or songs to be recommended, or the ads to be shown to users) are publicly available and do not require protection. A natural question is whether private algorithms can achieve higher utility in the presence of public features. We give a positive answer for multi-encoder models where one of the encoders operates on public features. We develop new algorithms that take advantage of this separation by only protecting certain sufficient statistics (instead of adding noise to the gradient). This method has a guaranteed utility improvement for linear regression, and importantly, achieves the state of the art on two standard private recommendation benchmarks, demonstrating the importance of methods that adapt to the private-public feature separation.

Privacy Amplification for Matrix Mechanisms

Privacy amplification exploits randomness in data selection to provide tighter differential privacy (DP) guarantees. This analysis is key to DP-SGD's success in machine learning, but, is not readily applicable to the newer state-of-the-art algorithms. This is because these algorithms, known as DP-FTRL, use the matrix mechanism to add correlated noise instead of independent noise as in DP-SGD. In this paper, we propose "MMCC", the first algorithm to analyze privacy amplification via sampling for any generic matrix mechanism. MMCC is nearly tight in that it approaches a lower bound as $\epsilon\to0$. To analyze correlated outputs in MMCC, we prove that they can be analyzed as if they were independent, by conditioning them on prior outputs. Our "conditional composition theorem" has broad utility: we use it to show that the noise added to binary-tree-DP-FTRL can asymptotically match the noise added to DP-SGD with amplification. Our amplification algorithm also has practical empirical utility: we show it leads to significant improvement in the privacy-utility trade-offs for DP-FTRL algorithms on standard benchmarks.

Correlated Noise Provably Beats Independent Noise for Differentially Private Learning

Differentially private learning algorithms inject noise into the learning process. While the most common private learning algorithm, DP-SGD, adds independent Gaussian noise in each iteration, recent work on matrix factorization mechanisms has shown empirically that introducing correlations in the noise can greatly improve their utility. We characterize the asymptotic learning utility for any choice of the correlation function, giving precise analytical bounds for linear regression and as the solution to a convex program for general convex functions. We show, using these bounds, how correlated noise provably improves upon vanilla DP-SGD as a function of problem parameters such as the effective dimension and condition number. Moreover, our analytical expression for the near-optimal correlation function circumvents the cubic complexity of the semi-definite program used to optimize the noise correlation matrix in previous work. We validate our theory with experiments on private deep learning. Our work matches or outperforms prior work while being efficient both in terms of compute and memory.