Correlated Noise Mechanisms for Differentially Private Learning

This monograph explores the design and analysis of correlated noise mechanisms for differential privacy (DP), focusing on their application to private training of AI and machine learning models via the core primitive of estimation of weighted prefix sums. While typical DP mechanisms inject independent noise into each step of a stochastic gradient (SGD) learning algorithm in order to protect the privacy of the training data, a growing body of recent research demonstrates that introducing (anti-)correlations in the noise can significantly improve privacy-utility trade-offs by carefully canceling out some of the noise added on earlier steps in subsequent steps. Such correlated noise mechanisms, known variously as matrix mechanisms, factorization mechanisms, and DP-Follow-the-Regularized-Leader (DP-FTRL) when applied to learning algorithms, have also been influential in practice, with industrial deployment at a global scale.

An Inversion Theorem for Buffered Linear Toeplitz (BLT) Matrices and Applications to Streaming Differential Privacy

Buffered Linear Toeplitz (BLT) matrices are a family of parameterized lower-triangular matrices that play an important role in streaming differential privacy with correlated noise. Our main result is a BLT inversion theorem: the inverse of a BLT matrix is itself a BLT matrix with different parameters. We also present an efficient and differentiable $O(d^3)$ algorithm to compute the parameters of the inverse BLT matrix, where $d$ is the degree of the original BLT (typically $d < 10$). Our characterization enables direct optimization of BLT parameters for privacy mechanisms through automatic differentiation.

Fine-Tuning Large Language Models with User-Level Differential Privacy

We investigate practical and scalable algorithms for training large language models (LLMs) with user-level differential privacy (DP) in order to provably safeguard all the examples contributed by each user. We study two variants of DP-SGD with: (1) example-level sampling (ELS) and per-example gradient clipping, and (2) user-level sampling (ULS) and per-user gradient clipping. We derive a novel user-level DP accountant that allows us to compute provably tight privacy guarantees for ELS. Using this, we show that while ELS can outperform ULS in specific settings, ULS generally yields better results when each user has a diverse collection of examples. We validate our findings through experiments in synthetic mean estimation and LLM fine-tuning tasks under fixed compute budgets. We find that ULS is significantly better in settings where either (1) strong privacy guarantees are required, or (2) the compute budget is large. Notably, our focus on LLM-compatible training algorithms allows us to scale to models with hundreds of millions of parameters and datasets with hundreds of thousands of users.

Efficient and Near-Optimal Noise Generation for Streaming Differential Privacy

In the task of differentially private (DP) continual counting, we receive a stream of increments and our goal is to output an approximate running total of these increments, without revealing too much about any specific increment. Despite its simplicity, differentially private continual counting has attracted significant attention both in theory and in practice. Existing algorithms for differentially private continual counting are either inefficient in terms of their space usage or add an excessive amount of noise, inducing suboptimal utility. The most practical DP continual counting algorithms add carefully correlated Gaussian noise to the values. The task of choosing the covariance for this noise can be expressed in terms of factoring the lower-triangular matrix of ones (which computes prefix sums). We present two approaches from this class (for different parameter regimes) that achieve near-optimal utility for DP continual counting and only require logarithmic or polylogarithmic space (and time). Our first approach is based on a space-efficient streaming matrix multiplication algorithm for a class of Toeplitz matrices. We show that to instantiate this algorithm for DP continual counting, it is sufficient to find a low-degree rational function that approximates the square root on a circle in the complex plane. We then apply and extend tools from approximation theory to achieve this. We also derive efficient closed-forms for the objective function for arbitrarily many steps, and show direct numerical optimization yields a highly practical solution to the problem. Our second approach combines our first approach with a recursive construction similar to the binary tree mechanism.

Distributionally Robust Optimization with Bias and Variance Reduction

We consider the distributionally robust optimization (DRO) problem with spectral risk-based uncertainty set and $f$-divergence penalty. This formulation includes common risk-sensitive learning objectives such as regularized condition value-at-risk (CVaR) and average top-$k$ loss. We present Prospect, a stochastic gradient-based algorithm that only requires tuning a single learning rate hyperparameter, and prove that it enjoys linear convergence for smooth regularized losses. This contrasts with previous algorithms that either require tuning multiple hyperparameters or potentially fail to converge due to biased gradient estimates or inadequate regularization. Empirically, we show that Prospect can converge 2-3$\times$ faster than baselines such as stochastic gradient and stochastic saddle-point methods on distribution shift and fairness benchmarks spanning tabular, vision, and language domains.

User Inference Attacks on Large Language Models

Fine-tuning is a common and effective method for tailoring large language models (LLMs) to specialized tasks and applications. In this paper, we study the privacy implications of fine-tuning LLMs on user data. To this end, we define a realistic threat model, called user inference, wherein an attacker infers whether or not a user's data was used for fine-tuning. We implement attacks for this threat model that require only a small set of samples from a user (possibly different from the samples used for training) and black-box access to the fine-tuned LLM. We find that LLMs are susceptible to user inference attacks across a variety of fine-tuning datasets, at times with near perfect attack success rates. Further, we investigate which properties make users vulnerable to user inference, finding that outlier users (i.e. those with data distributions sufficiently different from other users) and users who contribute large quantities of data are most susceptible to attack. Finally, we explore several heuristics for mitigating privacy attacks. We find that interventions in the training algorithm, such as batch or per-example gradient clipping and early stopping fail to prevent user inference. However, limiting the number of fine-tuning samples from a single user can reduce attack effectiveness, albeit at the cost of reducing the total amount of fine-tuning data.

Correlated Noise Provably Beats Independent Noise for Differentially Private Learning

Differentially private learning algorithms inject noise into the learning process. While the most common private learning algorithm, DP-SGD, adds independent Gaussian noise in each iteration, recent work on matrix factorization mechanisms has shown empirically that introducing correlations in the noise can greatly improve their utility. We characterize the asymptotic learning utility for any choice of the correlation function, giving precise analytical bounds for linear regression and as the solution to a convex program for general convex functions. We show, using these bounds, how correlated noise provably improves upon vanilla DP-SGD as a function of problem parameters such as the effective dimension and condition number. Moreover, our analytical expression for the near-optimal correlation function circumvents the cubic complexity of the semi-definite program used to optimize the noise correlation matrix in previous work. We validate our theory with experiments on private deep learning. Our work matches or outperforms prior work while being efficient both in terms of compute and memory.

Towards Federated Foundation Models: Scalable Dataset Pipelines for Group-Structured Learning

We introduce a library, Dataset Grouper, to create large-scale group-structured (e.g., federated) datasets, enabling federated learning simulation at the scale of foundation models. This library allows the creation of group-structured versions of existing datasets based on user-specified partitions, and directly leads to a variety of useful heterogeneous datasets that can be plugged into existing software frameworks. Dataset Grouper offers three key advantages. First, it scales to settings where even a single group's dataset is too large to fit in memory. Second, it provides flexibility, both in choosing the base (non-partitioned) dataset and in defining partitions. Finally, it is framework-agnostic. We empirically demonstrate that Dataset Grouper allows for large-scale federated language modeling simulations on datasets that are orders of magnitude larger than in previous work. Our experimental results show that algorithms like FedAvg operate more as meta-learning methods than as empirical risk minimization methods at this scale, suggesting their utility in downstream personalization and task-specific adaptation.

Unleashing the Power of Randomization in Auditing Differentially Private ML

We present a rigorous methodology for auditing differentially private machine learning algorithms by adding multiple carefully designed examples called canaries. We take a first principles approach based on three key components. First, we introduce Lifted Differential Privacy (LiDP) that expands the definition of differential privacy to handle randomized datasets. This gives us the freedom to design randomized canaries. Second, we audit LiDP by trying to distinguish between the model trained with $K$ canaries versus $K - 1$ canaries in the dataset, leaving one canary out. By drawing the canaries i.i.d., LiDP can leverage the symmetry in the design and reuse each privately trained model to run multiple statistical tests, one for each canary. Third, we introduce novel confidence intervals that take advantage of the multiple test statistics by adapting to the empirical higher-order correlations. Together, this new recipe demonstrates significant improvements in sample complexity, both theoretically and empirically, using synthetic and real data. Further, recent advances in designing stronger canaries can be readily incorporated into the new framework.

Modified Gauss-Newton Algorithms under Noise

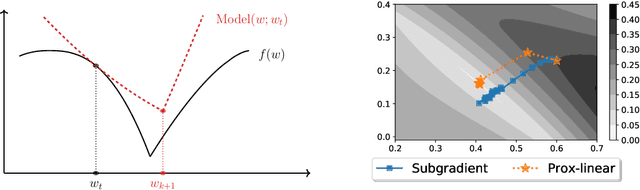
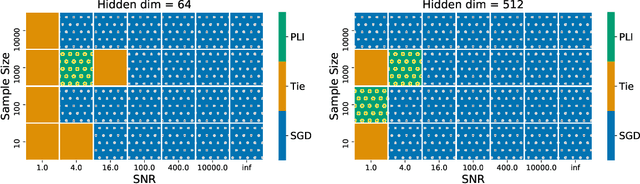
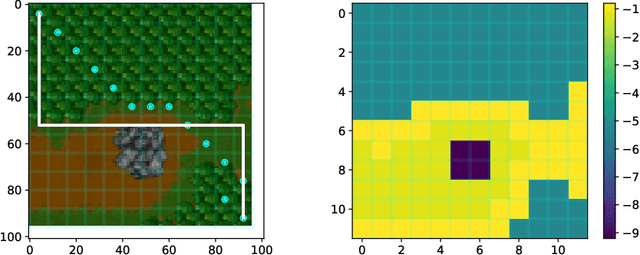
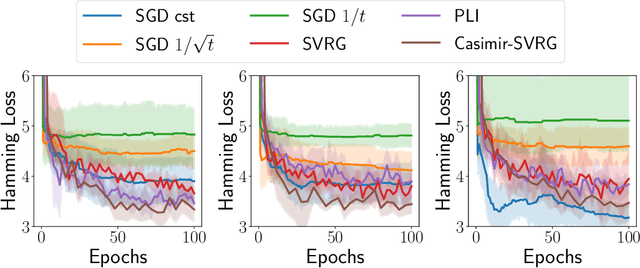
Gauss-Newton methods and their stochastic version have been widely used in machine learning and signal processing. Their nonsmooth counterparts, modified Gauss-Newton or prox-linear algorithms, can lead to contrasting outcomes when compared to gradient descent in large-scale statistical settings. We explore the contrasting performance of these two classes of algorithms in theory on a stylized statistical example, and experimentally on learning problems including structured prediction. In theory, we delineate the regime where the quadratic convergence of the modified Gauss-Newton method is active under statistical noise. In the experiments, we underline the versatility of stochastic (sub)-gradient descent to minimize nonsmooth composite objectives.