Modified Gauss-Newton Algorithms under Noise
Paper and Code
May 18, 2023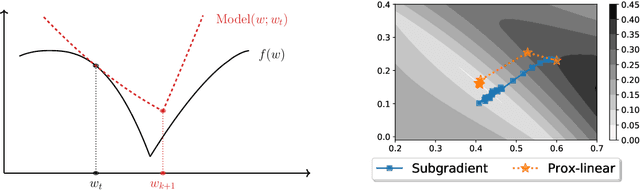
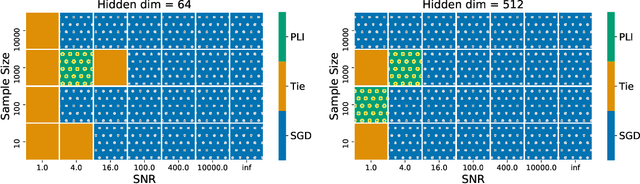
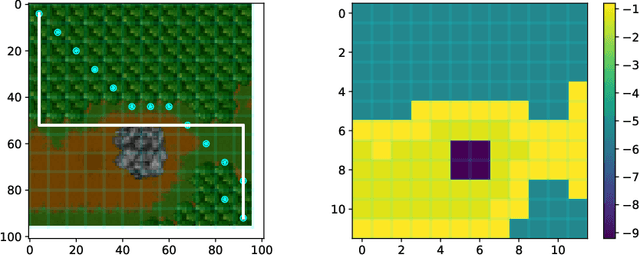
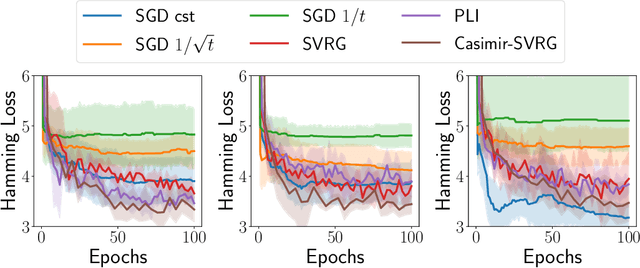
Gauss-Newton methods and their stochastic version have been widely used in machine learning and signal processing. Their nonsmooth counterparts, modified Gauss-Newton or prox-linear algorithms, can lead to contrasting outcomes when compared to gradient descent in large-scale statistical settings. We explore the contrasting performance of these two classes of algorithms in theory on a stylized statistical example, and experimentally on learning problems including structured prediction. In theory, we delineate the regime where the quadratic convergence of the modified Gauss-Newton method is active under statistical noise. In the experiments, we underline the versatility of stochastic (sub)-gradient descent to minimize nonsmooth composite objectives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge