Arun Ganesh
On Design Principles for Private Adaptive Optimizers
Jul 01, 2025Abstract:The spherical noise added to gradients in differentially private (DP) training undermines the performance of adaptive optimizers like AdaGrad and Adam, and hence many recent works have proposed algorithms to address this challenge. However, the empirical results in these works focus on simple tasks and models and the conclusions may not generalize to model training in practice. In this paper we survey several of these variants, and develop better theoretical intuition for them as well as perform empirical studies comparing them. We find that a common intuition of aiming for unbiased estimates of second moments of gradients in adaptive optimizers is misguided, and instead that a simple technique called scale-then-privatize (which does not achieve unbiased second moments) has more desirable theoretical behaviors and outperforms all other variants we study on a small-scale language model training task. We additionally argue that scale-then-privatize causes the noise addition to better match the application of correlated noise mechanisms which are more desirable to use in practice.
Correlated Noise Mechanisms for Differentially Private Learning
Jun 09, 2025
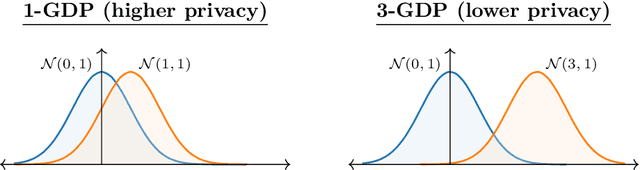

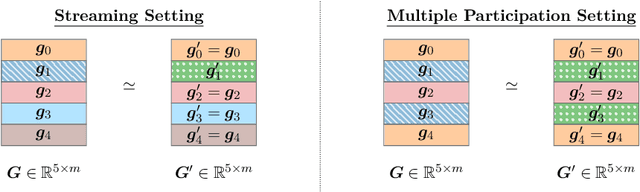
Abstract:This monograph explores the design and analysis of correlated noise mechanisms for differential privacy (DP), focusing on their application to private training of AI and machine learning models via the core primitive of estimation of weighted prefix sums. While typical DP mechanisms inject independent noise into each step of a stochastic gradient (SGD) learning algorithm in order to protect the privacy of the training data, a growing body of recent research demonstrates that introducing (anti-)correlations in the noise can significantly improve privacy-utility trade-offs by carefully canceling out some of the noise added on earlier steps in subsequent steps. Such correlated noise mechanisms, known variously as matrix mechanisms, factorization mechanisms, and DP-Follow-the-Regularized-Leader (DP-FTRL) when applied to learning algorithms, have also been influential in practice, with industrial deployment at a global scale.
It's My Data Too: Private ML for Datasets with Multi-User Training Examples
Mar 05, 2025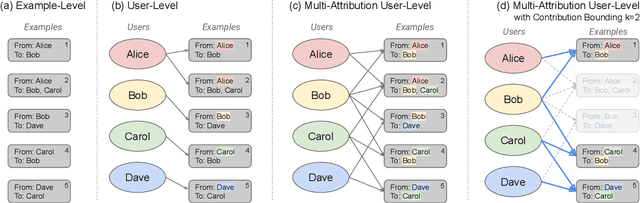
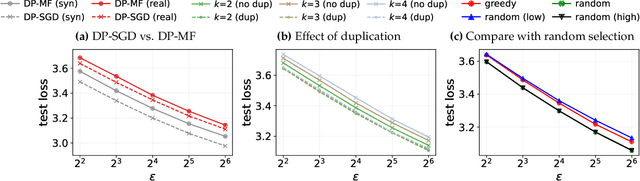
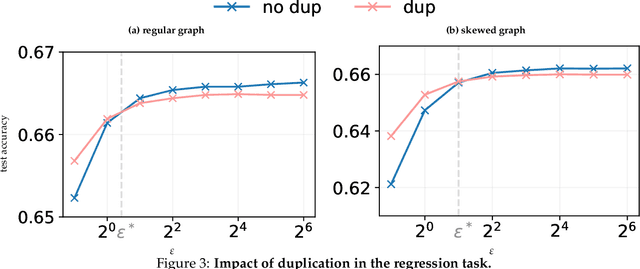
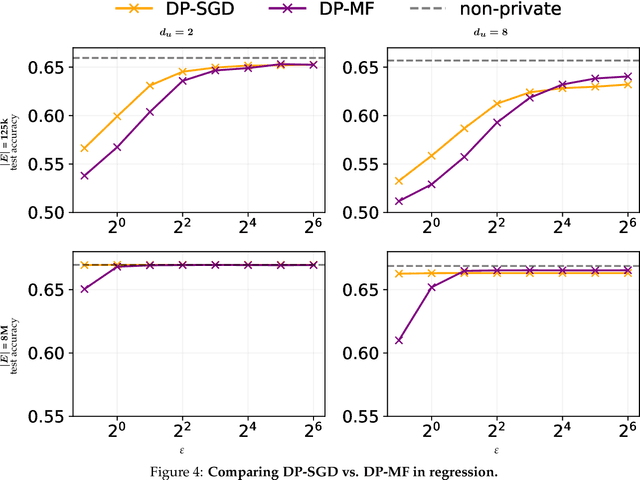
Abstract:We initiate a study of algorithms for model training with user-level differential privacy (DP), where each example may be attributed to multiple users, which we call the multi-attribution model. We first provide a carefully chosen definition of user-level DP under the multi-attribution model. Training in the multi-attribution model is facilitated by solving the contribution bounding problem, i.e. the problem of selecting a subset of the dataset for which each user is associated with a limited number of examples. We propose a greedy baseline algorithm for the contribution bounding problem. We then empirically study this algorithm for a synthetic logistic regression task and a transformer training task, including studying variants of this baseline algorithm that optimize the subset chosen using different techniques and criteria. We find that the baseline algorithm remains competitive with its variants in most settings, and build a better understanding of the practical importance of a bias-variance tradeoff inherent in solutions to the contribution bounding problem.
The Last Iterate Advantage: Empirical Auditing and Principled Heuristic Analysis of Differentially Private SGD
Oct 10, 2024Abstract:We propose a simple heuristic privacy analysis of noisy clipped stochastic gradient descent (DP-SGD) in the setting where only the last iterate is released and the intermediate iterates remain hidden. Namely, our heuristic assumes a linear structure for the model. We show experimentally that our heuristic is predictive of the outcome of privacy auditing applied to various training procedures. Thus it can be used prior to training as a rough estimate of the final privacy leakage. We also probe the limitations of our heuristic by providing some artificial counterexamples where it underestimates the privacy leakage. The standard composition-based privacy analysis of DP-SGD effectively assumes that the adversary has access to all intermediate iterates, which is often unrealistic. However, this analysis remains the state of the art in practice. While our heuristic does not replace a rigorous privacy analysis, it illustrates the large gap between the best theoretical upper bounds and the privacy auditing lower bounds and sets a target for further work to improve the theoretical privacy analyses. We also empirically support our heuristic and show existing privacy auditing attacks are bounded by our heuristic analysis in both vision and language tasks.
Fine-Tuning Large Language Models with User-Level Differential Privacy
Jul 10, 2024Abstract:We investigate practical and scalable algorithms for training large language models (LLMs) with user-level differential privacy (DP) in order to provably safeguard all the examples contributed by each user. We study two variants of DP-SGD with: (1) example-level sampling (ELS) and per-example gradient clipping, and (2) user-level sampling (ULS) and per-user gradient clipping. We derive a novel user-level DP accountant that allows us to compute provably tight privacy guarantees for ELS. Using this, we show that while ELS can outperform ULS in specific settings, ULS generally yields better results when each user has a diverse collection of examples. We validate our findings through experiments in synthetic mean estimation and LLM fine-tuning tasks under fixed compute budgets. We find that ULS is significantly better in settings where either (1) strong privacy guarantees are required, or (2) the compute budget is large. Notably, our focus on LLM-compatible training algorithms allows us to scale to models with hundreds of millions of parameters and datasets with hundreds of thousands of users.
Optimal Rates for DP-SCO with a Single Epoch and Large Batches
Jun 04, 2024Abstract:The most common algorithms for differentially private (DP) machine learning (ML) are all based on stochastic gradient descent, for example, DP-SGD. These algorithms achieve DP by treating each gradient as an independent private query. However, this independence can cause us to overpay in privacy loss because we don't analyze the entire gradient trajectory. In this work, we propose a new DP algorithm, which we call Accelerated-DP-SRGD (DP stochastic recursive gradient descent), that enables us to break this independence and only pay for privacy in the gradient difference, i.e., in the new information at the current step. Our algorithm achieves the optimal DP-stochastic convex optimization (DP-SCO) error (up to polylog factors) using only a single epoch over the dataset, and converges at the Nesterov's accelerated rate. Our algorithm can be run in at most $\sqrt{n}$ batch gradient steps with batch size at least $\sqrt{n}$, unlike prior work which required $O(n)$ queries with mostly constant batch sizes. To achieve this, our algorithm combines three key ingredients, a variant of stochastic recursive gradients (SRG), accelerated gradient descent, and correlated noise generation from DP continual counting. Finally, we also show that our algorithm improves over existing SoTA on multi-class logistic regression on MNIST and CIFAR-10.
Tight Group-Level DP Guarantees for DP-SGD with Sampling via Mixture of Gaussians Mechanisms
Jan 17, 2024

Abstract:We give a procedure for computing group-level $(\epsilon, \delta)$-DP guarantees for DP-SGD, when using Poisson sampling or fixed batch size sampling. Up to discretization errors in the implementation, the DP guarantees computed by this procedure are tight (assuming we release every intermediate iterate).
Privacy Amplification for Matrix Mechanisms
Oct 24, 2023



Abstract:Privacy amplification exploits randomness in data selection to provide tighter differential privacy (DP) guarantees. This analysis is key to DP-SGD's success in machine learning, but, is not readily applicable to the newer state-of-the-art algorithms. This is because these algorithms, known as DP-FTRL, use the matrix mechanism to add correlated noise instead of independent noise as in DP-SGD. In this paper, we propose "MMCC", the first algorithm to analyze privacy amplification via sampling for any generic matrix mechanism. MMCC is nearly tight in that it approaches a lower bound as $\epsilon\to0$. To analyze correlated outputs in MMCC, we prove that they can be analyzed as if they were independent, by conditioning them on prior outputs. Our "conditional composition theorem" has broad utility: we use it to show that the noise added to binary-tree-DP-FTRL can asymptotically match the noise added to DP-SGD with amplification. Our amplification algorithm also has practical empirical utility: we show it leads to significant improvement in the privacy-utility trade-offs for DP-FTRL algorithms on standard benchmarks.
Correlated Noise Provably Beats Independent Noise for Differentially Private Learning
Oct 10, 2023



Abstract:Differentially private learning algorithms inject noise into the learning process. While the most common private learning algorithm, DP-SGD, adds independent Gaussian noise in each iteration, recent work on matrix factorization mechanisms has shown empirically that introducing correlations in the noise can greatly improve their utility. We characterize the asymptotic learning utility for any choice of the correlation function, giving precise analytical bounds for linear regression and as the solution to a convex program for general convex functions. We show, using these bounds, how correlated noise provably improves upon vanilla DP-SGD as a function of problem parameters such as the effective dimension and condition number. Moreover, our analytical expression for the near-optimal correlation function circumvents the cubic complexity of the semi-definite program used to optimize the noise correlation matrix in previous work. We validate our theory with experiments on private deep learning. Our work matches or outperforms prior work while being efficient both in terms of compute and memory.
(Amplified) Banded Matrix Factorization: A unified approach to private training
Jun 13, 2023



Abstract:Matrix factorization (MF) mechanisms for differential privacy (DP) have substantially improved the state-of-the-art in privacy-utility-computation tradeoffs for ML applications in a variety of scenarios, but in both the centralized and federated settings there remain instances where either MF cannot be easily applied, or other algorithms provide better tradeoffs (typically, as $\epsilon$ becomes small). In this work, we show how MF can subsume prior state-of-the-art algorithms in both federated and centralized training settings, across all privacy budgets. The key technique throughout is the construction of MF mechanisms with banded matrices. For cross-device federated learning (FL), this enables multiple-participations with a relaxed device participation schema compatible with practical FL infrastructure (as demonstrated by a production deployment). In the centralized setting, we prove that banded matrices enjoy the same privacy amplification results as for the ubiquitous DP-SGD algorithm, but can provide strictly better performance in most scenarios -- this lets us always at least match DP-SGD, and often outperform it even at $\epsilon\ll2$. Finally, $\hat{b}$-banded matrices substantially reduce the memory and time complexity of per-step noise generation from $\mathcal{O}(n)$, $n$ the total number of iterations, to a constant $\mathcal{O}(\hat{b})$, compared to general MF mechanisms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge