The Last Iterate Advantage: Empirical Auditing and Principled Heuristic Analysis of Differentially Private SGD

We propose a simple heuristic privacy analysis of noisy clipped stochastic gradient descent (DP-SGD) in the setting where only the last iterate is released and the intermediate iterates remain hidden. Namely, our heuristic assumes a linear structure for the model. We show experimentally that our heuristic is predictive of the outcome of privacy auditing applied to various training procedures. Thus it can be used prior to training as a rough estimate of the final privacy leakage. We also probe the limitations of our heuristic by providing some artificial counterexamples where it underestimates the privacy leakage. The standard composition-based privacy analysis of DP-SGD effectively assumes that the adversary has access to all intermediate iterates, which is often unrealistic. However, this analysis remains the state of the art in practice. While our heuristic does not replace a rigorous privacy analysis, it illustrates the large gap between the best theoretical upper bounds and the privacy auditing lower bounds and sets a target for further work to improve the theoretical privacy analyses. We also empirically support our heuristic and show existing privacy auditing attacks are bounded by our heuristic analysis in both vision and language tasks.

Improved Differentially Private and Lazy Online Convex Optimization

We study the task of $(\epsilon, \delta)$-differentially private online convex optimization (OCO). In the online setting, the release of each distinct decision or iterate carries with it the potential for privacy loss. This problem has a long history of research starting with Jain et al. [2012] and the best known results for the regime of {\epsilon} not being very small are presented in Agarwal et al. [2023]. In this paper we improve upon the results of Agarwal et al. [2023] in terms of the dimension factors as well as removing the requirement of smoothness. Our results are now the best known rates for DP-OCO in this regime. Our algorithms builds upon the work of [Asi et al., 2023] which introduced the idea of explicitly limiting the number of switches via rejection sampling. The main innovation in our algorithm is the use of sampling from a strongly log-concave density which allows us to trade-off the dimension factors better leading to improved results.

(Amplified) Banded Matrix Factorization: A unified approach to private training

Matrix factorization (MF) mechanisms for differential privacy (DP) have substantially improved the state-of-the-art in privacy-utility-computation tradeoffs for ML applications in a variety of scenarios, but in both the centralized and federated settings there remain instances where either MF cannot be easily applied, or other algorithms provide better tradeoffs (typically, as $\epsilon$ becomes small). In this work, we show how MF can subsume prior state-of-the-art algorithms in both federated and centralized training settings, across all privacy budgets. The key technique throughout is the construction of MF mechanisms with banded matrices. For cross-device federated learning (FL), this enables multiple-participations with a relaxed device participation schema compatible with practical FL infrastructure (as demonstrated by a production deployment). In the centralized setting, we prove that banded matrices enjoy the same privacy amplification results as for the ubiquitous DP-SGD algorithm, but can provide strictly better performance in most scenarios -- this lets us always at least match DP-SGD, and often outperform it even at $\epsilon\ll2$. Finally, $\hat{b}$-banded matrices substantially reduce the memory and time complexity of per-step noise generation from $\mathcal{O}(n)$, $n$ the total number of iterations, to a constant $\mathcal{O}(\hat{b})$, compared to general MF mechanisms.

Private and Efficient Meta-Learning with Low Rank and Sparse Decomposition

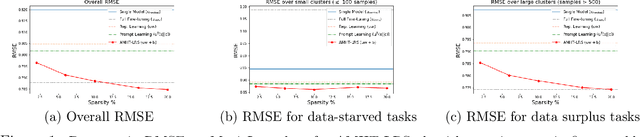
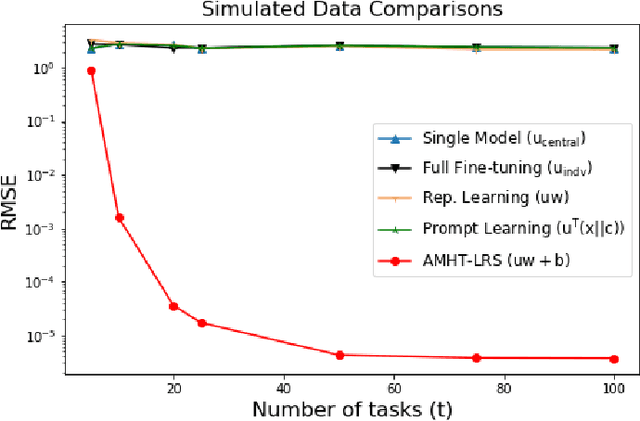
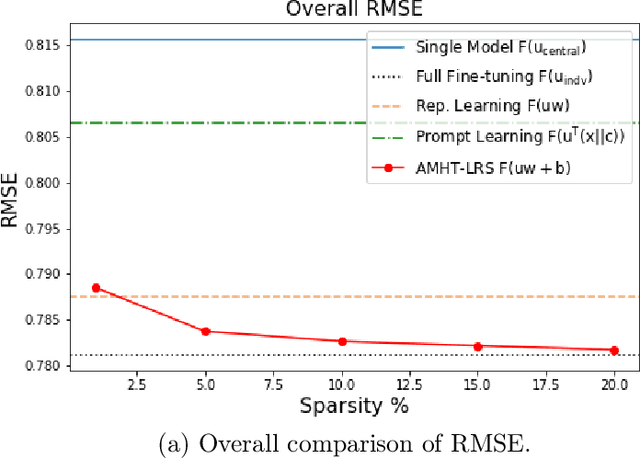
Meta-learning is critical for a variety of practical ML systems -- like personalized recommendations systems -- that are required to generalize to new tasks despite a small number of task-specific training points. Existing meta-learning techniques use two complementary approaches of either learning a low-dimensional representation of points for all tasks, or task-specific fine-tuning of a global model trained using all the tasks. In this work, we propose a novel meta-learning framework that combines both the techniques to enable handling of a large number of data-starved tasks. Our framework models network weights as a sum of low-rank and sparse matrices. This allows us to capture information from multiple domains together in the low-rank part while still allowing task specific personalization using the sparse part. We instantiate and study the framework in the linear setting, where the problem reduces to that of estimating the sum of a rank-$r$ and a $k$-column sparse matrix using a small number of linear measurements. We propose an alternating minimization method with hard thresholding -- AMHT-LRS -- to learn the low-rank and sparse part effectively and efficiently. For the realizable, Gaussian data setting, we show that AMHT-LRS indeed solves the problem efficiently with nearly optimal samples. We extend AMHT-LRS to ensure that it preserves privacy of each individual user in the dataset, while still ensuring strong generalization with nearly optimal number of samples. Finally, on multiple datasets, we demonstrate that the framework allows personalized models to obtain superior performance in the data-scarce regime.

When Does Differentially Private Learning Not Suffer in High Dimensions?

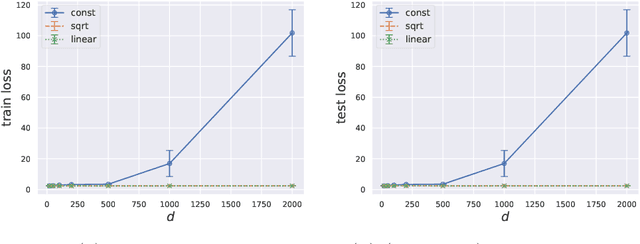
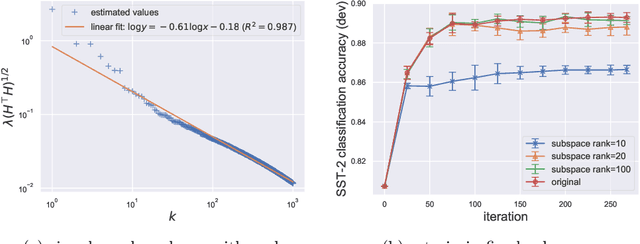
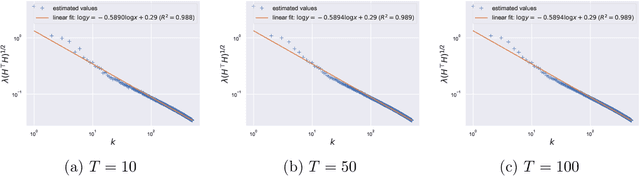
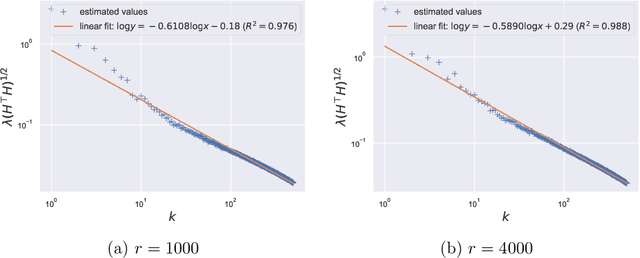
Large pretrained models can be privately fine-tuned to achieve performance approaching that of non-private models. A common theme in these results is the surprising observation that high-dimensional models can achieve favorable privacy-utility trade-offs. This seemingly contradicts known results on the model-size dependence of differentially private convex learning and raises the following research question: When does the performance of differentially private learning not degrade with increasing model size? We identify that the magnitudes of gradients projected onto subspaces is a key factor that determines performance. To precisely characterize this for private convex learning, we introduce a condition on the objective that we term restricted Lipschitz continuity and derive improved bounds for the excess empirical and population risks that are dimension-independent under additional conditions. We empirically show that in private fine-tuning of large language models, gradients evaluated near a local optimum are mostly controlled by a few principal components. This behavior is similar to conditions under which we obtain dimension-independent bounds in convex settings. Our theoretical and empirical results together provide a possible explanation for recent successes in large-scale private fine-tuning.

Private Matrix Approximation and Geometry of Unitary Orbits

Consider the following optimization problem: Given $n \times n$ matrices $A$ and $\Lambda$, maximize $\langle A, U\Lambda U^*\rangle$ where $U$ varies over the unitary group $\mathrm{U}(n)$. This problem seeks to approximate $A$ by a matrix whose spectrum is the same as $\Lambda$ and, by setting $\Lambda$ to be appropriate diagonal matrices, one can recover matrix approximation problems such as PCA and rank-$k$ approximation. We study the problem of designing differentially private algorithms for this optimization problem in settings where the matrix $A$ is constructed using users' private data. We give efficient and private algorithms that come with upper and lower bounds on the approximation error. Our results unify and improve upon several prior works on private matrix approximation problems. They rely on extensions of packing/covering number bounds for Grassmannians to unitary orbits which should be of independent interest.

Private Online Prefix Sums via Optimal Matrix Factorizations

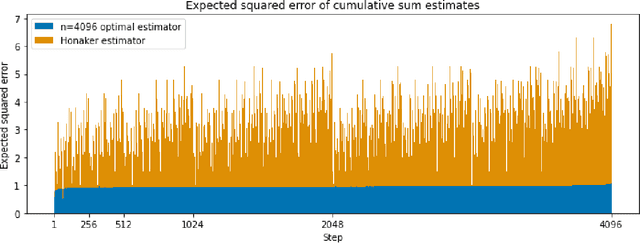
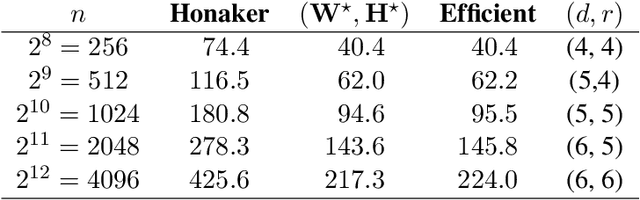
Motivated by differentially-private (DP) training of machine learning models and other applications, we investigate the problem of computing prefix sums in the online (streaming) setting with DP. This problem has previously been addressed by special-purpose tree aggregation schemes with hand-crafted estimators. We show that these previous schemes can all be viewed as specific instances of a broad class of matrix-factorization-based DP mechanisms, and that in fact much better mechanisms exist in this class. In particular, we characterize optimal factorizations of linear queries under online constraints, deriving existence, uniqueness, and explicit expressions that allow us to efficiently compute optimal mechanisms, including for online prefix sums. These solutions improve over the existing state-of-the-art by a significant constant factor, and avoid some of the artifacts introduced by the use of the tree data structure.

Node-Level Differentially Private Graph Neural Networks

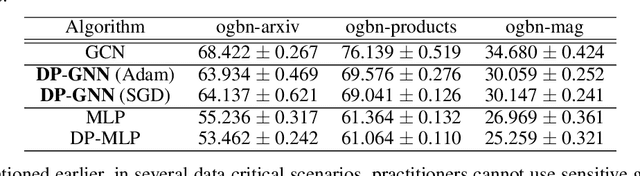
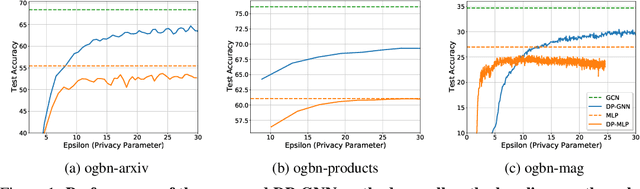
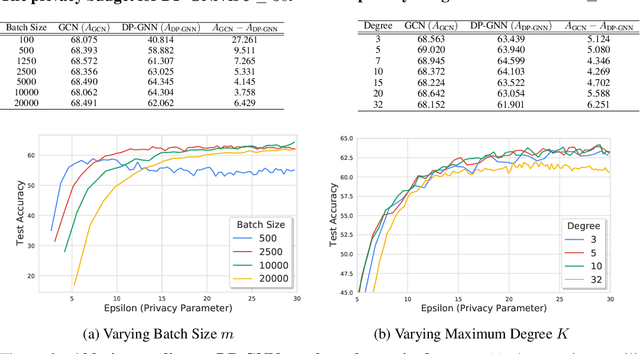
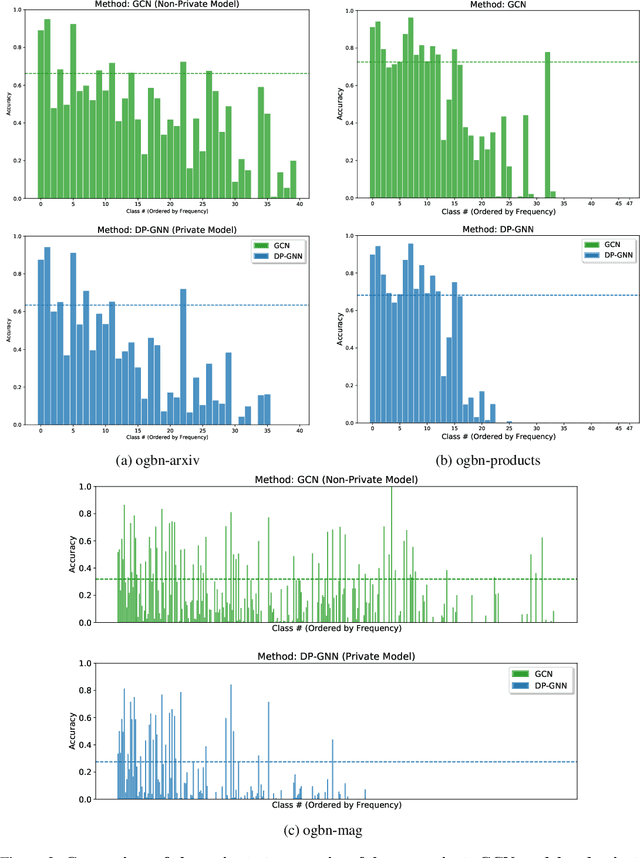
Graph Neural Networks (GNNs) are a popular technique for modelling graph-structured data that compute node-level representations via aggregation of information from the local neighborhood of each node. However, this aggregation implies increased risk of revealing sensitive information, as a node can participate in the inference for multiple nodes. This implies that standard privacy preserving machine learning techniques, such as differentially private stochastic gradient descent (DP-SGD) - which are designed for situations where each data point participates in the inference for one point only - either do not apply, or lead to inaccurate solutions. In this work, we formally define the problem of learning 1-layer GNNs with node-level privacy, and provide an algorithmic solution with a strong differential privacy guarantee. Even though each node can be involved in the inference for multiple nodes, by employing a careful sensitivity analysis anda non-trivial extension of the privacy-by-amplification technique, our method is able to provide accurate solutions with solid privacy parameters. Empirical evaluation on standard benchmarks demonstrates that our method is indeed able to learn accurate privacy preserving GNNs, while still outperforming standard non-private methods that completely ignore graph information.