Unrealized Expectations: Comparing AI Methods vs Classical Algorithms for Maximum Independent Set

AI methods, such as generative models and reinforcement learning, have recently been applied to combinatorial optimization (CO) problems, especially NP-hard ones. This paper compares such GPU-based methods with classical CPU-based methods on Maximum Independent Set (MIS). Experiments on standard graph families show that AI-based algorithms fail to outperform and, in many cases, to match the solution quality of the state-of-art classical solver KaMIS running on a single CPU. Some GPU-based methods even perform similarly to the simplest heuristic, degree-based greedy. Even with post-processing techniques like local search, AI-based methods still perform worse than CPU-based solvers. We develop a new mode of analysis to reveal that non-backtracking AI methods, e.g. LTFT (which is based on GFlowNets), end up reasoning similarly to the simplest degree-based greedy approach, and thus worse than KaMIS. We also find that CPU-based algorithms, notably KaMIS, have strong performance on sparse random graphs, which appears to refute a well-known conjectured upper bound for efficient algorithms from Coja-Oghlan & Efthymiou (2015).

Private Matrix Approximation and Geometry of Unitary Orbits

Consider the following optimization problem: Given $n \times n$ matrices $A$ and $\Lambda$, maximize $\langle A, U\Lambda U^*\rangle$ where $U$ varies over the unitary group $\mathrm{U}(n)$. This problem seeks to approximate $A$ by a matrix whose spectrum is the same as $\Lambda$ and, by setting $\Lambda$ to be appropriate diagonal matrices, one can recover matrix approximation problems such as PCA and rank-$k$ approximation. We study the problem of designing differentially private algorithms for this optimization problem in settings where the matrix $A$ is constructed using users' private data. We give efficient and private algorithms that come with upper and lower bounds on the approximation error. Our results unify and improve upon several prior works on private matrix approximation problems. They rely on extensions of packing/covering number bounds for Grassmannians to unitary orbits which should be of independent interest.

Dissecting Hessian: Understanding Common Structure of Hessian in Neural Networks

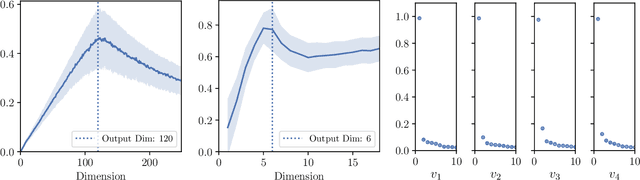
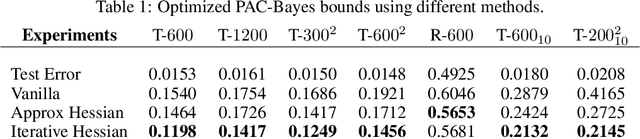
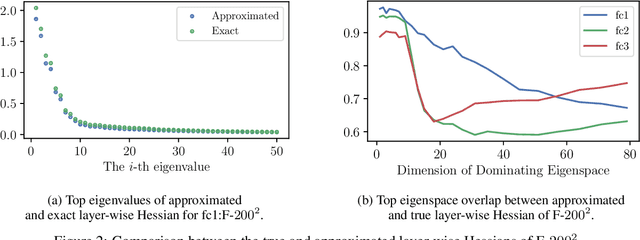
Hessian captures important properties of the deep neural network loss landscape. We observe that eigenvectors and eigenspaces of the layer-wise Hessian for neural network objective have several interesting structures -- top eigenspaces for different models have high overlap, and top eigenvectors form low rank matrices when they are reshaped into the same shape as the corresponding weight matrix. These structures, as well as the low rank structure of the Hessian observed in previous studies, can be explained by approximating the Hessian using Kronecker factorization. Our new understanding can also explain why some of these structures become weaker when the network is trained with batch normalization. Finally, we show that the Kronecker factorization can be combined with PAC-Bayes techniques to get better explicit generalization bounds.