Dissecting Hessian: Understanding Common Structure of Hessian in Neural Networks
Paper and Code
Oct 08, 2020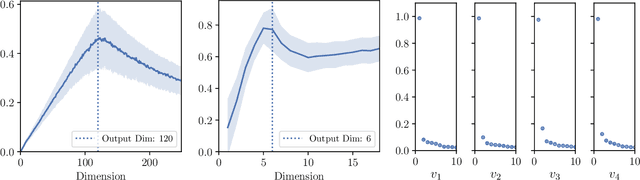
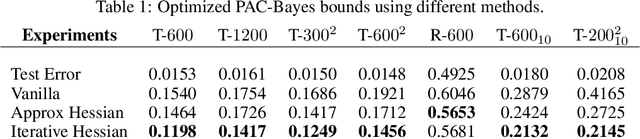
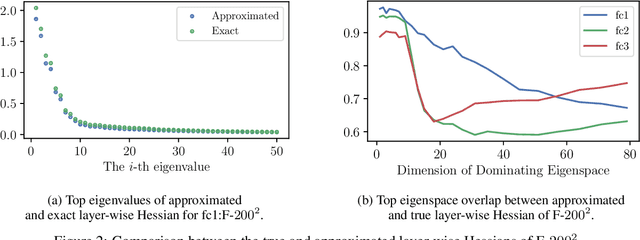
Hessian captures important properties of the deep neural network loss landscape. We observe that eigenvectors and eigenspaces of the layer-wise Hessian for neural network objective have several interesting structures -- top eigenspaces for different models have high overlap, and top eigenvectors form low rank matrices when they are reshaped into the same shape as the corresponding weight matrix. These structures, as well as the low rank structure of the Hessian observed in previous studies, can be explained by approximating the Hessian using Kronecker factorization. Our new understanding can also explain why some of these structures become weaker when the network is trained with batch normalization. Finally, we show that the Kronecker factorization can be combined with PAC-Bayes techniques to get better explicit generalization bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge