Private Online Prefix Sums via Optimal Matrix Factorizations
Paper and Code
Feb 16, 2022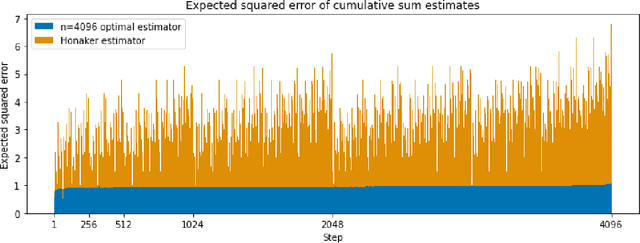
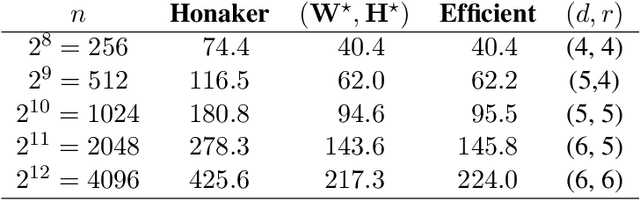
Motivated by differentially-private (DP) training of machine learning models and other applications, we investigate the problem of computing prefix sums in the online (streaming) setting with DP. This problem has previously been addressed by special-purpose tree aggregation schemes with hand-crafted estimators. We show that these previous schemes can all be viewed as specific instances of a broad class of matrix-factorization-based DP mechanisms, and that in fact much better mechanisms exist in this class. In particular, we characterize optimal factorizations of linear queries under online constraints, deriving existence, uniqueness, and explicit expressions that allow us to efficiently compute optimal mechanisms, including for online prefix sums. These solutions improve over the existing state-of-the-art by a significant constant factor, and avoid some of the artifacts introduced by the use of the tree data structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge