Ensemble of Small Classifiers For Imbalanced White Blood Cell Classification

Automating white blood cell classification for diagnosis of leukaemia is a promising alternative to time-consuming and resource-intensive examination of cells by expert pathologists. However, designing robust algorithms for classification of rare cell types remains challenging due to variations in staining, scanning and inter-patient heterogeneity. We propose a lightweight ensemble approach for classification of cells during Haematopoiesis, with a focus on the biology of Granulopoiesis, Monocytopoiesis and Lymphopoiesis. Through dataset expansion to alleviate some class imbalance, we demonstrate that a simple ensemble of lightweight pretrained SwinV2-Tiny, DinoBloom-Small and ConvNeXT-V2-Tiny models achieves excellent performance on this challenging dataset. We train 3 instantiations of each architecture in a stratified 3-fold cross-validation framework; for an input image, we forward-pass through all 9 models and aggregate through logit averaging. We further reason on the weaknesses of our model in confusing similar-looking myelocytes in granulopoiesis and lymphocytes in lymphopoiesis. Code: https://gitlab.com/siddharthsrivastava/wbc-bench-2026.

The Sample Complexity of Membership Inference and Privacy Auditing

A membership-inference attack gets the output of a learning algorithm, and a target individual, and tries to determine whether this individual is a member of the training data or an independent sample from the same distribution. A successful membership-inference attack typically requires the attacker to have some knowledge about the distribution that the training data was sampled from, and this knowledge is often captured through a set of independent reference samples from that distribution. In this work we study how much information the attacker needs for membership inference by investigating the sample complexity-the minimum number of reference samples required-for a successful attack. We study this question in the fundamental setting of Gaussian mean estimation where the learning algorithm is given $n$ samples from a Gaussian distribution $\mathcal{N}(\mu,\Sigma)$ in $d$ dimensions, and tries to estimate $\hat\mu$ up to some error $\mathbb{E}[\|\hat \mu - \mu\|^2_{\Sigma}]\leq \rho^2 d$. Our result shows that for membership inference in this setting, $\Omega(n + n^2 \rho^2)$ samples can be necessary to carry out any attack that competes with a fully informed attacker. Our result is the first to show that the attacker sometimes needs many more samples than the training algorithm uses to train the model. This result has significant implications for practice, as all attacks used in practice have a restricted form that uses $O(n)$ samples and cannot benefit from $\omega(n)$ samples. Thus, these attacks may be underestimating the possibility of membership inference, and better attacks may be possible when information about the distribution is easy to obtain.

Generate-then-Verify: Reconstructing Data from Limited Published Statistics

We study the problem of reconstructing tabular data from aggregate statistics, in which the attacker aims to identify interesting claims about the sensitive data that can be verified with 100% certainty given the aggregates. Successful attempts in prior work have conducted studies in settings where the set of published statistics is rich enough that entire datasets can be reconstructed with certainty. In our work, we instead focus on the regime where many possible datasets match the published statistics, making it impossible to reconstruct the entire private dataset perfectly (i.e., when approaches in prior work fail). We propose the problem of partial data reconstruction, in which the goal of the adversary is to instead output a $\textit{subset}$ of rows and/or columns that are $\textit{guaranteed to be correct}$. We introduce a novel integer programming approach that first $\textbf{generates}$ a set of claims and then $\textbf{verifies}$ whether each claim holds for all possible datasets consistent with the published aggregates. We evaluate our approach on the housing-level microdata from the U.S. Decennial Census release, demonstrating that privacy violations can still persist even when information published about such data is relatively sparse.

It's My Data Too: Private ML for Datasets with Multi-User Training Examples

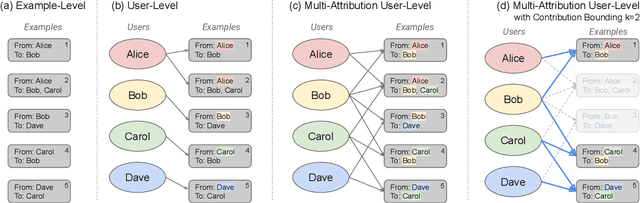
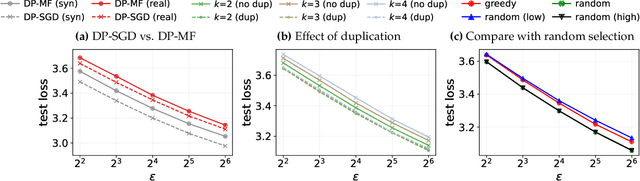
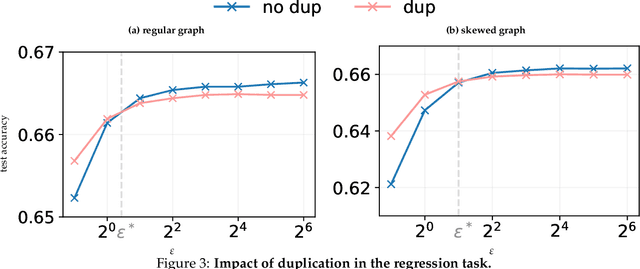
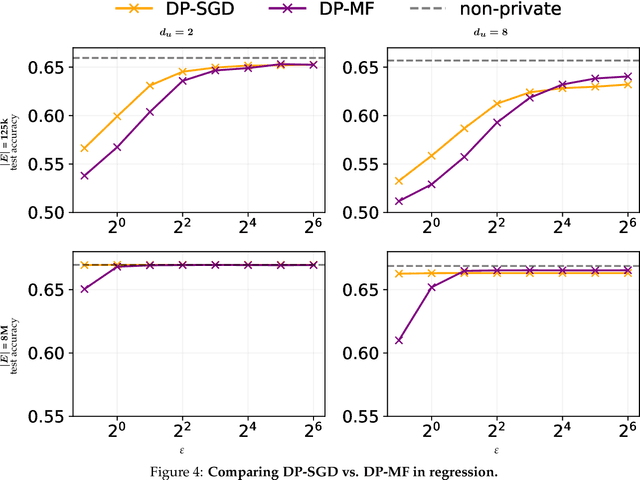
We initiate a study of algorithms for model training with user-level differential privacy (DP), where each example may be attributed to multiple users, which we call the multi-attribution model. We first provide a carefully chosen definition of user-level DP under the multi-attribution model. Training in the multi-attribution model is facilitated by solving the contribution bounding problem, i.e. the problem of selecting a subset of the dataset for which each user is associated with a limited number of examples. We propose a greedy baseline algorithm for the contribution bounding problem. We then empirically study this algorithm for a synthetic logistic regression task and a transformer training task, including studying variants of this baseline algorithm that optimize the subset chosen using different techniques and criteria. We find that the baseline algorithm remains competitive with its variants in most settings, and build a better understanding of the practical importance of a bias-variance tradeoff inherent in solutions to the contribution bounding problem.

Privacy in Metalearning and Multitask Learning: Modeling and Separations

Model personalization allows a set of individuals, each facing a different learning task, to train models that are more accurate for each person than those they could develop individually. The goals of personalization are captured in a variety of formal frameworks, such as multitask learning and metalearning. Combining data for model personalization poses risks for privacy because the output of an individual's model can depend on the data of other individuals. In this work we undertake a systematic study of differentially private personalized learning. Our first main contribution is to construct a taxonomy of formal frameworks for private personalized learning. This taxonomy captures different formal frameworks for learning as well as different threat models for the attacker. Our second main contribution is to prove separations between the personalized learning problems corresponding to different choices. In particular, we prove a novel separation between private multitask learning and private metalearning.

The Last Iterate Advantage: Empirical Auditing and Principled Heuristic Analysis of Differentially Private SGD

We propose a simple heuristic privacy analysis of noisy clipped stochastic gradient descent (DP-SGD) in the setting where only the last iterate is released and the intermediate iterates remain hidden. Namely, our heuristic assumes a linear structure for the model. We show experimentally that our heuristic is predictive of the outcome of privacy auditing applied to various training procedures. Thus it can be used prior to training as a rough estimate of the final privacy leakage. We also probe the limitations of our heuristic by providing some artificial counterexamples where it underestimates the privacy leakage. The standard composition-based privacy analysis of DP-SGD effectively assumes that the adversary has access to all intermediate iterates, which is often unrealistic. However, this analysis remains the state of the art in practice. While our heuristic does not replace a rigorous privacy analysis, it illustrates the large gap between the best theoretical upper bounds and the privacy auditing lower bounds and sets a target for further work to improve the theoretical privacy analyses. We also empirically support our heuristic and show existing privacy auditing attacks are bounded by our heuristic analysis in both vision and language tasks.

Auditing Privacy Mechanisms via Label Inference Attacks

We propose reconstruction advantage measures to audit label privatization mechanisms. A reconstruction advantage measure quantifies the increase in an attacker's ability to infer the true label of an unlabeled example when provided with a private version of the labels in a dataset (e.g., aggregate of labels from different users or noisy labels output by randomized response), compared to an attacker that only observes the feature vectors, but may have prior knowledge of the correlation between features and labels. We consider two such auditing measures: one additive, and one multiplicative. These incorporate previous approaches taken in the literature on empirical auditing and differential privacy. The measures allow us to place a variety of proposed privatization schemes -- some differentially private, some not -- on the same footing. We analyze these measures theoretically under a distributional model which encapsulates reasonable adversarial settings. We also quantify their behavior empirically on real and simulated prediction tasks. Across a range of experimental settings, we find that differentially private schemes dominate or match the privacy-utility tradeoff of more heuristic approaches.

Insufficient Statistics Perturbation: Stable Estimators for Private Least Squares

We present a sample- and time-efficient differentially private algorithm for ordinary least squares, with error that depends linearly on the dimension and is independent of the condition number of $X^\top X$, where $X$ is the design matrix. All prior private algorithms for this task require either $d^{3/2}$ examples, error growing polynomially with the condition number, or exponential time. Our near-optimal accuracy guarantee holds for any dataset with bounded statistical leverage and bounded residuals. Technically, we build on the approach of Brown et al. (2023) for private mean estimation, adding scaled noise to a carefully designed stable nonprivate estimator of the empirical regression vector.

Private Gradient Descent for Linear Regression: Tighter Error Bounds and Instance-Specific Uncertainty Estimation

We provide an improved analysis of standard differentially private gradient descent for linear regression under the squared error loss. Under modest assumptions on the input, we characterize the distribution of the iterate at each time step. Our analysis leads to new results on the algorithm's accuracy: for a proper fixed choice of hyperparameters, the sample complexity depends only linearly on the dimension of the data. This matches the dimension-dependence of the (non-private) ordinary least squares estimator as well as that of recent private algorithms that rely on sophisticated adaptive gradient-clipping schemes (Varshney et al., 2022; Liu et al., 2023). Our analysis of the iterates' distribution also allows us to construct confidence intervals for the empirical optimizer which adapt automatically to the variance of the algorithm on a particular data set. We validate our theorems through experiments on synthetic data.

Metalearning with Very Few Samples Per Task

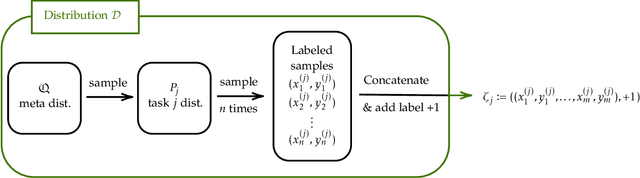
Metalearning and multitask learning are two frameworks for solving a group of related learning tasks more efficiently than we could hope to solve each of the individual tasks on their own. In multitask learning, we are given a fixed set of related learning tasks and need to output one accurate model per task, whereas in metalearning we are given tasks that are drawn i.i.d. from a metadistribution and need to output some common information that can be easily specialized to new, previously unseen tasks from the metadistribution. In this work, we consider a binary classification setting where tasks are related by a shared representation, that is, every task $P$ of interest can be solved by a classifier of the form $f_{P} \circ h$ where $h \in H$ is a map from features to some representation space that is shared across tasks, and $f_{P} \in F$ is a task-specific classifier from the representation space to labels. The main question we ask in this work is how much data do we need to metalearn a good representation? Here, the amount of data is measured in terms of both the number of tasks $t$ that we need to see and the number of samples $n$ per task. We focus on the regime where the number of samples per task is extremely small. Our main result shows that, in a distribution-free setting where the feature vectors are in $\mathbb{R}^d$, the representation is a linear map from $\mathbb{R}^d \to \mathbb{R}^k$, and the task-specific classifiers are halfspaces in $\mathbb{R}^k$, we can metalearn a representation with error $\varepsilon$ using just $n = k+2$ samples per task, and $d \cdot (1/\varepsilon)^{O(k)}$ tasks. Learning with so few samples per task is remarkable because metalearning would be impossible with $k+1$ samples per task, and because we cannot even hope to learn an accurate task-specific classifier with just $k+2$ samples per task.