Privacy in Metalearning and Multitask Learning: Modeling and Separations

Model personalization allows a set of individuals, each facing a different learning task, to train models that are more accurate for each person than those they could develop individually. The goals of personalization are captured in a variety of formal frameworks, such as multitask learning and metalearning. Combining data for model personalization poses risks for privacy because the output of an individual's model can depend on the data of other individuals. In this work we undertake a systematic study of differentially private personalized learning. Our first main contribution is to construct a taxonomy of formal frameworks for private personalized learning. This taxonomy captures different formal frameworks for learning as well as different threat models for the attacker. Our second main contribution is to prove separations between the personalized learning problems corresponding to different choices. In particular, we prove a novel separation between private multitask learning and private metalearning.

Metalearning with Very Few Samples Per Task

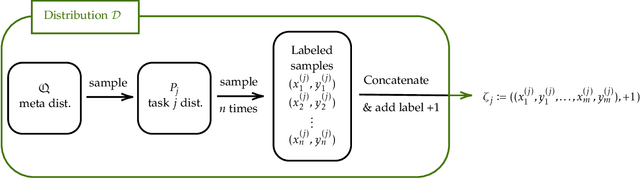
Metalearning and multitask learning are two frameworks for solving a group of related learning tasks more efficiently than we could hope to solve each of the individual tasks on their own. In multitask learning, we are given a fixed set of related learning tasks and need to output one accurate model per task, whereas in metalearning we are given tasks that are drawn i.i.d. from a metadistribution and need to output some common information that can be easily specialized to new, previously unseen tasks from the metadistribution. In this work, we consider a binary classification setting where tasks are related by a shared representation, that is, every task $P$ of interest can be solved by a classifier of the form $f_{P} \circ h$ where $h \in H$ is a map from features to some representation space that is shared across tasks, and $f_{P} \in F$ is a task-specific classifier from the representation space to labels. The main question we ask in this work is how much data do we need to metalearn a good representation? Here, the amount of data is measured in terms of both the number of tasks $t$ that we need to see and the number of samples $n$ per task. We focus on the regime where the number of samples per task is extremely small. Our main result shows that, in a distribution-free setting where the feature vectors are in $\mathbb{R}^d$, the representation is a linear map from $\mathbb{R}^d \to \mathbb{R}^k$, and the task-specific classifiers are halfspaces in $\mathbb{R}^k$, we can metalearn a representation with error $\varepsilon$ using just $n = k+2$ samples per task, and $d \cdot (1/\varepsilon)^{O(k)}$ tasks. Learning with so few samples per task is remarkable because metalearning would be impossible with $k+1$ samples per task, and because we cannot even hope to learn an accurate task-specific classifier with just $k+2$ samples per task.

Multitask Learning via Shared Features: Algorithms and Hardness

We investigate the computational efficiency of multitask learning of Boolean functions over the $d$-dimensional hypercube, that are related by means of a feature representation of size $k \ll d$ shared across all tasks. We present a polynomial time multitask learning algorithm for the concept class of halfspaces with margin $\gamma$, which is based on a simultaneous boosting technique and requires only $\textrm{poly}(k/\gamma)$ samples-per-task and $\textrm{poly}(k\log(d)/\gamma)$ samples in total. In addition, we prove a computational separation, showing that assuming there exists a concept class that cannot be learned in the attribute-efficient model, we can construct another concept class such that can be learned in the attribute-efficient model, but cannot be multitask learned efficiently -- multitask learning this concept class either requires super-polynomial time complexity or a much larger total number of samples.

Fair and Optimal Cohort Selection for Linear Utilities

The rise of algorithmic decision-making has created an explosion of research around the fairness of those algorithms. While there are many compelling notions of individual fairness, beginning with the work of Dwork et al., these notions typically do not satisfy desirable composition properties. To this end, Dwork and Ilvento introduced the fair cohort selection problem, which captures a specific application where a single fair classifier is composed with itself to pick a group of candidates of size exactly $k$. In this work we introduce a specific instance of cohort selection where the goal is to choose a cohort maximizing a linear utility function. We give approximately optimal polynomial-time algorithms for this problem in both an offline setting where the entire fair classifier is given at once, or an online setting where candidates arrive one at a time and are classified as they arrive.