Is API Access to LLMs Useful for Generating Private Synthetic Tabular Data?

Differentially private (DP) synthetic data is a versatile tool for enabling the analysis of private data. Recent advancements in large language models (LLMs) have inspired a number of algorithm techniques for improving DP synthetic data generation. One family of approaches uses DP finetuning on the foundation model weights; however, the model weights for state-of-the-art models may not be public. In this work we propose two DP synthetic tabular data algorithms that only require API access to the foundation model. We adapt the Private Evolution algorithm (Lin et al., 2023; Xie et al., 2024) -- which was designed for image and text data -- to the tabular data domain. In our extension of Private Evolution, we define a query workload-based distance measure, which may be of independent interest. We propose a family of algorithms that use one-shot API access to LLMs, rather than adaptive queries to the LLM. Our findings reveal that API-access to powerful LLMs does not always improve the quality of DP synthetic data compared to established baselines that operate without such access. We provide insights into the underlying reasons and propose improvements to LLMs that could make them more effective for this application.

Privacy in Metalearning and Multitask Learning: Modeling and Separations

Model personalization allows a set of individuals, each facing a different learning task, to train models that are more accurate for each person than those they could develop individually. The goals of personalization are captured in a variety of formal frameworks, such as multitask learning and metalearning. Combining data for model personalization poses risks for privacy because the output of an individual's model can depend on the data of other individuals. In this work we undertake a systematic study of differentially private personalized learning. Our first main contribution is to construct a taxonomy of formal frameworks for private personalized learning. This taxonomy captures different formal frameworks for learning as well as different threat models for the attacker. Our second main contribution is to prove separations between the personalized learning problems corresponding to different choices. In particular, we prove a novel separation between private multitask learning and private metalearning.

Measuring memorization through probabilistic discoverable extraction

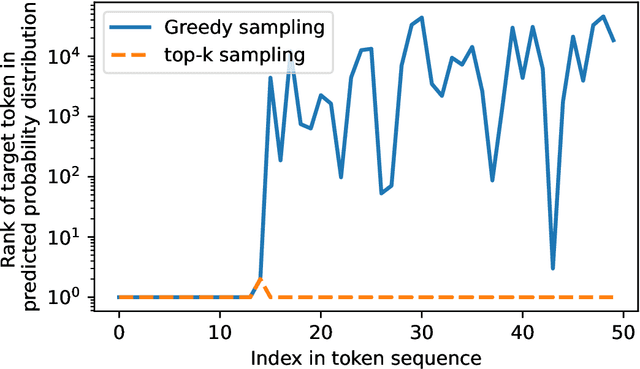
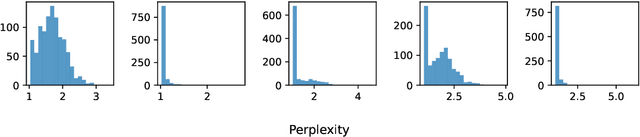
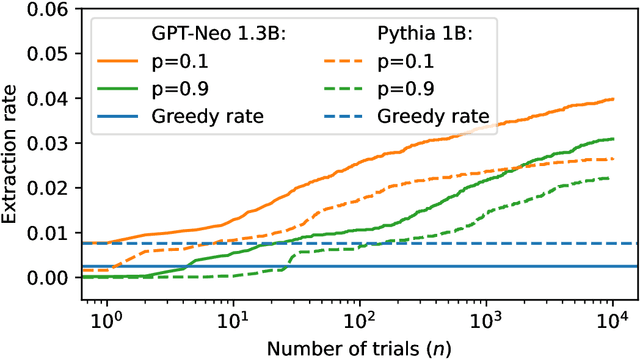
Large language models (LLMs) are susceptible to memorizing training data, raising concerns due to the potential extraction of sensitive information. Current methods to measure memorization rates of LLMs, primarily discoverable extraction (Carlini et al., 2022), rely on single-sequence greedy sampling, potentially underestimating the true extent of memorization. This paper introduces a probabilistic relaxation of discoverable extraction that quantifies the probability of extracting a target sequence within a set of generated samples, considering various sampling schemes and multiple attempts. This approach addresses the limitations of reporting memorization rates through discoverable extraction by accounting for the probabilistic nature of LLMs and user interaction patterns. Our experiments demonstrate that this probabilistic measure can reveal cases of higher memorization rates compared to rates found through discoverable extraction. We further investigate the impact of different sampling schemes on extractability, providing a more comprehensive and realistic assessment of LLM memorization and its associated risks. Our contributions include a new probabilistic memorization definition, empirical evidence of its effectiveness, and a thorough evaluation across different models, sizes, sampling schemes, and training data repetitions.

Auditing Privacy Mechanisms via Label Inference Attacks

We propose reconstruction advantage measures to audit label privatization mechanisms. A reconstruction advantage measure quantifies the increase in an attacker's ability to infer the true label of an unlabeled example when provided with a private version of the labels in a dataset (e.g., aggregate of labels from different users or noisy labels output by randomized response), compared to an attacker that only observes the feature vectors, but may have prior knowledge of the correlation between features and labels. We consider two such auditing measures: one additive, and one multiplicative. These incorporate previous approaches taken in the literature on empirical auditing and differential privacy. The measures allow us to place a variety of proposed privatization schemes -- some differentially private, some not -- on the same footing. We analyze these measures theoretically under a distributional model which encapsulates reasonable adversarial settings. We also quantify their behavior empirically on real and simulated prediction tasks. Across a range of experimental settings, we find that differentially private schemes dominate or match the privacy-utility tradeoff of more heuristic approaches.

Differentially Private Sampling from Distributions

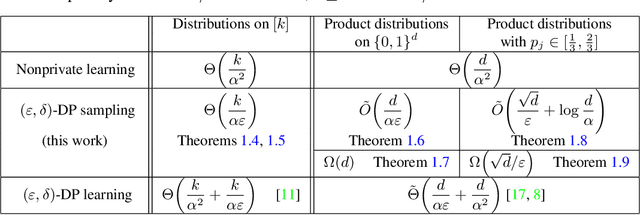
We initiate an investigation of private sampling from distributions. Given a dataset with $n$ independent observations from an unknown distribution $P$, a sampling algorithm must output a single observation from a distribution that is close in total variation distance to $P$ while satisfying differential privacy. Sampling abstracts the goal of generating small amounts of realistic-looking data. We provide tight upper and lower bounds for the dataset size needed for this task for three natural families of distributions: arbitrary distributions on $\{1,\ldots ,k\}$, arbitrary product distributions on $\{0,1\}^d$, and product distributions on $\{0,1\}^d$ with bias in each coordinate bounded away from 0 and 1. We demonstrate that, in some parameter regimes, private sampling requires asymptotically fewer observations than learning a description of $P$ nonprivately; in other regimes, however, private sampling proves to be as difficult as private learning. Notably, for some classes of distributions, the overhead in the number of observations needed for private learning compared to non-private learning is completely captured by the number of observations needed for private sampling.

Improved Differentially Private Analysis of Variance

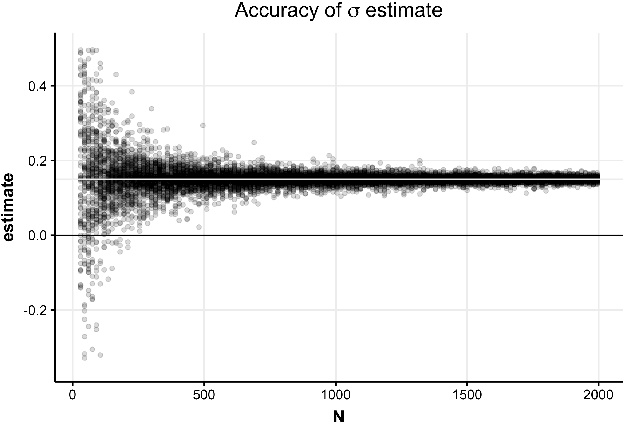
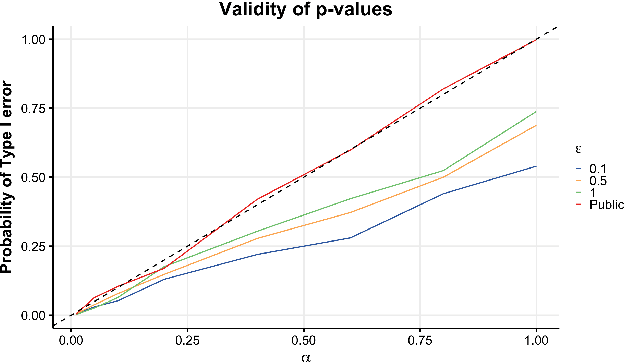
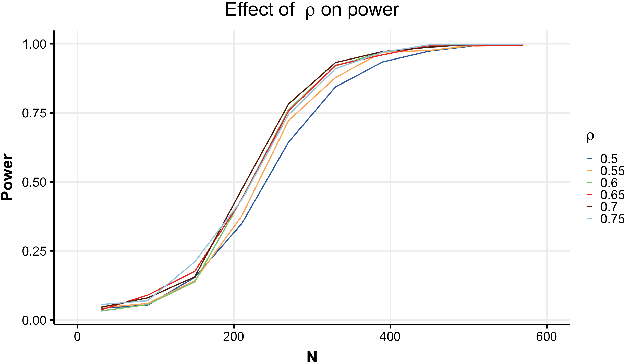
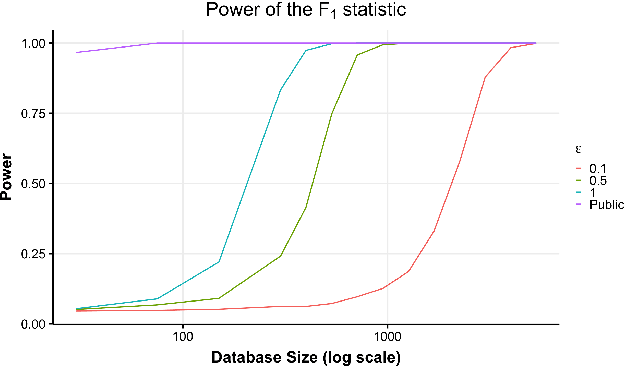
Hypothesis testing is one of the most common types of data analysis and forms the backbone of scientific research in many disciplines. Analysis of variance (ANOVA) in particular is used to detect dependence between a categorical and a numerical variable. Here we show how one can carry out this hypothesis test under the restrictions of differential privacy. We show that the $F$-statistic, the optimal test statistic in the public setting, is no longer optimal in the private setting, and we develop a new test statistic $F_1$ with much higher statistical power. We show how to rigorously compute a reference distribution for the $F_1$ statistic and give an algorithm that outputs accurate $p$-values. We implement our test and experimentally optimize several parameters. We then compare our test to the only previous work on private ANOVA testing, using the same effect size as that work. We see an order of magnitude improvement, with our test requiring only 7% as much data to detect the effect.