Claudio Gentile
IMT
TBDFiltering: Sample-Efficient Tree-Based Data Filtering
Jan 29, 2026Abstract:The quality of machine learning models depends heavily on their training data. Selecting high-quality, diverse training sets for large language models (LLMs) is a difficult task, due to the lack of cheap and reliable quality metrics. While querying existing LLMs for document quality is common, this is not scalable to the large number (billions) of documents used in training. Instead, practitioners often use classifiers trained on sparse quality signals. In this paper, we propose a text-embedding-based hierarchical clustering approach that adaptively selects the documents to be evaluated by the LLM to estimate cluster quality. We prove that our method is query efficient: under the assumption that the hierarchical clustering contains a subtree such that each leaf cluster in the tree is pure enough (i.e., it mostly contains either only good or only bad documents), with high probability, the method can correctly predict the quality of each document after querying a small number of documents. The number of such documents is proportional to the size of the smallest subtree with (almost) pure leaves, without the algorithm knowing this subtree in advance. Furthermore, in a comprehensive experimental study, we demonstrate the benefits of our algorithm compared to other classifier-based filtering methods.
Optimal Learning from Label Proportions with General Loss Functions
Sep 18, 2025



Abstract:Motivated by problems in online advertising, we address the task of Learning from Label Proportions (LLP). In this partially-supervised setting, training data consists of groups of examples, termed bags, for which we only observe the average label value. The main goal, however, remains the design of a predictor for the labels of individual examples. We introduce a novel and versatile low-variance de-biasing methodology to learn from aggregate label information, significantly advancing the state of the art in LLP. Our approach exhibits remarkable flexibility, seamlessly accommodating a broad spectrum of practically relevant loss functions across both binary and multi-class classification settings. By carefully combining our estimators with standard techniques, we substantially improve sample complexity guarantees for a large class of losses of practical relevance. We also empirically validate the efficacy of our proposed approach across a diverse array of benchmark datasets, demonstrating compelling empirical advantages over standard baselines.
Nearly Optimal Sample Complexity for Learning with Label Proportions
May 08, 2025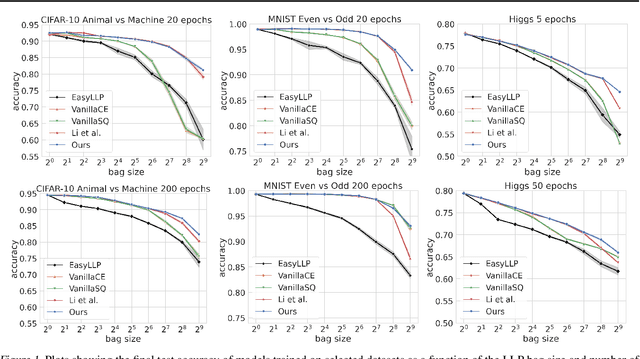
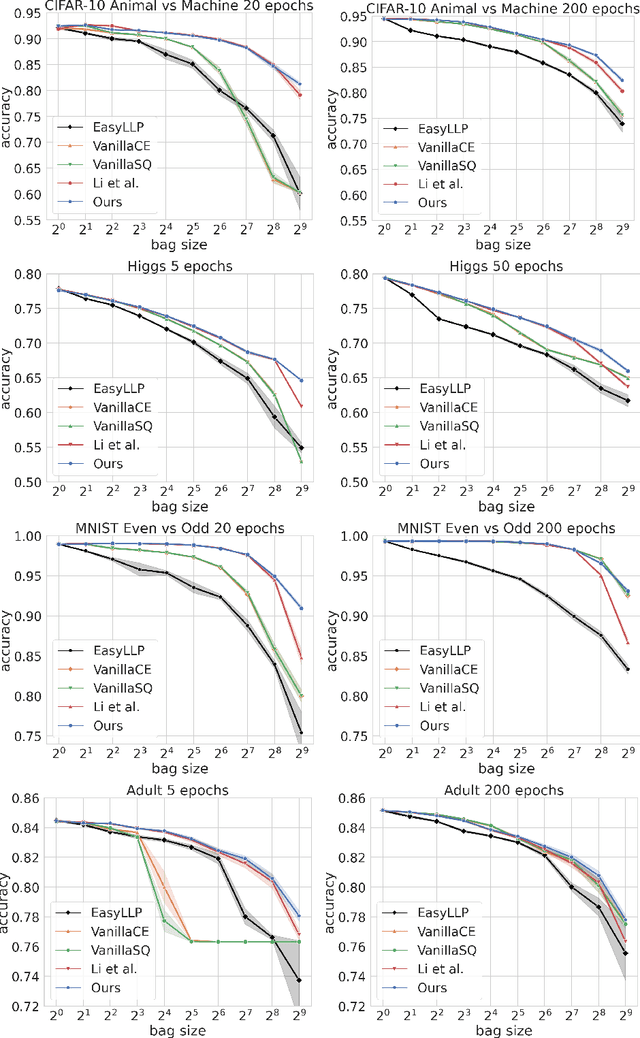
Abstract:We investigate Learning from Label Proportions (LLP), a partial information setting where examples in a training set are grouped into bags, and only aggregate label values in each bag are available. Despite the partial observability, the goal is still to achieve small regret at the level of individual examples. We give results on the sample complexity of LLP under square loss, showing that our sample complexity is essentially optimal. From an algorithmic viewpoint, we rely on carefully designed variants of Empirical Risk Minimization, and Stochastic Gradient Descent algorithms, combined with ad hoc variance reduction techniques. On one hand, our theoretical results improve in important ways on the existing literature on LLP, specifically in the way the sample complexity depends on the bag size. On the other hand, we validate our algorithmic solutions on several datasets, demonstrating improved empirical performance (better accuracy for less samples) against recent baselines.
Auditing Privacy Mechanisms via Label Inference Attacks
Jun 04, 2024



Abstract:We propose reconstruction advantage measures to audit label privatization mechanisms. A reconstruction advantage measure quantifies the increase in an attacker's ability to infer the true label of an unlabeled example when provided with a private version of the labels in a dataset (e.g., aggregate of labels from different users or noisy labels output by randomized response), compared to an attacker that only observes the feature vectors, but may have prior knowledge of the correlation between features and labels. We consider two such auditing measures: one additive, and one multiplicative. These incorporate previous approaches taken in the literature on empirical auditing and differential privacy. The measures allow us to place a variety of proposed privatization schemes -- some differentially private, some not -- on the same footing. We analyze these measures theoretically under a distributional model which encapsulates reasonable adversarial settings. We also quantify their behavior empirically on real and simulated prediction tasks. Across a range of experimental settings, we find that differentially private schemes dominate or match the privacy-utility tradeoff of more heuristic approaches.
Fast and Effective GNN Training with Linearized Random Spanning Trees
Jun 09, 2023


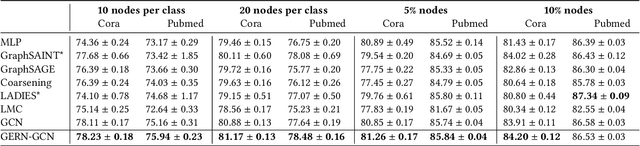
Abstract:We present a new effective and scalable framework for training GNNs in supervised node classification tasks, given graph-structured data. Our approach increasingly refines the weight update operations on a sequence of path graphs obtained by linearizing random spanning trees extracted from the input network. The path graphs are designed to retain essential topological and node information of the original graph. At the same time, the sparsity of path graphs enables a much lighter GNN training which, besides scalability, helps in mitigating classical training issues, like over-squashing and over-smoothing. We carry out an extensive experimental investigation on a number of real-world graph benchmarks, where we apply our framework to graph convolutional networks, showing simultaneous improvement of both training speed and test accuracy, as compared to well-known baselines.
Data-Driven Regret Balancing for Online Model Selection in Bandits
Jun 05, 2023



Abstract:We consider model selection for sequential decision making in stochastic environments with bandit feedback, where a meta-learner has at its disposal a pool of base learners, and decides on the fly which action to take based on the policies recommended by each base learner. Model selection is performed by regret balancing but, unlike the recent literature on this subject, we do not assume any prior knowledge about the base learners like candidate regret guarantees; instead, we uncover these quantities in a data-driven manner. The meta-learner is therefore able to leverage the realized regret incurred by each base learner for the learning environment at hand (as opposed to the expected regret), and single out the best such regret. We design two model selection algorithms operating with this more ambitious notion of regret and, besides proving model selection guarantees via regret balancing, we experimentally demonstrate the compelling practical benefits of dealing with actual regrets instead of candidate regret bounds.
Easy Learning from Label Proportions
Feb 13, 2023



Abstract:We consider the problem of Learning from Label Proportions (LLP), a weakly supervised classification setup where instances are grouped into "bags", and only the frequency of class labels at each bag is available. Albeit, the objective of the learner is to achieve low task loss at an individual instance level. Here we propose Easyllp: a flexible and simple-to-implement debiasing approach based on aggregate labels, which operates on arbitrary loss functions. Our technique allows us to accurately estimate the expected loss of an arbitrary model at an individual level. We showcase the flexibility of our approach by applying it to popular learning frameworks, like Empirical Risk Minimization (ERM) and Stochastic Gradient Descent (SGD) with provable guarantees on instance level performance. More concretely, we exhibit a variance reduction technique that makes the quality of LLP learning deteriorate only by a factor of k (k being bag size) in both ERM and SGD setups, as compared to full supervision. Finally, we validate our theoretical results on multiple datasets demonstrating our algorithm performs as well or better than previous LLP approaches in spite of its simplicity.
Regret Guarantees for Adversarial Online Collaborative Filtering
Feb 11, 2023



Abstract:We investigate the problem of online collaborative filtering under no-repetition constraints, whereby users need to be served content in an online fashion and a given user cannot be recommended the same content item more than once. We design and analyze a fully adaptive algorithm that works under biclustering assumptions on the user-item preference matrix, and show that this algorithm exhibits an optimal regret guarantee, while being oblivious to any prior knowledge about the sequence of users, the universe of items, as well as the biclustering parameters of the preference matrix. We further propose a more robust version of the algorithm which addresses the scenario when the preference matrix is adversarially perturbed. We then give regret guarantees that scale with the amount by which the preference matrix is perturbed from a biclustered structure. To our knowledge, these are the first results on online collaborative filtering that hold at this level of generality and adaptivity under no-repetition constraints.
Leveraging User-Triggered Supervision in Contextual Bandits
Feb 07, 2023Abstract:We study contextual bandit (CB) problems, where the user can sometimes respond with the best action in a given context. Such an interaction arises, for example, in text prediction or autocompletion settings, where a poor suggestion is simply ignored and the user enters the desired text instead. Crucially, this extra feedback is user-triggered on only a subset of the contexts. We develop a new framework to leverage such signals, while being robust to their biased nature. We also augment standard CB algorithms to leverage the signal, and show improved regret guarantees for the resulting algorithms under a variety of conditions on the helpfulness of and bias inherent in this feedback.
A Contextual Bandit Approach for Learning to Plan in Environments with Probabilistic Goal Configurations
Nov 29, 2022



Abstract:Object-goal navigation (Object-nav) entails searching, recognizing and navigating to a target object. Object-nav has been extensively studied by the Embodied-AI community, but most solutions are often restricted to considering static objects (e.g., television, fridge, etc.). We propose a modular framework for object-nav that is able to efficiently search indoor environments for not just static objects but also movable objects (e.g. fruits, glasses, phones, etc.) that frequently change their positions due to human intervention. Our contextual-bandit agent efficiently explores the environment by showing optimism in the face of uncertainty and learns a model of the likelihood of spotting different objects from each navigable location. The likelihoods are used as rewards in a weighted minimum latency solver to deduce a trajectory for the robot. We evaluate our algorithms in two simulated environments and a real-world setting, to demonstrate high sample efficiency and reliability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge