Self-Directed Learning of Convex Labelings on Graphs

We study the problem of learning the clusters of a given graph in the self-directed learning setup. This learning setting is a variant of online learning, where rather than an adversary determining the sequence in which nodes are presented, the learner autonomously and adaptively selects them. While self-directed learning of Euclidean halfspaces, linear functions, and general abstract multi-class hypothesis classes was recently considered, no results previously existed specifically for self-directed node classification on graphs. In this paper, we address this problem developing efficient algorithms for it. More specifically, we focus on the case of (geodesically) convex clusters, i.e., for every two nodes sharing the same label, all nodes on every shortest path between them also share the same label. In particular, we devise a polynomial-time algorithm that makes only $3(h(G)+1)^4 \ln n$ mistakes on graphs with two convex clusters, where $n$ is the total number of nodes and $h(G)$ is the Hadwiger number, i.e., the size of the largest clique minor of the graph $G$. We also show that our algorithm is robust to the case that clusters are slightly non-convex, still achieving a mistake bound logarithmic in $n$. Finally, for the more standard case of homophilic clusters, where strongly connected nodes tend to belong the same class, we devise a simple and efficient algorithm.

Bandits with Abstention under Expert Advice

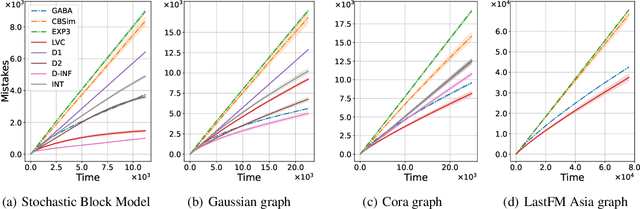
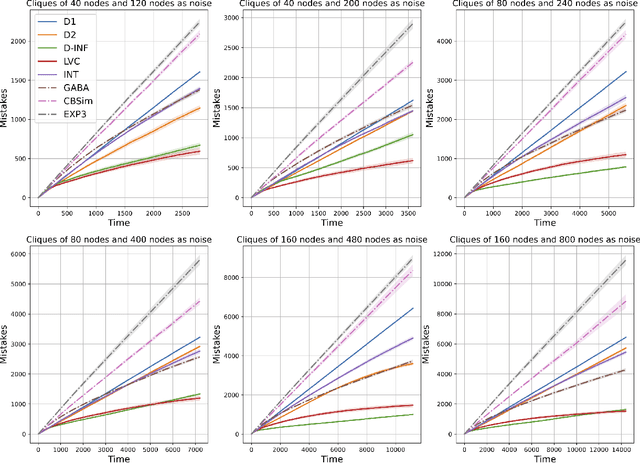
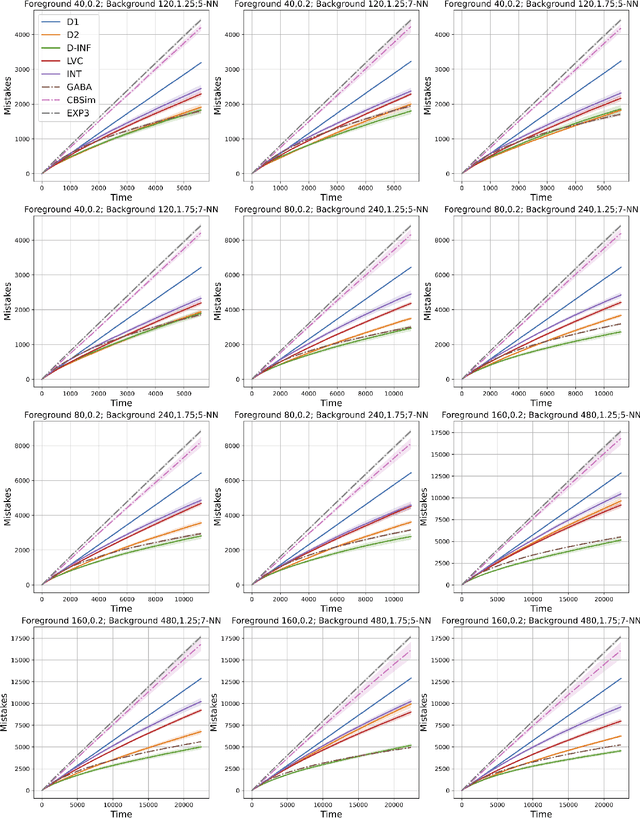
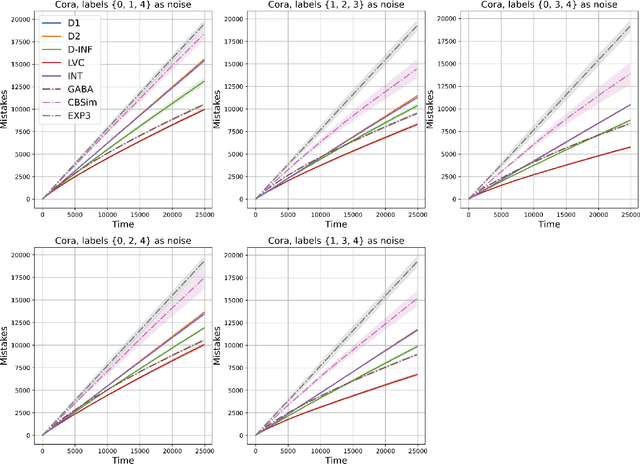
We study the classic problem of prediction with expert advice under bandit feedback. Our model assumes that one action, corresponding to the learner's abstention from play, has no reward or loss on every trial. We propose the CBA algorithm, which exploits this assumption to obtain reward bounds that can significantly improve those of the classical Exp4 algorithm. We can view our problem as the aggregation of confidence-rated predictors when the learner has the option of abstention from play. Importantly, we are the first to achieve bounds on the expected cumulative reward for general confidence-rated predictors. In the special case of specialists we achieve a novel reward bound, significantly improving previous bounds of SpecialistExp (treating abstention as another action). As an example application, we discuss learning unions of balls in a finite metric space. In this contextual setting, we devise an efficient implementation of CBA, reducing the runtime from quadratic to almost linear in the number of contexts. Preliminary experiments show that CBA improves over existing bandit algorithms.

Best-of-Both-Worlds Algorithms for Linear Contextual Bandits

We study best-of-both-worlds algorithms for $K$-armed linear contextual bandits. Our algorithms deliver near-optimal regret bounds in both the adversarial and stochastic regimes, without prior knowledge about the environment. In the stochastic regime, we achieve the polylogarithmic rate $\frac{(dK)^2\mathrm{poly}\log(dKT)}{\Delta_{\min}}$, where $\Delta_{\min}$ is the minimum suboptimality gap over the $d$-dimensional context space. In the adversarial regime, we obtain either the first-order $\widetilde{O}(dK\sqrt{L^*})$ bound, or the second-order $\widetilde{O}(dK\sqrt{\Lambda^*})$ bound, where $L^*$ is the cumulative loss of the best action and $\Lambda^*$ is a notion of the cumulative second moment for the losses incurred by the algorithm. Moreover, we develop an algorithm based on FTRL with Shannon entropy regularizer that does not require the knowledge of the inverse of the covariance matrix, and achieves a polylogarithmic regret in the stochastic regime while obtaining $\widetilde{O}\big(dK\sqrt{T}\big)$ regret bounds in the adversarial regime.

Sum-max Submodular Bandits

Many online decision-making problems correspond to maximizing a sequence of submodular functions. In this work, we introduce sum-max functions, a subclass of monotone submodular functions capturing several interesting problems, including best-of-$K$-bandits, combinatorial bandits, and the bandit versions on facility location, $M$-medians, and hitting sets. We show that all functions in this class satisfy a key property that we call pseudo-concavity. This allows us to prove $\big(1 - \frac{1}{e}\big)$-regret bounds for bandit feedback in the nonstochastic setting of the order of $\sqrt{MKT}$ (ignoring log factors), where $T$ is the time horizon and $M$ is a cardinality constraint. This bound, attained by a simple and efficient algorithm, significantly improves on the $\widetilde{O}\big(T^{2/3}\big)$ regret bound for online monotone submodular maximization with bandit feedback.

Fast and Effective GNN Training with Linearized Random Spanning Trees

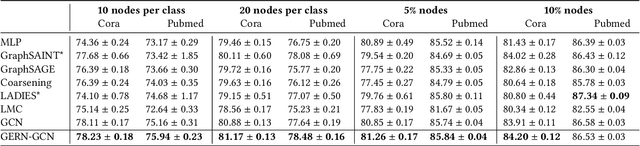
We present a new effective and scalable framework for training GNNs in supervised node classification tasks, given graph-structured data. Our approach increasingly refines the weight update operations on a sequence of path graphs obtained by linearizing random spanning trees extracted from the input network. The path graphs are designed to retain essential topological and node information of the original graph. At the same time, the sparsity of path graphs enables a much lighter GNN training which, besides scalability, helps in mitigating classical training issues, like over-squashing and over-smoothing. We carry out an extensive experimental investigation on a number of real-world graph benchmarks, where we apply our framework to graph convolutional networks, showing simultaneous improvement of both training speed and test accuracy, as compared to well-known baselines.

Regret Guarantees for Adversarial Online Collaborative Filtering

We investigate the problem of online collaborative filtering under no-repetition constraints, whereby users need to be served content in an online fashion and a given user cannot be recommended the same content item more than once. We design and analyze a fully adaptive algorithm that works under biclustering assumptions on the user-item preference matrix, and show that this algorithm exhibits an optimal regret guarantee, while being oblivious to any prior knowledge about the sequence of users, the universe of items, as well as the biclustering parameters of the preference matrix. We further propose a more robust version of the algorithm which addresses the scenario when the preference matrix is adversarially perturbed. We then give regret guarantees that scale with the amount by which the preference matrix is perturbed from a biclustered structure. To our knowledge, these are the first results on online collaborative filtering that hold at this level of generality and adaptivity under no-repetition constraints.

Online Learning of Facility Locations

In this paper, we provide a rigorous theoretical investigation of an online learning version of the Facility Location problem which is motivated by emerging problems in real-world applications. In our formulation, we are given a set of sites and an online sequence of user requests. At each trial, the learner selects a subset of sites and then incurs a cost for each selected site and an additional cost which is the price of the user's connection to the nearest site in the selected subset. The problem may be solved by an application of the well-known Hedge algorithm. This would, however, require time and space exponential in the number of the given sites, which motivates our design of a novel quasi-linear time algorithm for this problem, with good theoretical guarantees on its performance.

Flattening a Hierarchical Clustering through Active Learning

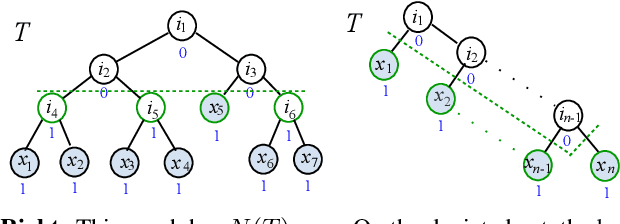
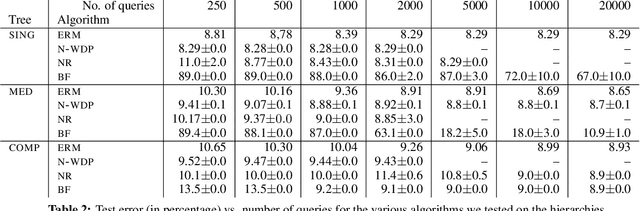
We investigate active learning by pairwise similarity over the leaves of trees originating from hierarchical clustering procedures. In the realizable setting, we provide a full characterization of the number of queries needed to achieve perfect reconstruction of the tree cut. In the non-realizable setting, we rely on known important-sampling procedures to obtain regret and query complexity bounds. Our algorithms come with theoretical guarantees on the statistical error and, more importantly, lend themselves to linear-time implementations in the relevant parameters of the problem. We discuss such implementations, prove running time guarantees for them, and present preliminary experiments on real-world datasets showing the compelling practical performance of our algorithms as compared to both passive learning and simple active learning baselines.

Correlation Clustering with Adaptive Similarity Queries

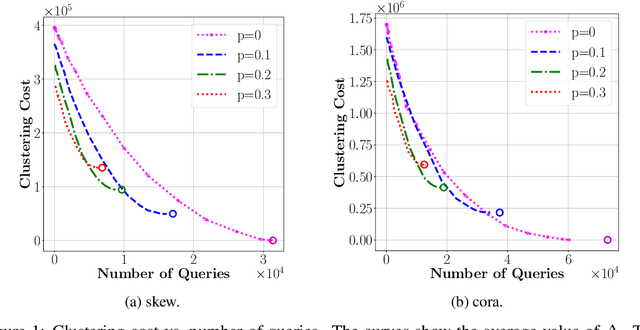
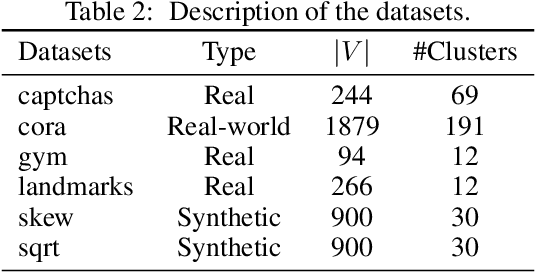
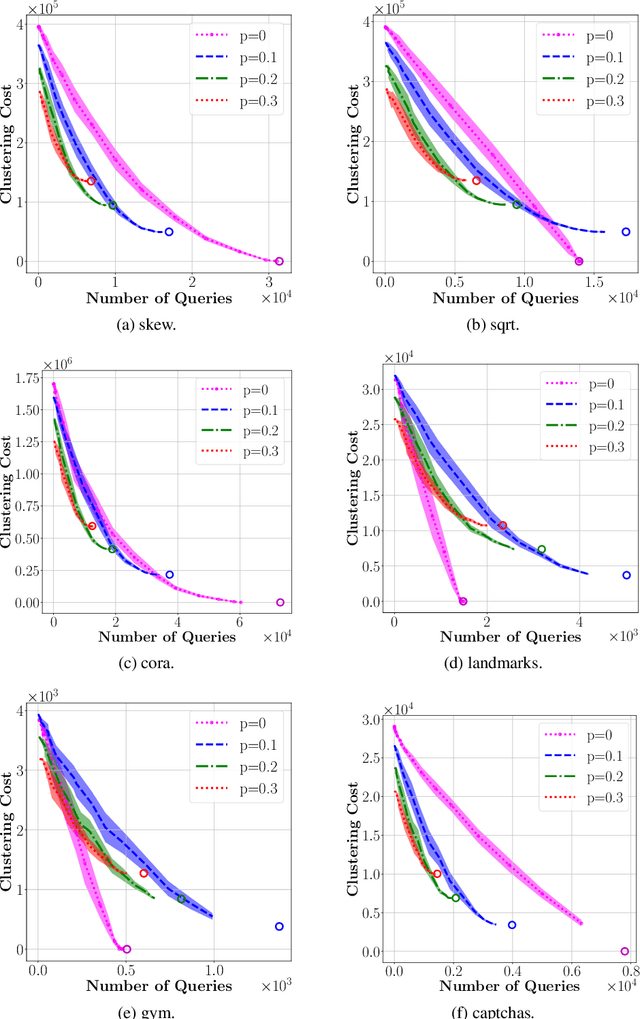
We investigate learning algorithms that use similarity queries to approximately solve correlation clustering problems. The input consists of $n$ objects; each pair of objects has a hidden binary similarity score that we can learn through a query. The goal is to use as few queries as possible to partition the objects into clusters so to achieve the optimal number OPT of disagreements with the scores. Our first set of contributions is algorithmic: we introduce ACC, a simple query-aware variant of an existing algorithm (KwikCluster, with expected error 3OPT but a vacuous $\mathcal{O}(n^2)$ worst-case bound on the number of queries) for which we prove several desirable properties. First, ACC has expected error 3OPT$ + \mathcal{O}(n^3/Q)$ when using $Q < \binom{n}{2}$ queries, and recovers KwikCluster's bound of 3OPT for $Q=\binom{n}{2}$. Second, ACC accurately recovers every adversarially perturbed latent cluster $C$. Under stronger conditions on $C$, ACC can even be used to recover exactly all clusters with high probability. Third, we show an efficient variant, \aggress, with the same expected error as ACC but using significantly less queries on some graphs. We empirically test our algorithms on real-world and synthetic datasets. Our second set of contributions is a nearly complete information-theoretic characterization of the query vs.\ error trade-off. First, using VC theory, for all $Q = \Omega(n)$ we prove the existence of algorithms with expected error at most OPT$+ n^{5/2}/\sqrt{Q}$, and at most $\widetilde{\mathcal{O}}\big(n^3/Q\big)$ if OPT=0. We then show that any randomized algorithm, when using at most $Q$ queries, must output a clustering with expected cost OPT$+ \Omega\big(n^3/Q\big)$, which matches the upper bound for $Q=\Theta(n)$. For the special case of OPT=0 we prove a weaker lower bound of $\Omega\big(n^2/\sqrt{Q}\big)$.

MaxHedge: Maximising a Maximum Online with Theoretical Performance Guarantees

We introduce a new online learning framework where, at each trial, the learner is required to select a subset of actions from a given known action set. Each action is associated with an energy value, a reward and a cost. The sum of the energies of the actions selected cannot exceed a given energy budget. The goal is to maximise the cumulative profit, where the profit obtained on a single trial is defined as the difference between the maximum reward among the selected actions and the sum of their costs. Action energy values and the budget are known and fixed. All rewards and costs associated with each action change over time and are revealed at each trial only after the learner's selection of actions. Our framework encompasses several online learning problems where the environment changes over time; and the solution trades-off between minimising the costs and maximising the maximum reward of the selected subset of actions, while being constrained to an action energy budget. The algorithm that we propose is an efficient and very scalable unifying approach which is capable of solving our general problem. Hence, our method solves several online learning problems which fall into this general framework.