Of Dice and Games: A Theory of Generalized Boosting

Cost-sensitive loss functions are crucial in many real-world prediction problems, where different types of errors are penalized differently; for example, in medical diagnosis, a false negative prediction can lead to worse consequences than a false positive prediction. However, traditional PAC learning theory has mostly focused on the symmetric 0-1 loss, leaving cost-sensitive losses largely unaddressed. In this work, we extend the celebrated theory of boosting to incorporate both cost-sensitive and multi-objective losses. Cost-sensitive losses assign costs to the entries of a confusion matrix, and are used to control the sum of prediction errors accounting for the cost of each error type. Multi-objective losses, on the other hand, simultaneously track multiple cost-sensitive losses, and are useful when the goal is to satisfy several criteria at once (e.g., minimizing false positives while keeping false negatives below a critical threshold). We develop a comprehensive theory of cost-sensitive and multi-objective boosting, providing a taxonomy of weak learning guarantees that distinguishes which guarantees are trivial (i.e., can always be achieved), which ones are boostable (i.e., imply strong learning), and which ones are intermediate, implying non-trivial yet not arbitrarily accurate learning. For binary classification, we establish a dichotomy: a weak learning guarantee is either trivial or boostable. In the multiclass setting, we describe a more intricate landscape of intermediate weak learning guarantees. Our characterization relies on a geometric interpretation of boosting, revealing a surprising equivalence between cost-sensitive and multi-objective losses.

A Theory of Interpretable Approximations

Can a deep neural network be approximated by a small decision tree based on simple features? This question and its variants are behind the growing demand for machine learning models that are *interpretable* by humans. In this work we study such questions by introducing *interpretable approximations*, a notion that captures the idea of approximating a target concept $c$ by a small aggregation of concepts from some base class $\mathcal{H}$. In particular, we consider the approximation of a binary concept $c$ by decision trees based on a simple class $\mathcal{H}$ (e.g., of bounded VC dimension), and use the tree depth as a measure of complexity. Our primary contribution is the following remarkable trichotomy. For any given pair of $\mathcal{H}$ and $c$, exactly one of these cases holds: (i) $c$ cannot be approximated by $\mathcal{H}$ with arbitrary accuracy; (ii) $c$ can be approximated by $\mathcal{H}$ with arbitrary accuracy, but there exists no universal rate that bounds the complexity of the approximations as a function of the accuracy; or (iii) there exists a constant $\kappa$ that depends only on $\mathcal{H}$ and $c$ such that, for *any* data distribution and *any* desired accuracy level, $c$ can be approximated by $\mathcal{H}$ with a complexity not exceeding $\kappa$. This taxonomy stands in stark contrast to the landscape of supervised classification, which offers a complex array of distribution-free and universally learnable scenarios. We show that, in the case of interpretable approximations, even a slightly nontrivial a-priori guarantee on the complexity of approximations implies approximations with constant (distribution-free and accuracy-free) complexity. We extend our trichotomy to classes $\mathcal{H}$ of unbounded VC dimension and give characterizations of interpretability based on the algebra generated by $\mathcal{H}$.

Efficient Algorithms for Learning Monophonic Halfspaces in Graphs

We study the problem of learning a binary classifier on the vertices of a graph. In particular, we consider classifiers given by monophonic halfspaces, partitions of the vertices that are convex in a certain abstract sense. Monophonic halfspaces, and related notions such as geodesic halfspaces,have recently attracted interest, and several connections have been drawn between their properties(e.g., their VC dimension) and the structure of the underlying graph $G$. We prove several novel results for learning monophonic halfspaces in the supervised, online, and active settings. Our main result is that a monophonic halfspace can be learned with near-optimal passive sample complexity in time polynomial in $n = |V(G)|$. This requires us to devise a polynomial-time algorithm for consistent hypothesis checking, based on several structural insights on monophonic halfspaces and on a reduction to $2$-satisfiability. We prove similar results for the online and active settings. We also show that the concept class can be enumerated with delay $\operatorname{poly}(n)$, and that empirical risk minimization can be performed in time $2^{\omega(G)}\operatorname{poly}(n)$ where $\omega(G)$ is the clique number of $G$. These results answer open questions from the literature (Gonz\'alez et al., 2020), and show a contrast with geodesic halfspaces, for which some of the said problems are NP-hard (Seiffarth et al., 2023).

Fully-Dynamic Approximate Decision Trees With Worst-Case Update Time Guarantees

We give the first algorithm that maintains an approximate decision tree over an arbitrary sequence of insertions and deletions of labeled examples, with strong guarantees on the worst-case running time per update request. For instance, we show how to maintain a decision tree where every vertex has Gini gain within an additive $\alpha$ of the optimum by performing $O\Big(\frac{d\,(\log n)^4}{\alpha^3}\Big)$ elementary operations per update, where $d$ is the number of features and $n$ the maximum size of the active set (the net result of the update requests). We give similar bounds for the information gain and the variance gain. In fact, all these bounds are corollaries of a more general result, stated in terms of decision rules -- functions that, given a set $S$ of labeled examples, decide whether to split $S$ or predict a label. Decision rules give a unified view of greedy decision tree algorithms regardless of the example and label domains, and lead to a general notion of $\epsilon$-approximate decision trees that, for natural decision rules such as those used by ID3 or C4.5, implies the gain approximation guarantees above. The heart of our work provides a deterministic algorithm that, given any decision rule and any $\epsilon > 0$, maintains an $\epsilon$-approximate tree using $O\!\left(\frac{d\, f(n)}{n} \operatorname{poly}\frac{h}{\epsilon}\right)$ operations per update, where $f(n)$ is the complexity of evaluating the rule over a set of $n$ examples and $h$ is the maximum height of the maintained tree.

Fully-Dynamic Decision Trees

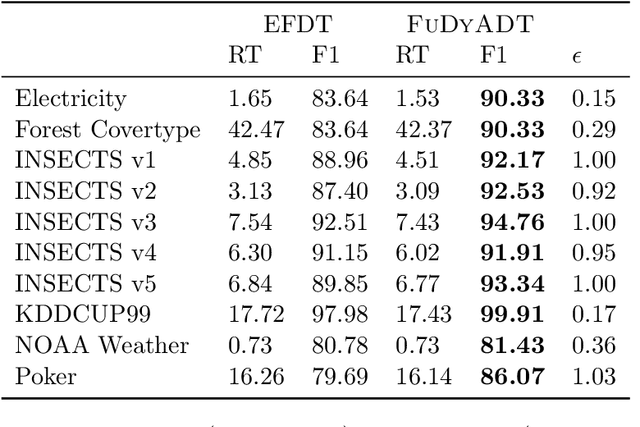
We develop the first fully dynamic algorithm that maintains a decision tree over an arbitrary sequence of insertions and deletions of labeled examples. Given $\epsilon > 0$ our algorithm guarantees that, at every point in time, every node of the decision tree uses a split with Gini gain within an additive $\epsilon$ of the optimum. For real-valued features the algorithm has an amortized running time per insertion/deletion of $O\big(\frac{d \log^3 n}{\epsilon^2}\big)$, which improves to $O\big(\frac{d \log^2 n}{\epsilon}\big)$ for binary or categorical features, while it uses space $O(n d)$, where $n$ is the maximum number of examples at any point in time and $d$ is the number of features. Our algorithm is nearly optimal, as we show that any algorithm with similar guarantees uses amortized running time $\Omega(d)$ and space $\tilde{\Omega} (n d)$. We complement our theoretical results with an extensive experimental evaluation on real-world data, showing the effectiveness of our algorithm.

Active Learning of Classifiers with Label and Seed Queries

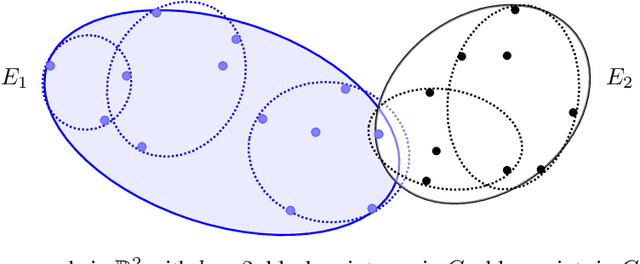
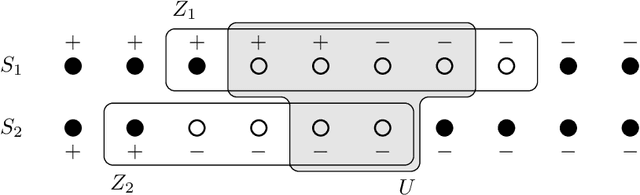
We study exact active learning of binary and multiclass classifiers with margin. Given an $n$-point set $X \subset \mathbb{R}^m$, we want to learn any unknown classifier on $X$ whose classes have finite strong convex hull margin, a new notion extending the SVM margin. In the standard active learning setting, where only label queries are allowed, learning a classifier with strong convex hull margin $\gamma$ requires in the worst case $\Omega\big(1+\frac{1}{\gamma}\big)^{(m-1)/2}$ queries. On the other hand, using the more powerful seed queries (a variant of equivalence queries), the target classifier could be learned in $O(m \log n)$ queries via Littlestone's Halving algorithm; however, Halving is computationally inefficient. In this work we show that, by carefully combining the two types of queries, a binary classifier can be learned in time $\operatorname{poly}(n+m)$ using only $O(m^2 \log n)$ label queries and $O\big(m \log \frac{m}{\gamma}\big)$ seed queries; the result extends to $k$-class classifiers at the price of a $k!k^2$ multiplicative overhead. Similar results hold when the input points have bounded bit complexity, or when only one class has strong convex hull margin against the rest. We complement the upper bounds by showing that in the worst case any algorithm needs $\Omega\big(k m \log \frac{1}{\gamma}\big)$ seed and label queries to learn a $k$-class classifier with strong convex hull margin $\gamma$.

On Margin-Based Cluster Recovery with Oracle Queries

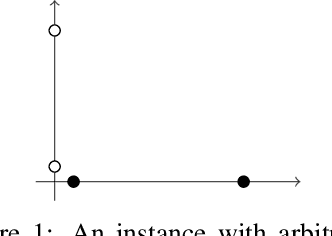
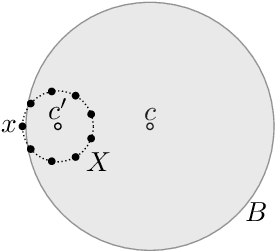
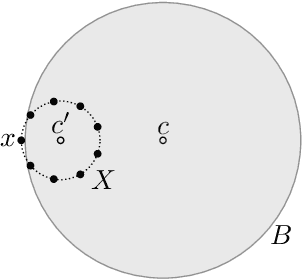
We study an active cluster recovery problem where, given a set of $n$ points and an oracle answering queries like "are these two points in the same cluster?", the task is to recover exactly all clusters using as few queries as possible. We begin by introducing a simple but general notion of margin between clusters that captures, as special cases, the margins used in previous work, the classic SVM margin, and standard notions of stability for center-based clusterings. Then, under our margin assumptions we design algorithms that, in a variety of settings, recover all clusters exactly using only $O(\log n)$ queries. For the Euclidean case, $\mathbb{R}^m$, we give an algorithm that recovers arbitrary convex clusters, in polynomial time, and with a number of queries that is lower than the best existing algorithm by $\Theta(m^m)$ factors. For general pseudometric spaces, where clusters might not be convex or might not have any notion of shape, we give an algorithm that achieves the $O(\log n)$ query bound, and is provably near-optimal as a function of the packing number of the space. Finally, for clusterings realized by binary concept classes, we give a combinatorial characterization of recoverability with $O(\log n)$ queries, and we show that, for many concept classes in Euclidean spaces, this characterization is equivalent to our margin condition. Our results show a deep connection between cluster margins and active cluster recoverability.

Exact Recovery of Clusters in Finite Metric Spaces Using Oracle Queries

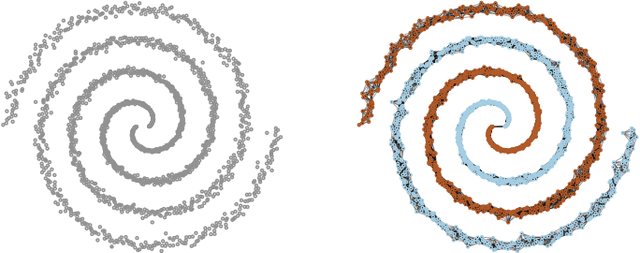
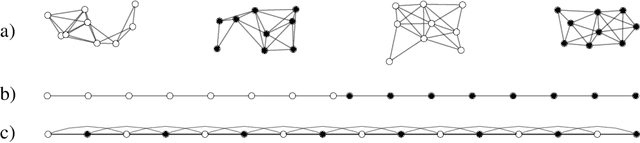
We investigate the problem of exact cluster recovery using oracle queries. Previous results show that clusters in Euclidean spaces that are convex and separated with a margin can be reconstructed exactly using only $O(\log n)$ same-cluster queries, where $n$ is the number of input points. In this work, we study this problem in the more challenging non-convex setting. We introduce a structural characterization of clusters, called $(\beta,\gamma)$-convexity, that can be applied to any finite set of points equipped with a metric (or even a semimetric, as the triangle inequality is not needed). Using $(\beta,\gamma)$-convexity, we can translate natural density properties of clusters (which include, for instance, clusters that are strongly non-convex in $R^d$) into a graph-theoretic notion of convexity. By exploiting this convexity notion, we design a deterministic algorithm that recovers $(\beta,\gamma)$-convex clusters using $O(k^2 \log n + k^2 (\frac{6}{\beta\gamma})^{dens(X)})$ same-cluster queries, where $k$ is the number of clusters and $dens(X)$ is the density dimension of the semimetric. We show that an exponential dependence on the density dimension is necessary, and we also show that, if we are allowed to make $O(k^2 + k \log n)$ additional queries to a "cluster separation" oracle, then we can recover clusters that have different and arbitrary scales, even when the scale of each cluster is unknown.

Exact Recovery of Mangled Clusters with Same-Cluster Queries

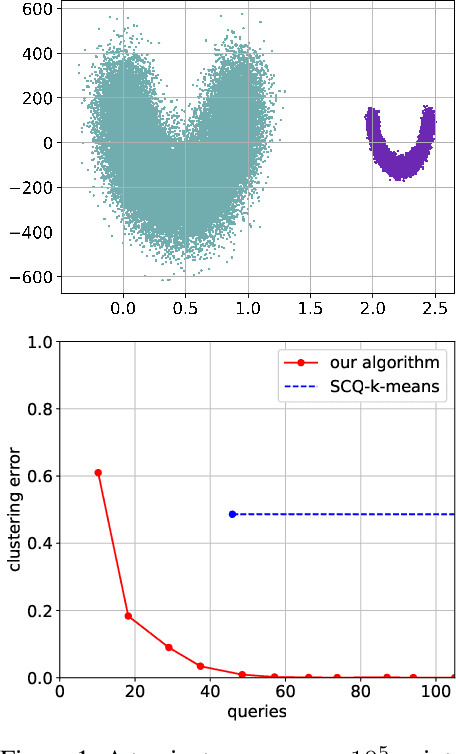
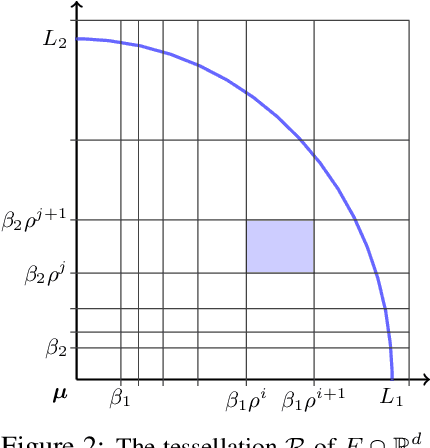
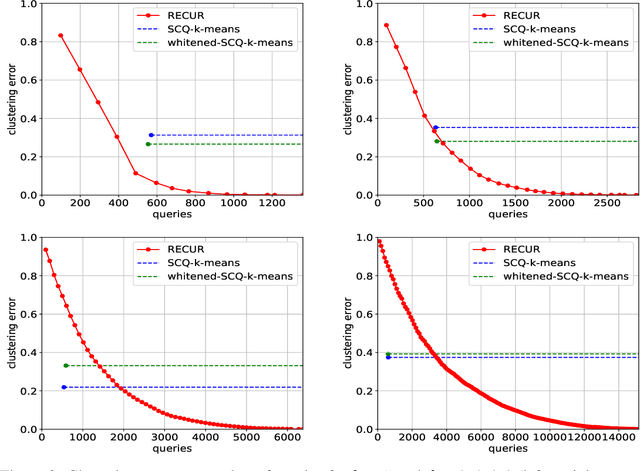
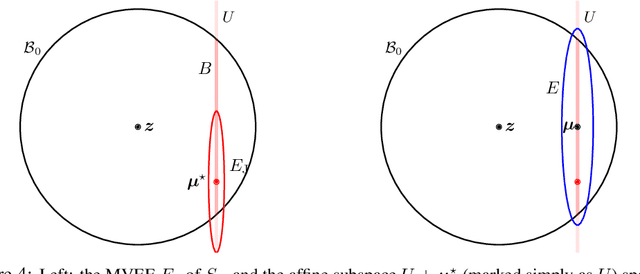
We study the problem of recovering distorted clusters in the semi-supervised active clustering framework. Given an oracle revealing whether any two points lie in the same cluster, we are interested in designing algorithms that recover all clusters exactly, in polynomial time, and using as few queries as possible. Towards this end, we extend the notion of center-based clustering with margin introduced by Ashtiani et al.\ to clusters with arbitrary linear distortions and arbitrary centers. This includes all those cases where the original dataset is transformed by any combination of rotations, axis scalings, and point deletions. We show that, even in this significantly more challenging setting, it is possible to recover the underlying clustering exactly while using only a small number of oracle queries. To this end we design an algorithm that, given $n$ points to be partitioned into $k$ clusters, uses $O(k^3 \ln k \ln n)$ oracle queries and $\tilde{O}(kn + k^3)$ time to recover the exact clustering structure of the underlying instance (even when the instance is NP-hard to solve without oracle access). The $O(\cdot)$ notation hides an exponential dependence on the dimensionality of the clusters, which we show to be necessary. Our algorithm is simple, easy to implement, and can also learn the clusters using low-stretch separators, a class of ellipsoids with additional theoretical guarantees. Experiments on large synthetic datasets confirm that we can reconstruct the latent clustering exactly and efficiently.

Correlation Clustering with Adaptive Similarity Queries

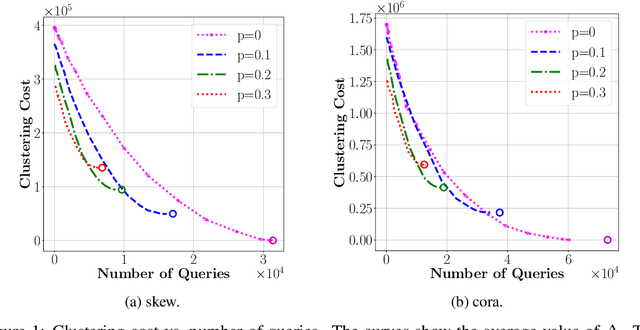
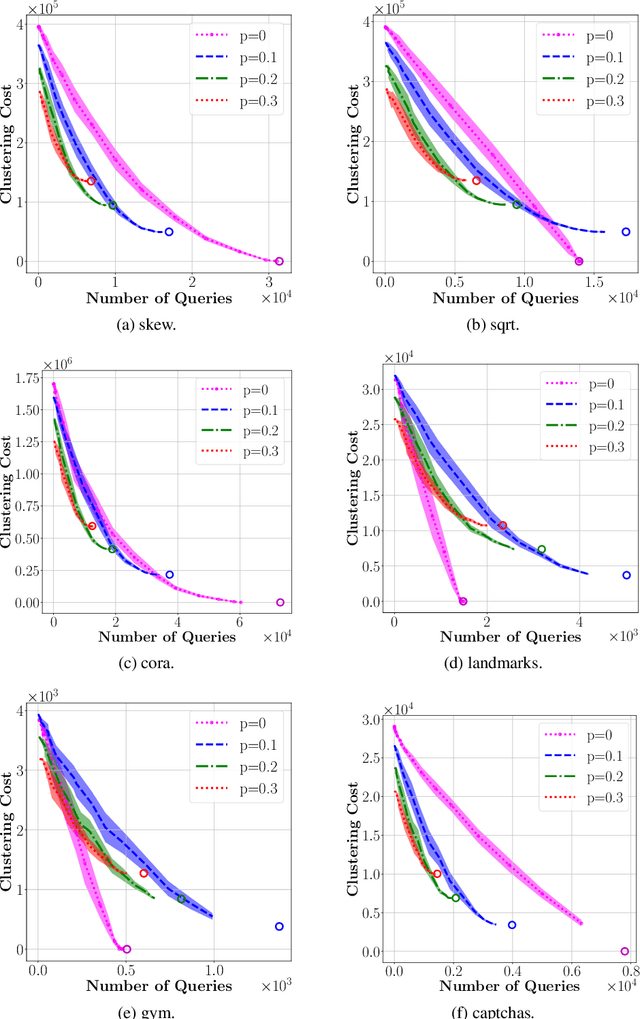
We investigate learning algorithms that use similarity queries to approximately solve correlation clustering problems. The input consists of $n$ objects; each pair of objects has a hidden binary similarity score that we can learn through a query. The goal is to use as few queries as possible to partition the objects into clusters so to achieve the optimal number OPT of disagreements with the scores. Our first set of contributions is algorithmic: we introduce ACC, a simple query-aware variant of an existing algorithm (KwikCluster, with expected error 3OPT but a vacuous $\mathcal{O}(n^2)$ worst-case bound on the number of queries) for which we prove several desirable properties. First, ACC has expected error 3OPT$ + \mathcal{O}(n^3/Q)$ when using $Q < \binom{n}{2}$ queries, and recovers KwikCluster's bound of 3OPT for $Q=\binom{n}{2}$. Second, ACC accurately recovers every adversarially perturbed latent cluster $C$. Under stronger conditions on $C$, ACC can even be used to recover exactly all clusters with high probability. Third, we show an efficient variant, \aggress, with the same expected error as ACC but using significantly less queries on some graphs. We empirically test our algorithms on real-world and synthetic datasets. Our second set of contributions is a nearly complete information-theoretic characterization of the query vs.\ error trade-off. First, using VC theory, for all $Q = \Omega(n)$ we prove the existence of algorithms with expected error at most OPT$+ n^{5/2}/\sqrt{Q}$, and at most $\widetilde{\mathcal{O}}\big(n^3/Q\big)$ if OPT=0. We then show that any randomized algorithm, when using at most $Q$ queries, must output a clustering with expected cost OPT$+ \Omega\big(n^3/Q\big)$, which matches the upper bound for $Q=\Theta(n)$. For the special case of OPT=0 we prove a weaker lower bound of $\Omega\big(n^2/\sqrt{Q}\big)$.