Mauro Sozio
Fully-Dynamic Approximate Decision Trees With Worst-Case Update Time Guarantees
Feb 10, 2023Abstract:We give the first algorithm that maintains an approximate decision tree over an arbitrary sequence of insertions and deletions of labeled examples, with strong guarantees on the worst-case running time per update request. For instance, we show how to maintain a decision tree where every vertex has Gini gain within an additive $\alpha$ of the optimum by performing $O\Big(\frac{d\,(\log n)^4}{\alpha^3}\Big)$ elementary operations per update, where $d$ is the number of features and $n$ the maximum size of the active set (the net result of the update requests). We give similar bounds for the information gain and the variance gain. In fact, all these bounds are corollaries of a more general result, stated in terms of decision rules -- functions that, given a set $S$ of labeled examples, decide whether to split $S$ or predict a label. Decision rules give a unified view of greedy decision tree algorithms regardless of the example and label domains, and lead to a general notion of $\epsilon$-approximate decision trees that, for natural decision rules such as those used by ID3 or C4.5, implies the gain approximation guarantees above. The heart of our work provides a deterministic algorithm that, given any decision rule and any $\epsilon > 0$, maintains an $\epsilon$-approximate tree using $O\!\left(\frac{d\, f(n)}{n} \operatorname{poly}\frac{h}{\epsilon}\right)$ operations per update, where $f(n)$ is the complexity of evaluating the rule over a set of $n$ examples and $h$ is the maximum height of the maintained tree.
Fully-Dynamic Decision Trees
Dec 01, 2022

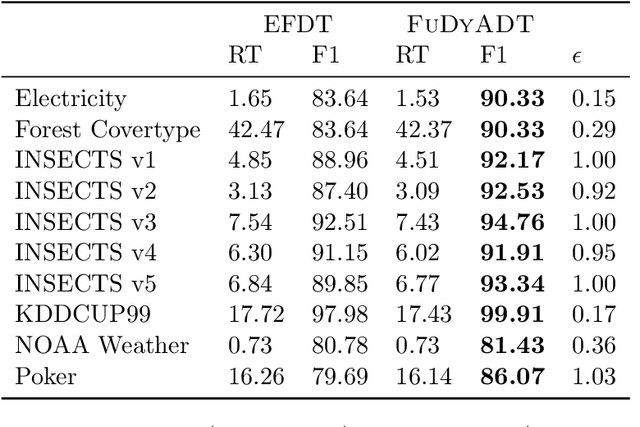

Abstract:We develop the first fully dynamic algorithm that maintains a decision tree over an arbitrary sequence of insertions and deletions of labeled examples. Given $\epsilon > 0$ our algorithm guarantees that, at every point in time, every node of the decision tree uses a split with Gini gain within an additive $\epsilon$ of the optimum. For real-valued features the algorithm has an amortized running time per insertion/deletion of $O\big(\frac{d \log^3 n}{\epsilon^2}\big)$, which improves to $O\big(\frac{d \log^2 n}{\epsilon}\big)$ for binary or categorical features, while it uses space $O(n d)$, where $n$ is the maximum number of examples at any point in time and $d$ is the number of features. Our algorithm is nearly optimal, as we show that any algorithm with similar guarantees uses amortized running time $\Omega(d)$ and space $\tilde{\Omega} (n d)$. We complement our theoretical results with an extensive experimental evaluation on real-world data, showing the effectiveness of our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge