Learning Conditional Averages

We introduce the problem of learning conditional averages in the PAC framework. The learner receives a sample labeled by an unknown target concept from a known concept class, as in standard PAC learning. However, instead of learning the target concept itself, the goal is to predict, for each instance, the average label over its neighborhood -- an arbitrary subset of points that contains the instance. In the degenerate case where all neighborhoods are singletons, the problem reduces exactly to classic PAC learning. More generally, it extends PAC learning to a setting that captures learning tasks arising in several domains, including explainability, fairness, and recommendation systems. Our main contribution is a complete characterization of when conditional averages are learnable, together with sample complexity bounds that are tight up to logarithmic factors. The characterization hinges on the joint finiteness of two novel combinatorial parameters, which depend on both the concept class and the neighborhood system, and are closely related to the independence number of the associated neighborhood graph.

Parameter-free Dynamic Regret: Time-varying Movement Costs, Delayed Feedback, and Memory

In this paper, we study dynamic regret in unconstrained online convex optimization (OCO) with movement costs. Specifically, we generalize the standard setting by allowing the movement cost coefficients $λ_t$ to vary arbitrarily over time. Our main contribution is a novel algorithm that establishes the first comparator-adaptive dynamic regret bound for this setting, guaranteeing $\widetilde{\mathcal{O}}(\sqrt{(1+P_T)(T+\sum_t λ_t)})$ regret, where $P_T$ is the path length of the comparator sequence over $T$ rounds. This recovers the optimal guarantees for both static and dynamic regret in standard OCO as a special case where $λ_t=0$ for all rounds. To demonstrate the versatility of our results, we consider two applications: OCO with delayed feedback and OCO with time-varying memory. We show that both problems can be translated into time-varying movement costs, establishing a novel reduction specifically for the delayed feedback setting that is of independent interest. A crucial observation is that the first-order dependence on movement costs in our regret bound plays a key role in enabling optimal comparator-adaptive dynamic regret guarantees in both settings.

Exploiting Curvature in Online Convex Optimization with Delayed Feedback

In this work, we study the online convex optimization problem with curved losses and delayed feedback. When losses are strongly convex, existing approaches obtain regret bounds of order $d_{\max} \ln T$, where $d_{\max}$ is the maximum delay and $T$ is the time horizon. However, in many cases, this guarantee can be much worse than $\sqrt{d_{\mathrm{tot}}}$ as obtained by a delayed version of online gradient descent, where $d_{\mathrm{tot}}$ is the total delay. We bridge this gap by proposing a variant of follow-the-regularized-leader that obtains regret of order $\min\{\sigma_{\max}\ln T, \sqrt{d_{\mathrm{tot}}}\}$, where $\sigma_{\max}$ is the maximum number of missing observations. We then consider exp-concave losses and extend the Online Newton Step algorithm to handle delays with an adaptive learning rate tuning, achieving regret $\min\{d_{\max} n\ln T, \sqrt{d_{\mathrm{tot}}}\}$ where $n$ is the dimension. To our knowledge, this is the first algorithm to achieve such a regret bound for exp-concave losses. We further consider the problem of unconstrained online linear regression and achieve a similar guarantee by designing a variant of the Vovk-Azoury-Warmuth forecaster with a clipping trick. Finally, we implement our algorithms and conduct experiments under various types of delay and losses, showing an improved performance over existing methods.

Of Dice and Games: A Theory of Generalized Boosting

Cost-sensitive loss functions are crucial in many real-world prediction problems, where different types of errors are penalized differently; for example, in medical diagnosis, a false negative prediction can lead to worse consequences than a false positive prediction. However, traditional PAC learning theory has mostly focused on the symmetric 0-1 loss, leaving cost-sensitive losses largely unaddressed. In this work, we extend the celebrated theory of boosting to incorporate both cost-sensitive and multi-objective losses. Cost-sensitive losses assign costs to the entries of a confusion matrix, and are used to control the sum of prediction errors accounting for the cost of each error type. Multi-objective losses, on the other hand, simultaneously track multiple cost-sensitive losses, and are useful when the goal is to satisfy several criteria at once (e.g., minimizing false positives while keeping false negatives below a critical threshold). We develop a comprehensive theory of cost-sensitive and multi-objective boosting, providing a taxonomy of weak learning guarantees that distinguishes which guarantees are trivial (i.e., can always be achieved), which ones are boostable (i.e., imply strong learning), and which ones are intermediate, implying non-trivial yet not arbitrarily accurate learning. For binary classification, we establish a dichotomy: a weak learning guarantee is either trivial or boostable. In the multiclass setting, we describe a more intricate landscape of intermediate weak learning guarantees. Our characterization relies on a geometric interpretation of boosting, revealing a surprising equivalence between cost-sensitive and multi-objective losses.

Improved Regret Bounds for Bandits with Expert Advice

In this research note, we revisit the bandits with expert advice problem. Under a restricted feedback model, we prove a lower bound of order $\sqrt{K T \ln(N/K)}$ for the worst-case regret, where $K$ is the number of actions, $N>K$ the number of experts, and $T$ the time horizon. This matches a previously known upper bound of the same order and improves upon the best available lower bound of $\sqrt{K T (\ln N) / (\ln K)}$. For the standard feedback model, we prove a new instance-based upper bound that depends on the agreement between the experts and provides a logarithmic improvement compared to prior results.

A Theory of Interpretable Approximations

Can a deep neural network be approximated by a small decision tree based on simple features? This question and its variants are behind the growing demand for machine learning models that are *interpretable* by humans. In this work we study such questions by introducing *interpretable approximations*, a notion that captures the idea of approximating a target concept $c$ by a small aggregation of concepts from some base class $\mathcal{H}$. In particular, we consider the approximation of a binary concept $c$ by decision trees based on a simple class $\mathcal{H}$ (e.g., of bounded VC dimension), and use the tree depth as a measure of complexity. Our primary contribution is the following remarkable trichotomy. For any given pair of $\mathcal{H}$ and $c$, exactly one of these cases holds: (i) $c$ cannot be approximated by $\mathcal{H}$ with arbitrary accuracy; (ii) $c$ can be approximated by $\mathcal{H}$ with arbitrary accuracy, but there exists no universal rate that bounds the complexity of the approximations as a function of the accuracy; or (iii) there exists a constant $\kappa$ that depends only on $\mathcal{H}$ and $c$ such that, for *any* data distribution and *any* desired accuracy level, $c$ can be approximated by $\mathcal{H}$ with a complexity not exceeding $\kappa$. This taxonomy stands in stark contrast to the landscape of supervised classification, which offers a complex array of distribution-free and universally learnable scenarios. We show that, in the case of interpretable approximations, even a slightly nontrivial a-priori guarantee on the complexity of approximations implies approximations with constant (distribution-free and accuracy-free) complexity. We extend our trichotomy to classes $\mathcal{H}$ of unbounded VC dimension and give characterizations of interpretability based on the algebra generated by $\mathcal{H}$.

Efficient Algorithms for Learning Monophonic Halfspaces in Graphs

We study the problem of learning a binary classifier on the vertices of a graph. In particular, we consider classifiers given by monophonic halfspaces, partitions of the vertices that are convex in a certain abstract sense. Monophonic halfspaces, and related notions such as geodesic halfspaces,have recently attracted interest, and several connections have been drawn between their properties(e.g., their VC dimension) and the structure of the underlying graph $G$. We prove several novel results for learning monophonic halfspaces in the supervised, online, and active settings. Our main result is that a monophonic halfspace can be learned with near-optimal passive sample complexity in time polynomial in $n = |V(G)|$. This requires us to devise a polynomial-time algorithm for consistent hypothesis checking, based on several structural insights on monophonic halfspaces and on a reduction to $2$-satisfiability. We prove similar results for the online and active settings. We also show that the concept class can be enumerated with delay $\operatorname{poly}(n)$, and that empirical risk minimization can be performed in time $2^{\omega(G)}\operatorname{poly}(n)$ where $\omega(G)$ is the clique number of $G$. These results answer open questions from the literature (Gonz\'alez et al., 2020), and show a contrast with geodesic halfspaces, for which some of the said problems are NP-hard (Seiffarth et al., 2023).

An Improved Uniform Convergence Bound with Fat-Shattering Dimension

The fat-shattering dimension characterizes the uniform convergence property of real-valued functions. The state-of-the-art upper bounds feature a multiplicative squared logarithmic factor on the sample complexity, leaving an open gap with the existing lower bound. We provide an improved uniform convergence bound that closes this gap.

Delayed Bandits: When Do Intermediate Observations Help?

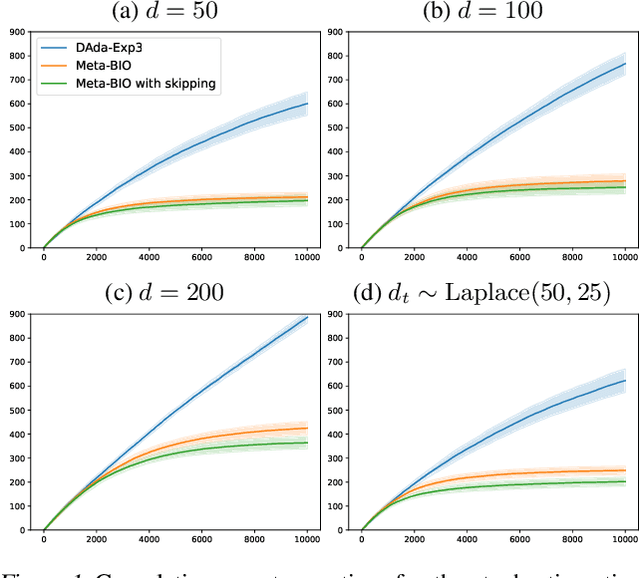
We study a $K$-armed bandit with delayed feedback and intermediate observations. We consider a model where intermediate observations have a form of a finite state, which is observed immediately after taking an action, whereas the loss is observed after an adversarially chosen delay. We show that the regime of the mapping of states to losses determines the complexity of the problem, irrespective of whether the mapping of actions to states is stochastic or adversarial. If the mapping of states to losses is adversarial, then the regret rate is of order $\sqrt{(K+d)T}$ (within log factors), where $T$ is the time horizon and $d$ is a fixed delay. This matches the regret rate of a $K$-armed bandit with delayed feedback and without intermediate observations, implying that intermediate observations are not helpful. However, if the mapping of states to losses is stochastic, we show that the regret grows at a rate of $\sqrt{\big(K+\min\{|\mathcal{S}|,d\}\big)T}$ (within log factors), implying that if the number $|\mathcal{S}|$ of states is smaller than the delay, then intermediate observations help. We also provide refined high-probability regret upper bounds for non-uniform delays, together with experimental validation of our algorithms.

On the Minimax Regret for Online Learning with Feedback Graphs

In this work, we improve on the upper and lower bounds for the regret of online learning with strongly observable undirected feedback graphs. The best known upper bound for this problem is $\mathcal{O}\bigl(\sqrt{\alpha T\ln K}\bigr)$, where $K$ is the number of actions, $\alpha$ is the independence number of the graph, and $T$ is the time horizon. The $\sqrt{\ln K}$ factor is known to be necessary when $\alpha = 1$ (the experts case). On the other hand, when $\alpha = K$ (the bandits case), the minimax rate is known to be $\Theta\bigl(\sqrt{KT}\bigr)$, and a lower bound $\Omega\bigl(\sqrt{\alpha T}\bigr)$ is known to hold for any $\alpha$. Our improved upper bound $\mathcal{O}\bigl(\sqrt{\alpha T(1+\ln(K/\alpha))}\bigr)$ holds for any $\alpha$ and matches the lower bounds for bandits and experts, while interpolating intermediate cases. To prove this result, we use FTRL with $q$-Tsallis entropy for a carefully chosen value of $q \in [1/2, 1)$ that varies with $\alpha$. The analysis of this algorithm requires a new bound on the variance term in the regret. We also show how to extend our techniques to time-varying graphs, without requiring prior knowledge of their independence numbers. Our upper bound is complemented by an improved $\Omega\bigl(\sqrt{\alpha T(\ln K)/(\ln\alpha)}\bigr)$ lower bound for all $\alpha > 1$, whose analysis relies on a novel reduction to multitask learning. This shows that a logarithmic factor is necessary as soon as $\alpha < K$.