Online Newton Method for Bandit Convex Optimisation

We introduce a computationally efficient algorithm for zeroth-order bandit convex optimisation and prove that in the adversarial setting its regret is at most $d^{3.5} \sqrt{n} \mathrm{polylog}(n, d)$ with high probability where $d$ is the dimension and $n$ is the time horizon. In the stochastic setting the bound improves to $M d^{2} \sqrt{n} \mathrm{polylog}(n, d)$ where $M \in [d^{-1/2}, d^{-1 / 4}]$ is a constant that depends on the geometry of the constraint set and the desired computational properties.

High-Probability Risk Bounds via Sequential Predictors

Online learning methods yield sequential regret bounds under minimal assumptions and provide in-expectation risk bounds for statistical learning. However, despite the apparent advantage of online guarantees over their statistical counterparts, recent findings indicate that in many important cases, regret bounds may not guarantee tight high-probability risk bounds in the statistical setting. In this work we show that online to batch conversions applied to general online learning algorithms can bypass this limitation. Via a general second-order correction to the loss function defining the regret, we obtain nearly optimal high-probability risk bounds for several classical statistical estimation problems, such as discrete distribution estimation, linear regression, logistic regression, and conditional density estimation. Our analysis relies on the fact that many online learning algorithms are improper, as they are not restricted to use predictors from a given reference class. The improper nature of our estimators enables significant improvements in the dependencies on various problem parameters. Finally, we discuss some computational advantages of our sequential algorithms over their existing batch counterparts.

Trading-Off Payments and Accuracy in Online Classification with Paid Stochastic Experts

We investigate online classification with paid stochastic experts. Here, before making their prediction, each expert must be paid. The amount that we pay each expert directly influences the accuracy of their prediction through some unknown Lipschitz "productivity" function. In each round, the learner must decide how much to pay each expert and then make a prediction. They incur a cost equal to a weighted sum of the prediction error and upfront payments for all experts. We introduce an online learning algorithm whose total cost after $T$ rounds exceeds that of a predictor which knows the productivity of all experts in advance by at most $\mathcal{O}(K^2(\log T)\sqrt{T})$ where $K$ is the number of experts. In order to achieve this result, we combine Lipschitz bandits and online classification with surrogate losses. These tools allow us to improve upon the bound of order $T^{2/3}$ one would obtain in the standard Lipschitz bandit setting. Our algorithm is empirically evaluated on synthetic data

Delayed Bandits: When Do Intermediate Observations Help?

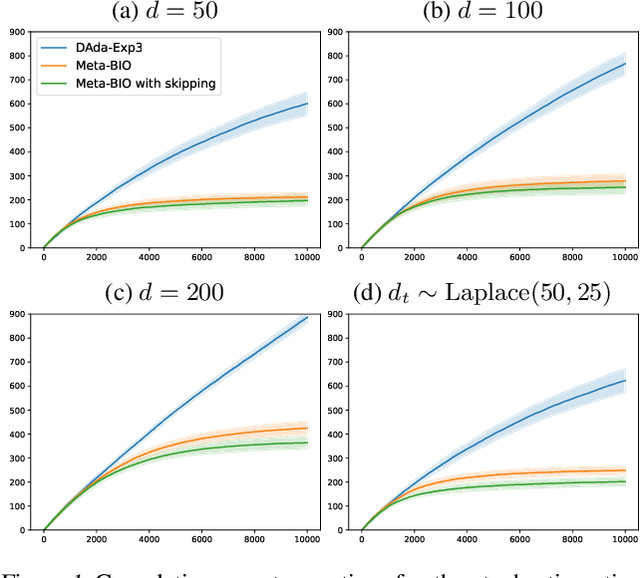
We study a $K$-armed bandit with delayed feedback and intermediate observations. We consider a model where intermediate observations have a form of a finite state, which is observed immediately after taking an action, whereas the loss is observed after an adversarially chosen delay. We show that the regime of the mapping of states to losses determines the complexity of the problem, irrespective of whether the mapping of actions to states is stochastic or adversarial. If the mapping of states to losses is adversarial, then the regret rate is of order $\sqrt{(K+d)T}$ (within log factors), where $T$ is the time horizon and $d$ is a fixed delay. This matches the regret rate of a $K$-armed bandit with delayed feedback and without intermediate observations, implying that intermediate observations are not helpful. However, if the mapping of states to losses is stochastic, we show that the regret grows at a rate of $\sqrt{\big(K+\min\{|\mathcal{S}|,d\}\big)T}$ (within log factors), implying that if the number $|\mathcal{S}|$ of states is smaller than the delay, then intermediate observations help. We also provide refined high-probability regret upper bounds for non-uniform delays, together with experimental validation of our algorithms.

A Unified Analysis of Nonstochastic Delayed Feedback for Combinatorial Semi-Bandits, Linear Bandits, and MDPs

We derive a new analysis of Follow The Regularized Leader (FTRL) for online learning with delayed bandit feedback. By separating the cost of delayed feedback from that of bandit feedback, our analysis allows us to obtain new results in three important settings. On the one hand, we derive the first optimal (up to logarithmic factors) regret bounds for combinatorial semi-bandits with delay and adversarial Markov decision processes with delay (and known transition functions). On the other hand, we use our analysis to derive an efficient algorithm for linear bandits with delay achieving near-optimal regret bounds. Our novel regret decomposition shows that FTRL remains stable across multiple rounds under mild assumptions on the Hessian of the regularizer.

Learning on the Edge: Online Learning with Stochastic Feedback Graphs

The framework of feedback graphs is a generalization of sequential decision-making with bandit or full information feedback. In this work, we study an extension where the directed feedback graph is stochastic, following a distribution similar to the classical Erd\H{o}s-R\'enyi model. Specifically, in each round every edge in the graph is either realized or not with a distinct probability for each edge. We prove nearly optimal regret bounds of order $\min\bigl\{\min_{\varepsilon} \sqrt{(\alpha_\varepsilon/\varepsilon) T},\, \min_{\varepsilon} (\delta_\varepsilon/\varepsilon)^{1/3} T^{2/3}\bigr\}$ (ignoring logarithmic factors), where $\alpha_{\varepsilon}$ and $\delta_{\varepsilon}$ are graph-theoretic quantities measured on the support of the stochastic feedback graph $\mathcal{G}$ with edge probabilities thresholded at $\varepsilon$. Our result, which holds without any preliminary knowledge about $\mathcal{G}$, requires the learner to observe only the realized out-neighborhood of the chosen action. When the learner is allowed to observe the realization of the entire graph (but only the losses in the out-neighborhood of the chosen action), we derive a more efficient algorithm featuring a dependence on weighted versions of the independence and weak domination numbers that exhibits improved bounds for some special cases.

A Regret-Variance Trade-Off in Online Learning

We consider prediction with expert advice for strongly convex and bounded losses, and investigate trade-offs between regret and "variance" (i.e., squared difference of learner's predictions and best expert predictions). With $K$ experts, the Exponentially Weighted Average (EWA) algorithm is known to achieve $O(\log K)$ regret. We prove that a variant of EWA either achieves a negative regret (i.e., the algorithm outperforms the best expert), or guarantees a $O(\log K)$ bound on both variance and regret. Building on this result, we show several examples of how variance of predictions can be exploited in learning. In the online to batch analysis, we show that a large empirical variance allows to stop the online to batch conversion early and outperform the risk of the best predictor in the class. We also recover the optimal rate of model selection aggregation when we do not consider early stopping. In online prediction with corrupted losses, we show that the effect of corruption on the regret can be compensated by a large variance. In online selective sampling, we design an algorithm that samples less when the variance is large, while guaranteeing the optimal regret bound in expectation. In online learning with abstention, we use a similar term as the variance to derive the first high-probability $O(\log K)$ regret bound in this setting. Finally, we extend our results to the setting of online linear regression.

A Near-Optimal Best-of-Both-Worlds Algorithm for Online Learning with Feedback Graphs

We consider online learning with feedback graphs, a sequential decision-making framework where the learner's feedback is determined by a directed graph over the action set. We present a computationally efficient algorithm for learning in this framework that simultaneously achieves near-optimal regret bounds in both stochastic and adversarial environments. The bound against oblivious adversaries is $\tilde{O} (\sqrt{\alpha T})$, where $T$ is the time horizon and $\alpha$ is the independence number of the feedback graph. The bound against stochastic environments is $O\big( (\ln T)^2 \max_{S\in \mathcal I(G)} \sum_{i \in S} \Delta_i^{-1}\big)$ where $\mathcal I(G)$ is the family of all independent sets in a suitably defined undirected version of the graph and $\Delta_i$ are the suboptimality gaps. The algorithm combines ideas from the EXP3++ algorithm for stochastic and adversarial bandits and the EXP3.G algorithm for feedback graphs with a novel exploration scheme. The scheme, which exploits the structure of the graph to reduce exploration, is key to obtain best-of-both-worlds guarantees with feedback graphs. We also extend our algorithm and results to a setting where the feedback graphs are allowed to change over time.

Nonstochastic Bandits and Experts with Arm-Dependent Delays

We study nonstochastic bandits and experts in a delayed setting where delays depend on both time and arms. While the setting in which delays only depend on time has been extensively studied, the arm-dependent delay setting better captures real-world applications at the cost of introducing new technical challenges. In the full information (experts) setting, we design an algorithm with a first-order regret bound that reveals an interesting trade-off between delays and losses. We prove a similar first-order regret bound also for the bandit setting, when the learner is allowed to observe how many losses are missing. These are the first bounds in the delayed setting that depend on the losses and delays of the best arm only. When in the bandit setting no information other than the losses is observed, we still manage to prove a regret bound through a modification to the algorithm of Zimmert and Seldin (2020). Our analyses hinge on a novel bound on the drift, measuring how much better an algorithm can perform when given a look-ahead of one round.

Beyond Bandit Feedback in Online Multiclass Classification

We study the problem of online multiclass classification in a setting where the learner's feedback is determined by an arbitrary directed graph. While including bandit feedback as a special case, feedback graphs allow a much richer set of applications, including filtering and label efficient classification. We introduce Gappletron, the first online multiclass algorithm that works with arbitrary feedback graphs. For this new algorithm, we prove surrogate regret bounds that hold, both in expectation and with high probability, for a large class of surrogate losses. Our bounds are of order $B\sqrt{\rho KT}$, where $B$ is the diameter of the prediction space, $K$ is the number of classes, $T$ is the time horizon, and $\rho$ is the domination number (a graph-theoretic parameter affecting the amount of exploration). In the full information case, we show that Gappletron achieves a constant surrogate regret of order $B^2K$. We also prove a general lower bound of order $\max\big\{B^2K,\sqrt{T}\big\}$ showing that our upper bounds are not significantly improvable. Experiments on synthetic data show that for various feedback graphs, our algorithm is competitive against known baselines.