Sample-efficient Learning of Concepts with Theoretical Guarantees: from Data to Concepts without Interventions

Machine learning is a vital part of many real-world systems, but several concerns remain about the lack of interpretability, explainability and robustness of black-box AI systems. Concept-based models (CBM) address some of these challenges by learning interpretable concepts from high-dimensional data, e.g. images, which are used to predict labels. An important issue in CBMs is concept leakage, i.e., spurious information in the learned concepts, which effectively leads to learning "wrong" concepts. Current mitigating strategies are heuristic, have strong assumptions, e.g., they assume that the concepts are statistically independent of each other, or require substantial human interaction in terms of both interventions and labels provided by annotators. In this paper, we describe a framework that provides theoretical guarantees on the correctness of the learned concepts and on the number of required labels, without requiring any interventions. Our framework leverages causal representation learning (CRL) to learn high-level causal variables from low-level data, and learns to align these variables with interpretable concepts. We propose a linear and a non-parametric estimator for this mapping, providing a finite-sample high probability result in the linear case and an asymptotic consistency result for the non-parametric estimator. We implement our framework with state-of-the-art CRL methods, and show its efficacy in learning the correct concepts in synthetic and image benchmarks.

Online Newton Method for Bandit Convex Optimisation

We introduce a computationally efficient algorithm for zeroth-order bandit convex optimisation and prove that in the adversarial setting its regret is at most $d^{3.5} \sqrt{n} \mathrm{polylog}(n, d)$ with high probability where $d$ is the dimension and $n$ is the time horizon. In the stochastic setting the bound improves to $M d^{2} \sqrt{n} \mathrm{polylog}(n, d)$ where $M \in [d^{-1/2}, d^{-1 / 4}]$ is a constant that depends on the geometry of the constraint set and the desired computational properties.

The Risks of Recourse in Binary Classification

Algorithmic recourse provides explanations that help users overturn an unfavorable decision by a machine learning system. But so far very little attention has been paid to whether providing recourse is beneficial or not. We introduce an abstract learning-theoretic framework that compares the risks (i.e. expected losses) for classification with and without algorithmic recourse. This allows us to answer the question of when providing recourse is beneficial or harmful at the population level. Surprisingly, we find that there are many plausible scenarios in which providing recourse turns out to be harmful, because it pushes users to regions of higher class uncertainty and therefore leads to more mistakes. We further study whether the party deploying the classifier has an incentive to strategize in anticipation of having to provide recourse, and we find that sometimes they do, to the detriment of their users. Providing algorithmic recourse may therefore also be harmful at the systemic level. We confirm our theoretical findings in experiments on simulated and real-world data. All in all, we conclude that the current concept of algorithmic recourse is not reliably beneficial, and therefore requires rethinking.

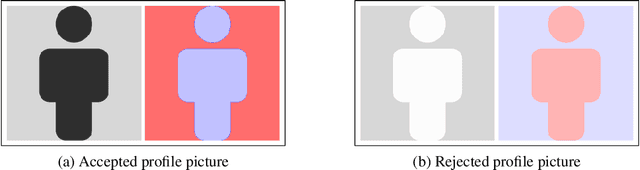
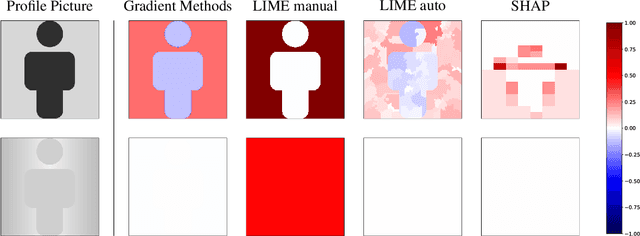
Attribution-based Explanations that Provide Recourse Cannot be Robust

Different users of machine learning methods require different explanations, depending on their goals. To make machine learning accountable to society, one important goal is to get actionable options for recourse, which allow an affected user to change the decision $f(x)$ of a machine learning system by making limited changes to its input $x$. We formalize this by providing a general definition of recourse sensitivity, which needs to be instantiated with a utility function that describes which changes to the decisions are relevant to the user. This definition applies to local attribution methods, which attribute an importance weight to each input feature. It is often argued that such local attributions should be robust, in the sense that a small change in the input $x$ that is being explained, should not cause a large change in the feature weights. However, we prove formally that it is in general impossible for any single attribution method to be both recourse sensitive and robust at the same time. It follows that there must always exist counterexamples to at least one of these properties. We provide such counterexamples for several popular attribution methods, including LIME, SHAP, Integrated Gradients and SmoothGrad. Our results also cover counterfactual explanations, which may be viewed as attributions that describe a perturbation of $x$. We further discuss possible ways to work around our impossibility result, for instance by allowing the output to consist of sets with multiple attributions. Finally, we strengthen our impossibility result for the restricted case where users are only able to change a single attribute of x, by providing an exact characterization of the functions $f$ to which impossibility applies.