Combining Causal Models for More Accurate Abstractions of Neural Networks

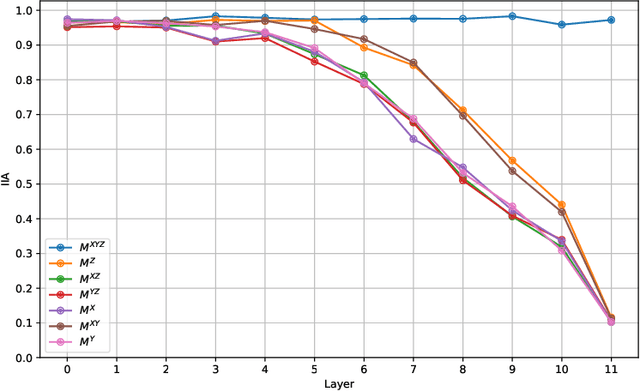
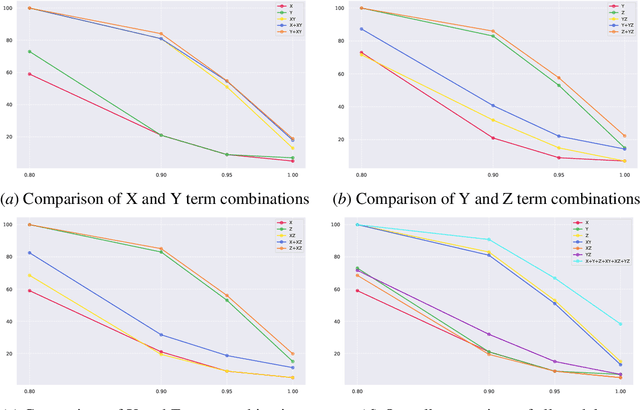
Mechanistic interpretability aims to reverse engineer neural networks by uncovering which high-level algorithms they implement. Causal abstraction provides a precise notion of when a network implements an algorithm, i.e., a causal model of the network contains low-level features that realize the high-level variables in a causal model of the algorithm. A typical problem in practical settings is that the algorithm is not an entirely faithful abstraction of the network, meaning it only partially captures the true reasoning process of a model. We propose a solution where we combine different simple high-level models to produce a more faithful representation of the network. Through learning this combination, we can model neural networks as being in different computational states depending on the input provided, which we show is more accurate to GPT 2-small fine-tuned on two toy tasks. We observe a trade-off between the strength of an interpretability hypothesis, which we define in terms of the number of inputs explained by the high-level models, and its faithfulness, which we define as the interchange intervention accuracy. Our method allows us to modulate between the two, providing the most accurate combination of models that describe the behavior of a neural network given a faithfulness level.

Learning to Defer for Causal Discovery with Imperfect Experts

Integrating expert knowledge, e.g. from large language models, into causal discovery algorithms can be challenging when the knowledge is not guaranteed to be correct. Expert recommendations may contradict data-driven results, and their reliability can vary significantly depending on the domain or specific query. Existing methods based on soft constraints or inconsistencies in predicted causal relationships fail to account for these variations in expertise. To remedy this, we propose L2D-CD, a method for gauging the correctness of expert recommendations and optimally combining them with data-driven causal discovery results. By adapting learning-to-defer (L2D) algorithms for pairwise causal discovery (CD), we learn a deferral function that selects whether to rely on classical causal discovery methods using numerical data or expert recommendations based on textual meta-data. We evaluate L2D-CD on the canonical T\"ubingen pairs dataset and demonstrate its superior performance compared to both the causal discovery method and the expert used in isolation. Moreover, our approach identifies domains where the expert's performance is strong or weak. Finally, we outline a strategy for generalizing this approach to causal discovery on graphs with more than two variables, paving the way for further research in this area.

SNAP: Sequential Non-Ancestor Pruning for Targeted Causal Effect Estimation With an Unknown Graph

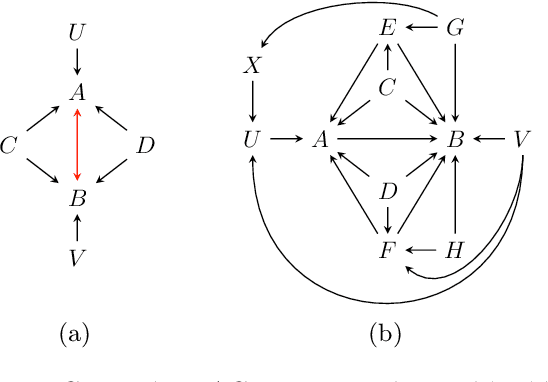
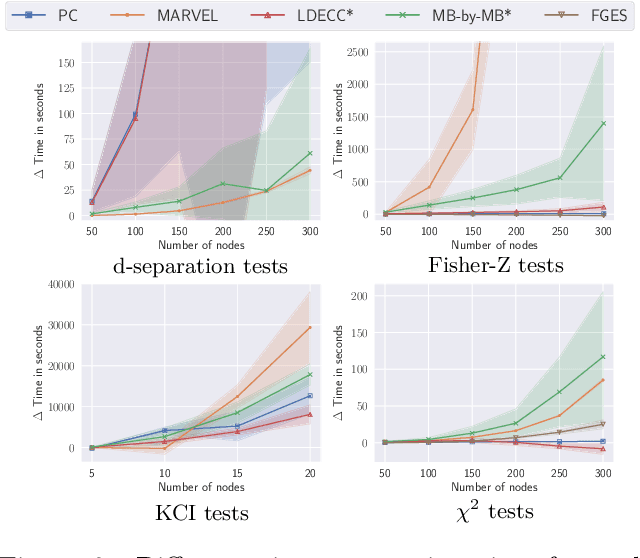
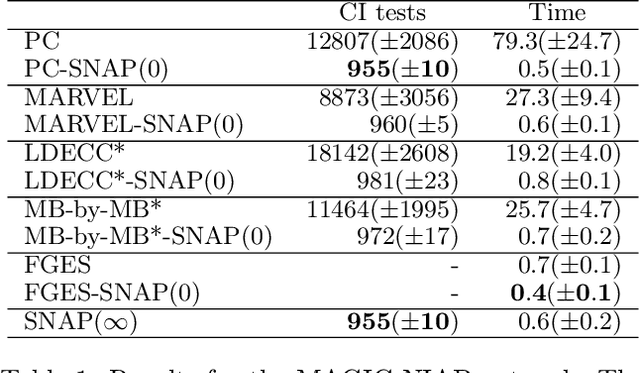
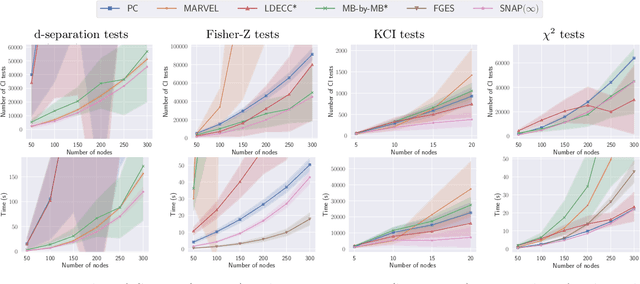
Causal discovery can be computationally demanding for large numbers of variables. If we only wish to estimate the causal effects on a small subset of target variables, we might not need to learn the causal graph for all variables, but only a small subgraph that includes the targets and their adjustment sets. In this paper, we focus on identifying causal effects between target variables in a computationally and statistically efficient way. This task combines causal discovery and effect estimation, aligning the discovery objective with the effects to be estimated. We show that definite non-ancestors of the targets are unnecessary to learn causal relations between the targets and to identify efficient adjustments sets. We sequentially identify and prune these definite non-ancestors with our Sequential Non-Ancestor Pruning (SNAP) framework, which can be used either as a preprocessing step to standard causal discovery methods, or as a standalone sound and complete causal discovery algorithm. Our results on synthetic and real data show that both approaches substantially reduce the number of independence tests and the computation time without compromising the quality of causal effect estimations.

Sample-efficient Learning of Concepts with Theoretical Guarantees: from Data to Concepts without Interventions

Machine learning is a vital part of many real-world systems, but several concerns remain about the lack of interpretability, explainability and robustness of black-box AI systems. Concept-based models (CBM) address some of these challenges by learning interpretable concepts from high-dimensional data, e.g. images, which are used to predict labels. An important issue in CBMs is concept leakage, i.e., spurious information in the learned concepts, which effectively leads to learning "wrong" concepts. Current mitigating strategies are heuristic, have strong assumptions, e.g., they assume that the concepts are statistically independent of each other, or require substantial human interaction in terms of both interventions and labels provided by annotators. In this paper, we describe a framework that provides theoretical guarantees on the correctness of the learned concepts and on the number of required labels, without requiring any interventions. Our framework leverages causal representation learning (CRL) to learn high-level causal variables from low-level data, and learns to align these variables with interpretable concepts. We propose a linear and a non-parametric estimator for this mapping, providing a finite-sample high probability result in the linear case and an asymptotic consistency result for the non-parametric estimator. We implement our framework with state-of-the-art CRL methods, and show its efficacy in learning the correct concepts in synthetic and image benchmarks.

Amortized Equation Discovery in Hybrid Dynamical Systems

Hybrid dynamical systems are prevalent in science and engineering to express complex systems with continuous and discrete states. To learn the laws of systems, all previous methods for equation discovery in hybrid systems follow a two-stage paradigm, i.e. they first group time series into small cluster fragments and then discover equations in each fragment separately through methods in non-hybrid systems. Although effective, these methods do not fully take advantage of the commonalities in the shared dynamics of multiple fragments that are driven by the same equations. Besides, the two-stage paradigm breaks the interdependence between categorizing and representing dynamics that jointly form hybrid systems. In this paper, we reformulate the problem and propose an end-to-end learning framework, i.e. Amortized Equation Discovery (AMORE), to jointly categorize modes and discover equations characterizing the dynamics of each mode by all segments of the mode. Experiments on four hybrid and six non-hybrid systems show that our method outperforms previous methods on equation discovery, segmentation, and forecasting.

Learning Causal Abstractions of Linear Structural Causal Models

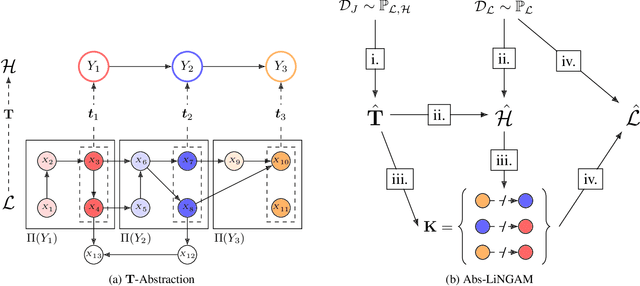
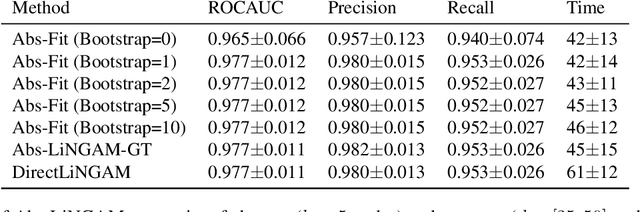
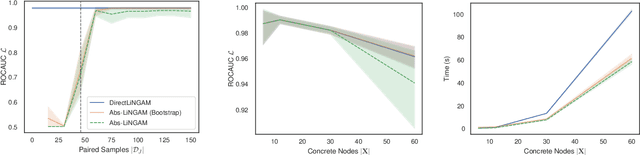
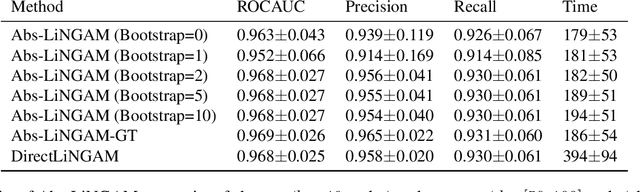
The need for modelling causal knowledge at different levels of granularity arises in several settings. Causal Abstraction provides a framework for formalizing this problem by relating two Structural Causal Models at different levels of detail. Despite increasing interest in applying causal abstraction, e.g. in the interpretability of large machine learning models, the graphical and parametrical conditions under which a causal model can abstract another are not known. Furthermore, learning causal abstractions from data is still an open problem. In this work, we tackle both issues for linear causal models with linear abstraction functions. First, we characterize how the low-level coefficients and the abstraction function determine the high-level coefficients and how the high-level model constrains the causal ordering of low-level variables. Then, we apply our theoretical results to learn high-level and low-level causal models and their abstraction function from observational data. In particular, we introduce Abs-LiNGAM, a method that leverages the constraints induced by the learned high-level model and the abstraction function to speedup the recovery of the larger low-level model, under the assumption of non-Gaussian noise terms. In simulated settings, we show the effectiveness of learning causal abstractions from data and the potential of our method in improving scalability of causal discovery.

Towards the Reusability and Compositionality of Causal Representations

Causal Representation Learning (CRL) aims at identifying high-level causal factors and their relationships from high-dimensional observations, e.g., images. While most CRL works focus on learning causal representations in a single environment, in this work we instead propose a first step towards learning causal representations from temporal sequences of images that can be adapted in a new environment, or composed across multiple related environments. In particular, we introduce DECAF, a framework that detects which causal factors can be reused and which need to be adapted from previously learned causal representations. Our approach is based on the availability of intervention targets, that indicate which variables are perturbed at each time step. Experiments on three benchmark datasets show that integrating our framework with four state-of-the-art CRL approaches leads to accurate representations in a new environment with only a few samples.

A Sparsity Principle for Partially Observable Causal Representation Learning

Causal representation learning aims at identifying high-level causal variables from perceptual data. Most methods assume that all latent causal variables are captured in the high-dimensional observations. We instead consider a partially observed setting, in which each measurement only provides information about a subset of the underlying causal state. Prior work has studied this setting with multiple domains or views, each depending on a fixed subset of latents. Here, we focus on learning from unpaired observations from a dataset with an instance-dependent partial observability pattern. Our main contribution is to establish two identifiability results for this setting: one for linear mixing functions without parametric assumptions on the underlying causal model, and one for piecewise linear mixing functions with Gaussian latent causal variables. Based on these insights, we propose two methods for estimating the underlying causal variables by enforcing sparsity in the inferred representation. Experiments on different simulated datasets and established benchmarks highlight the effectiveness of our approach in recovering the ground-truth latents.

Multi-View Causal Representation Learning with Partial Observability

We present a unified framework for studying the identifiability of representations learned from simultaneously observed views, such as different data modalities. We allow a partially observed setting in which each view constitutes a nonlinear mixture of a subset of underlying latent variables, which can be causally related. We prove that the information shared across all subsets of any number of views can be learned up to a smooth bijection using contrastive learning and a single encoder per view. We also provide graphical criteria indicating which latent variables can be identified through a simple set of rules, which we refer to as identifiability algebra. Our general framework and theoretical results unify and extend several previous works on multi-view nonlinear ICA, disentanglement, and causal representation learning. We experimentally validate our claims on numerical, image, and multi-modal data sets. Further, we demonstrate that the performance of prior methods is recovered in different special cases of our setup. Overall, we find that access to multiple partial views enables us to identify a more fine-grained representation, under the generally milder assumption of partial observability.

Learning Dynamic Attribute-factored World Models for Efficient Multi-object Reinforcement Learning

In many reinforcement learning tasks, the agent has to learn to interact with many objects of different types and generalize to unseen combinations and numbers of objects. Often a task is a composition of previously learned tasks (e.g. block stacking). These are examples of compositional generalization, in which we compose object-centric representations to solve complex tasks. Recent works have shown the benefits of object-factored representations and hierarchical abstractions for improving sample efficiency in these settings. On the other hand, these methods do not fully exploit the benefits of factorization in terms of object attributes. In this paper, we address this opportunity and introduce the Dynamic Attribute FacTored RL (DAFT-RL) framework. In DAFT-RL, we leverage object-centric representation learning to extract objects from visual inputs. We learn to classify them in classes and infer their latent parameters. For each class of object, we learn a class template graph that describes how the dynamics and reward of an object of this class factorize according to its attributes. We also learn an interaction pattern graph that describes how objects of different classes interact with each other at the attribute level. Through these graphs and a dynamic interaction graph that models the interactions between objects, we can learn a policy that can then be directly applied in a new environment by just estimating the interactions and latent parameters. We evaluate DAFT-RL in three benchmark datasets and show our framework outperforms the state-of-the-art in generalizing across unseen objects with varying attributes and latent parameters, as well as in the composition of previously learned tasks.