Interaction Asymmetry: A General Principle for Learning Composable Abstractions

Learning disentangled representations of concepts and re-composing them in unseen ways is crucial for generalizing to out-of-domain situations. However, the underlying properties of concepts that enable such disentanglement and compositional generalization remain poorly understood. In this work, we propose the principle of interaction asymmetry which states: "Parts of the same concept have more complex interactions than parts of different concepts". We formalize this via block diagonality conditions on the $(n+1)$th order derivatives of the generator mapping concepts to observed data, where different orders of "complexity" correspond to different $n$. Using this formalism, we prove that interaction asymmetry enables both disentanglement and compositional generalization. Our results unify recent theoretical results for learning concepts of objects, which we show are recovered as special cases with $n\!=\!0$ or $1$. We provide results for up to $n\!=\!2$, thus extending these prior works to more flexible generator functions, and conjecture that the same proof strategies generalize to larger $n$. Practically, our theory suggests that, to disentangle concepts, an autoencoder should penalize its latent capacity and the interactions between concepts during decoding. We propose an implementation of these criteria using a flexible Transformer-based VAE, with a novel regularizer on the attention weights of the decoder. On synthetic image datasets consisting of objects, we provide evidence that this model can achieve comparable object disentanglement to existing models that use more explicit object-centric priors.

All or None: Identifiable Linear Properties of Next-token Predictors in Language Modeling

We analyze identifiability as a possible explanation for the ubiquity of linear properties across language models, such as the vector difference between the representations of "easy" and "easiest" being parallel to that between "lucky" and "luckiest". For this, we ask whether finding a linear property in one model implies that any model that induces the same distribution has that property, too. To answer that, we first prove an identifiability result to characterize distribution-equivalent next-token predictors, lifting a diversity requirement of previous results. Second, based on a refinement of relational linearity [Paccanaro and Hinton, 2001; Hernandez et al., 2024], we show how many notions of linearity are amenable to our analysis. Finally, we show that under suitable conditions, these linear properties either hold in all or none distribution-equivalent next-token predictors.

Causal Representation Learning in Temporal Data via Single-Parent Decoding

Scientific research often seeks to understand the causal structure underlying high-level variables in a system. For example, climate scientists study how phenomena, such as El Ni\~no, affect other climate processes at remote locations across the globe. However, scientists typically collect low-level measurements, such as geographically distributed temperature readings. From these, one needs to learn both a mapping to causally-relevant latent variables, such as a high-level representation of the El Ni\~no phenomenon and other processes, as well as the causal model over them. The challenge is that this task, called causal representation learning, is highly underdetermined from observational data alone, requiring other constraints during learning to resolve the indeterminacies. In this work, we consider a temporal model with a sparsity assumption, namely single-parent decoding: each observed low-level variable is only affected by a single latent variable. Such an assumption is reasonable in many scientific applications that require finding groups of low-level variables, such as extracting regions from geographically gridded measurement data in climate research or capturing brain regions from neural activity data. We demonstrate the identifiability of the resulting model and propose a differentiable method, Causal Discovery with Single-parent Decoding (CDSD), that simultaneously learns the underlying latents and a causal graph over them. We assess the validity of our theoretical results using simulated data and showcase the practical validity of our method in an application to real-world data from the climate science field.

Sparsity regularization via tree-structured environments for disentangled representations

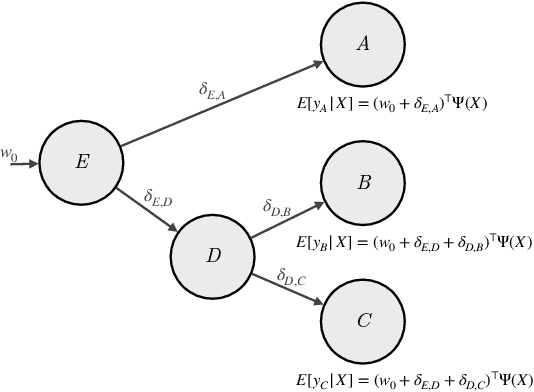
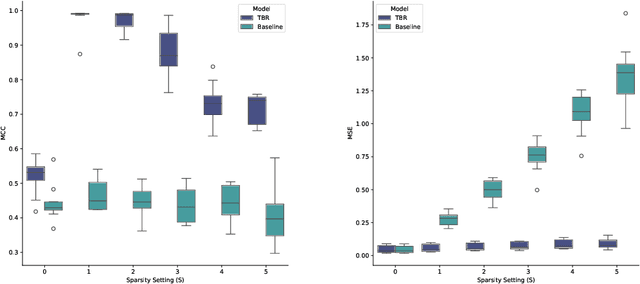
Many causal systems such as biological processes in cells can only be observed indirectly via measurements, such as gene expression. Causal representation learning -- the task of correctly mapping low-level observations to latent causal variables -- could advance scientific understanding by enabling inference of latent variables such as pathway activation. In this paper, we develop methods for inferring latent variables from multiple related datasets (environments) and tasks. As a running example, we consider the task of predicting a phenotype from gene expression, where we often collect data from multiple cell types or organisms that are related in known ways. The key insight is that the mapping from latent variables driven by gene expression to the phenotype of interest changes sparsely across closely related environments. To model sparse changes, we introduce Tree-Based Regularization (TBR), an objective that minimizes both prediction error and regularizes closely related environments to learn similar predictors. We prove that under assumptions about the degree of sparse changes, TBR identifies the true latent variables up to some simple transformations. We evaluate the theory empirically with both simulations and ground-truth gene expression data. We find that TBR recovers the latent causal variables better than related methods across these settings, even under settings that violate some assumptions of the theory.

Leveraging Structure Between Environments: Phylogenetic Regularization Incentivizes Disentangled Representations

Many causal systems such as biological processes in cells can only be observed indirectly via measurements, such as gene expression. Causal representation learning -- the task of correctly mapping low-level observations to latent causal variables -- could advance scientific understanding by enabling inference of latent variables such as pathway activation. In this paper, we develop methods for inferring latent variables from multiple related datasets (environments) and tasks. As a running example, we consider the task of predicting a phenotype from gene expression, where we often collect data from multiple cell types or organisms that are related in known ways. The key insight is that the mapping from latent variables driven by gene expression to the phenotype of interest changes sparsely across closely related environments. To model sparse changes, we introduce Tree-Based Regularization (TBR), an objective that minimizes both prediction error and regularizes closely related environments to learn similar predictors. We prove that under assumptions about the degree of sparse changes, TBR identifies the true latent variables up to some simple transformations. We evaluate the theory empirically with both simulations and ground-truth gene expression data. We find that TBR recovers the latent causal variables better than related methods across these settings, even under settings that violate some assumptions of the theory.

A Sparsity Principle for Partially Observable Causal Representation Learning

Causal representation learning aims at identifying high-level causal variables from perceptual data. Most methods assume that all latent causal variables are captured in the high-dimensional observations. We instead consider a partially observed setting, in which each measurement only provides information about a subset of the underlying causal state. Prior work has studied this setting with multiple domains or views, each depending on a fixed subset of latents. Here, we focus on learning from unpaired observations from a dataset with an instance-dependent partial observability pattern. Our main contribution is to establish two identifiability results for this setting: one for linear mixing functions without parametric assumptions on the underlying causal model, and one for piecewise linear mixing functions with Gaussian latent causal variables. Based on these insights, we propose two methods for estimating the underlying causal variables by enforcing sparsity in the inferred representation. Experiments on different simulated datasets and established benchmarks highlight the effectiveness of our approach in recovering the ground-truth latents.

Nonparametric Partial Disentanglement via Mechanism Sparsity: Sparse Actions, Interventions and Sparse Temporal Dependencies

This work introduces a novel principle for disentanglement we call mechanism sparsity regularization, which applies when the latent factors of interest depend sparsely on observed auxiliary variables and/or past latent factors. We propose a representation learning method that induces disentanglement by simultaneously learning the latent factors and the sparse causal graphical model that explains them. We develop a nonparametric identifiability theory that formalizes this principle and shows that the latent factors can be recovered by regularizing the learned causal graph to be sparse. More precisely, we show identifiablity up to a novel equivalence relation we call "consistency", which allows some latent factors to remain entangled (hence the term partial disentanglement). To describe the structure of this entanglement, we introduce the notions of entanglement graphs and graph preserving functions. We further provide a graphical criterion which guarantees complete disentanglement, that is identifiability up to permutations and element-wise transformations. We demonstrate the scope of the mechanism sparsity principle as well as the assumptions it relies on with several worked out examples. For instance, the framework shows how one can leverage multi-node interventions with unknown targets on the latent factors to disentangle them. We further draw connections between our nonparametric results and the now popular exponential family assumption. Lastly, we propose an estimation procedure based on variational autoencoders and a sparsity constraint and demonstrate it on various synthetic datasets. This work is meant to be a significantly extended version of Lachapelle et al. (2022).

Multi-View Causal Representation Learning with Partial Observability

We present a unified framework for studying the identifiability of representations learned from simultaneously observed views, such as different data modalities. We allow a partially observed setting in which each view constitutes a nonlinear mixture of a subset of underlying latent variables, which can be causally related. We prove that the information shared across all subsets of any number of views can be learned up to a smooth bijection using contrastive learning and a single encoder per view. We also provide graphical criteria indicating which latent variables can be identified through a simple set of rules, which we refer to as identifiability algebra. Our general framework and theoretical results unify and extend several previous works on multi-view nonlinear ICA, disentanglement, and causal representation learning. We experimentally validate our claims on numerical, image, and multi-modal data sets. Further, we demonstrate that the performance of prior methods is recovered in different special cases of our setup. Overall, we find that access to multiple partial views enables us to identify a more fine-grained representation, under the generally milder assumption of partial observability.

Additive Decoders for Latent Variables Identification and Cartesian-Product Extrapolation

We tackle the problems of latent variables identification and "out-of-support" image generation in representation learning. We show that both are possible for a class of decoders that we call additive, which are reminiscent of decoders used for object-centric representation learning (OCRL) and well suited for images that can be decomposed as a sum of object-specific images. We provide conditions under which exactly solving the reconstruction problem using an additive decoder is guaranteed to identify the blocks of latent variables up to permutation and block-wise invertible transformations. This guarantee relies only on very weak assumptions about the distribution of the latent factors, which might present statistical dependencies and have an almost arbitrarily shaped support. Our result provides a new setting where nonlinear independent component analysis (ICA) is possible and adds to our theoretical understanding of OCRL methods. We also show theoretically that additive decoders can generate novel images by recombining observed factors of variations in novel ways, an ability we refer to as Cartesian-product extrapolation. We show empirically that additivity is crucial for both identifiability and extrapolation on simulated data.

Synergies Between Disentanglement and Sparsity: a Multi-Task Learning Perspective

Although disentangled representations are often said to be beneficial for downstream tasks, current empirical and theoretical understanding is limited. In this work, we provide evidence that disentangled representations coupled with sparse base-predictors improve generalization. In the context of multi-task learning, we prove a new identifiability result that provides conditions under which maximally sparse base-predictors yield disentangled representations. Motivated by this theoretical result, we propose a practical approach to learn disentangled representations based on a sparsity-promoting bi-level optimization problem. Finally, we explore a meta-learning version of this algorithm based on group Lasso multiclass SVM base-predictors, for which we derive a tractable dual formulation. It obtains competitive results on standard few-shot classification benchmarks, while each task is using only a fraction of the learned representations.