Nonparametric Partial Disentanglement via Mechanism Sparsity: Sparse Actions, Interventions and Sparse Temporal Dependencies

This work introduces a novel principle for disentanglement we call mechanism sparsity regularization, which applies when the latent factors of interest depend sparsely on observed auxiliary variables and/or past latent factors. We propose a representation learning method that induces disentanglement by simultaneously learning the latent factors and the sparse causal graphical model that explains them. We develop a nonparametric identifiability theory that formalizes this principle and shows that the latent factors can be recovered by regularizing the learned causal graph to be sparse. More precisely, we show identifiablity up to a novel equivalence relation we call "consistency", which allows some latent factors to remain entangled (hence the term partial disentanglement). To describe the structure of this entanglement, we introduce the notions of entanglement graphs and graph preserving functions. We further provide a graphical criterion which guarantees complete disentanglement, that is identifiability up to permutations and element-wise transformations. We demonstrate the scope of the mechanism sparsity principle as well as the assumptions it relies on with several worked out examples. For instance, the framework shows how one can leverage multi-node interventions with unknown targets on the latent factors to disentangle them. We further draw connections between our nonparametric results and the now popular exponential family assumption. Lastly, we propose an estimation procedure based on variational autoencoders and a sparsity constraint and demonstrate it on various synthetic datasets. This work is meant to be a significantly extended version of Lachapelle et al. (2022).

Convergence Rates for the MAP of an Exponential Family and Stochastic Mirror Descent -- an Open Problem

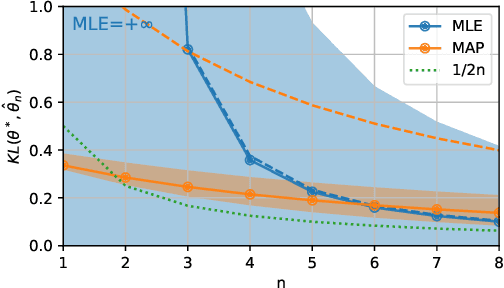
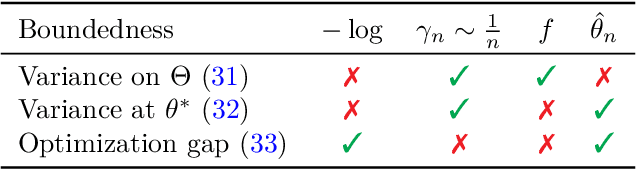
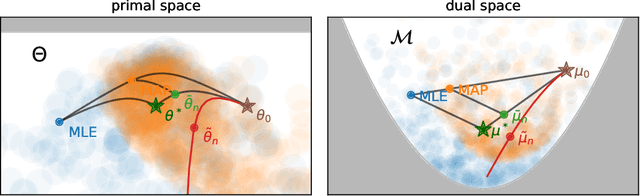
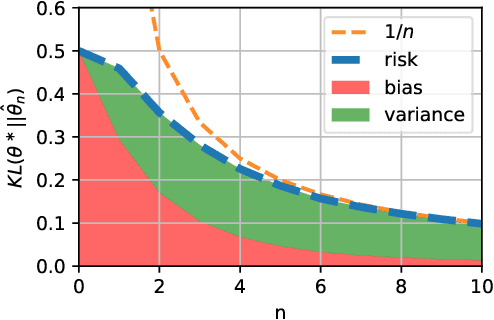
We consider the problem of upper bounding the expected log-likelihood sub-optimality of the maximum likelihood estimate (MLE), or a conjugate maximum a posteriori (MAP) for an exponential family, in a non-asymptotic way. Surprisingly, we found no general solution to this problem in the literature. In particular, current theories do not hold for a Gaussian or in the interesting few samples regime. After exhibiting various facets of the problem, we show we can interpret the MAP as running stochastic mirror descent (SMD) on the log-likelihood. However, modern convergence results do not apply for standard examples of the exponential family, highlighting holes in the convergence literature. We believe solving this very fundamental problem may bring progress to both the statistics and optimization communities.

Discovering Latent Causal Variables via Mechanism Sparsity: A New Principle for Nonlinear ICA

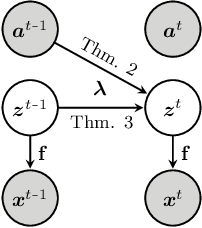
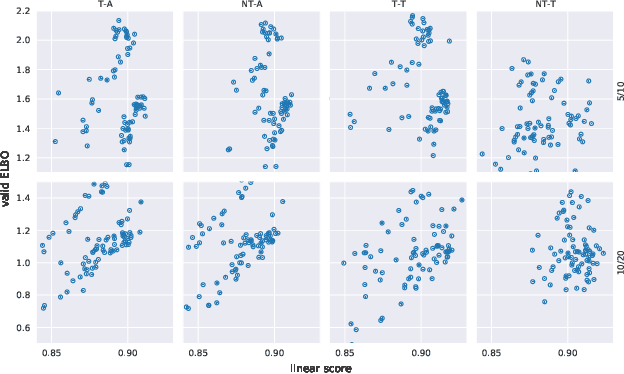
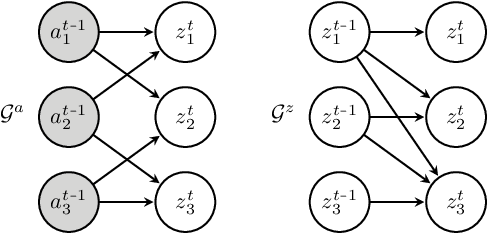
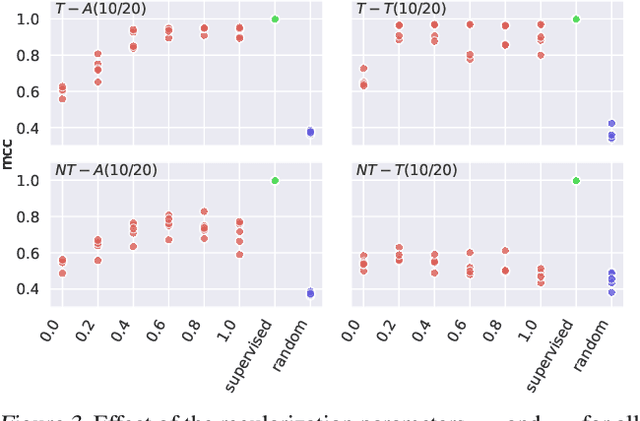
It can be argued that finding an interpretable low-dimensional representation of a potentially high-dimensional phenomenon is central to the scientific enterprise. Independent component analysis (ICA) refers to an ensemble of methods which formalize this goal and provide estimation procedure for practical application. This work proposes mechanism sparsity regularization as a new principle to achieve nonlinear ICA when latent factors depend sparsely on observed auxiliary variables and/or past latent factors. We show that the latent variables can be recovered up to a permutation if one regularizes the latent mechanisms to be sparse and if some graphical criterion is satisfied by the data generating process. As a special case, our framework shows how one can leverage unknown-target interventions on the latent factors to disentangle them, thus drawing further connections between ICA and causality. We validate our theoretical results with toy experiments.

An Analysis of the Adaptation Speed of Causal Models

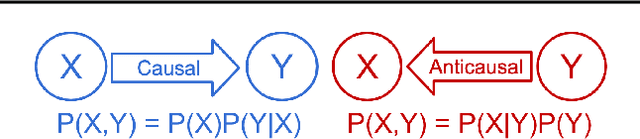
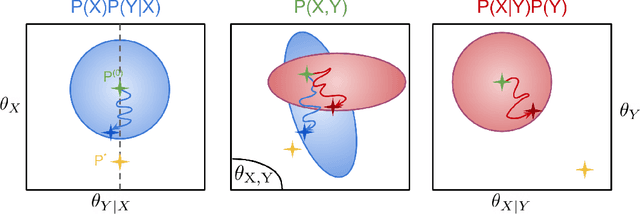
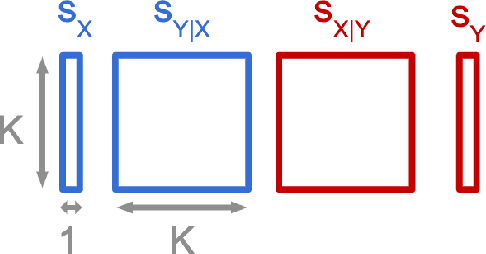
We consider the problem of discovering the causal process that generated a collection of datasets. We assume that all these datasets were generated by unknown sparse interventions on a structural causal model (SCM) $G$, that we want to identify. Recently, Bengio et al. (2020) argued that among all SCMs, $G$ is the fastest to adapt from one dataset to another, and proposed a meta-learning criterion to identify the causal direction in a two-variable SCM. While the experiments were promising, the theoretical justification was incomplete. Our contribution is a theoretical investigation of the adaptation speed of simple two-variable SCMs. We use convergence rates from stochastic optimization to justify that a relevant proxy for adaptation speed is distance in parameter space after intervention. Using this proxy, we show that the SCM with the correct causal direction is advantaged for categorical and normal cause-effect datasets when the intervention is on the cause variable. When the intervention is on the effect variable, we provide a more nuanced picture which highlights that the fastest-to-adapt heuristic is not always valid. Code to reproduce experiments is available at https://github.com/remilepriol/causal-adaptation-speed

Adaptive Stochastic Dual Coordinate Ascent for Conditional Random Fields

This work investigates the training of conditional random fields (CRFs) via the stochastic dual coordinate ascent (SDCA) algorithm of Shalev-Shwartz and Zhang (2016). SDCA enjoys a linear convergence rate and a strong empirical performance for binary classification problems. However, it has never been used to train CRFs. Yet it benefits from an `exact' line search with a single marginalization oracle call, unlike previous approaches. In this paper, we adapt SDCA to train CRFs, and we enhance it with an adaptive non-uniform sampling strategy based on block duality gaps. We perform experiments on four standard sequence prediction tasks. SDCA demonstrates performances on par with the state of the art, and improves over it on three of the four datasets, which have in common the use of sparse features.