An Analysis of the Adaptation Speed of Causal Models

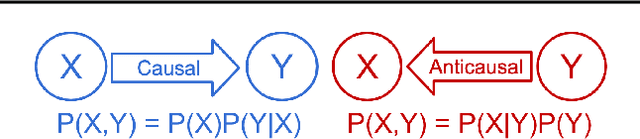
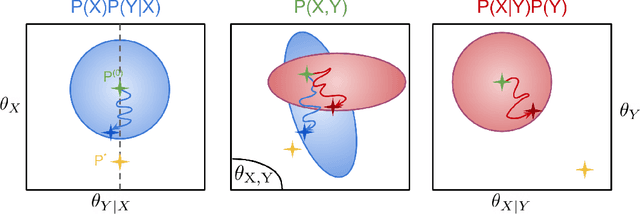
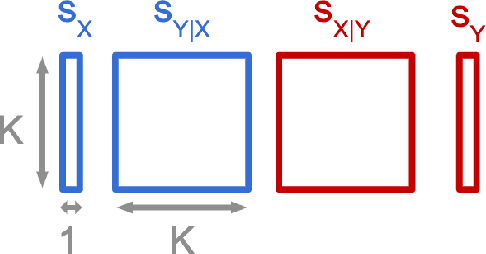
We consider the problem of discovering the causal process that generated a collection of datasets. We assume that all these datasets were generated by unknown sparse interventions on a structural causal model (SCM) $G$, that we want to identify. Recently, Bengio et al. (2020) argued that among all SCMs, $G$ is the fastest to adapt from one dataset to another, and proposed a meta-learning criterion to identify the causal direction in a two-variable SCM. While the experiments were promising, the theoretical justification was incomplete. Our contribution is a theoretical investigation of the adaptation speed of simple two-variable SCMs. We use convergence rates from stochastic optimization to justify that a relevant proxy for adaptation speed is distance in parameter space after intervention. Using this proxy, we show that the SCM with the correct causal direction is advantaged for categorical and normal cause-effect datasets when the intervention is on the cause variable. When the intervention is on the effect variable, we provide a more nuanced picture which highlights that the fastest-to-adapt heuristic is not always valid. Code to reproduce experiments is available at https://github.com/remilepriol/causal-adaptation-speed