Iterative Methods via Locally Evolving Set Process

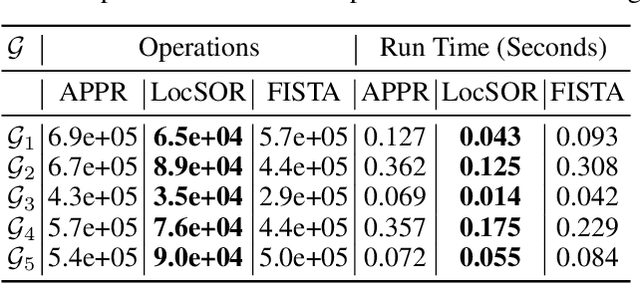
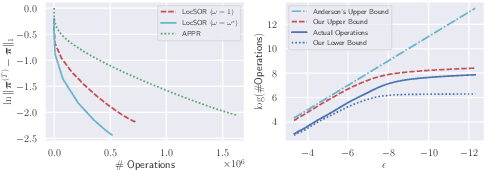
Given the damping factor $\alpha$ and precision tolerance $\epsilon$, \citet{andersen2006local} introduced Approximate Personalized PageRank (APPR), the \textit{de facto local method} for approximating the PPR vector, with runtime bounded by $\Theta(1/(\alpha\epsilon))$ independent of the graph size. Recently, \citet{fountoulakis2022open} asked whether faster local algorithms could be developed using $\tilde{O}(1/(\sqrt{\alpha}\epsilon))$ operations. By noticing that APPR is a local variant of Gauss-Seidel, this paper explores the question of \textit{whether standard iterative solvers can be effectively localized}. We propose to use the \textit{locally evolving set process}, a novel framework to characterize the algorithm locality, and demonstrate that many standard solvers can be effectively localized. Let $\overline{\operatorname{vol}}{ (S_t)}$ and $\overline{\gamma}_{t}$ be the running average of volume and the residual ratio of active nodes $\textstyle S_{t}$ during the process. We show $\overline{\operatorname{vol}}{ (S_t)}/\overline{\gamma}_{t} \leq 1/\epsilon$ and prove APPR admits a new runtime bound $\tilde{O}(\overline{\operatorname{vol}}(S_t)/(\alpha\overline{\gamma}_{t}))$ mirroring the actual performance. Furthermore, when the geometric mean of residual reduction is $\Theta(\sqrt{\alpha})$, then there exists $c \in (0,2)$ such that the local Chebyshev method has runtime $\tilde{O}(\overline{\operatorname{vol}}(S_{t})/(\sqrt{\alpha}(2-c)))$ without the monotonicity assumption. Numerical results confirm the efficiency of this novel framework and show up to a hundredfold speedup over corresponding standard solvers on real-world graphs.

Promoting Exploration in Memory-Augmented Adam using Critical Momenta

Adaptive gradient-based optimizers, particularly Adam, have left their mark in training large-scale deep learning models. The strength of such optimizers is that they exhibit fast convergence while being more robust to hyperparameter choice. However, they often generalize worse than non-adaptive methods. Recent studies have tied this performance gap to flat minima selection: adaptive methods tend to find solutions in sharper basins of the loss landscape, which in turn hurts generalization. To overcome this issue, we propose a new memory-augmented version of Adam that promotes exploration towards flatter minima by using a buffer of critical momentum terms during training. Intuitively, the use of the buffer makes the optimizer overshoot outside the basin of attraction if it is not wide enough. We empirically show that our method improves the performance of several variants of Adam on standard supervised language modelling and image classification tasks.

An Analysis of the Adaptation Speed of Causal Models

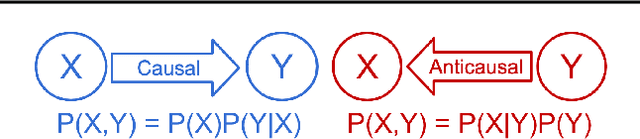
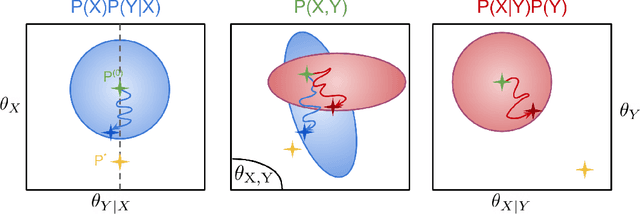
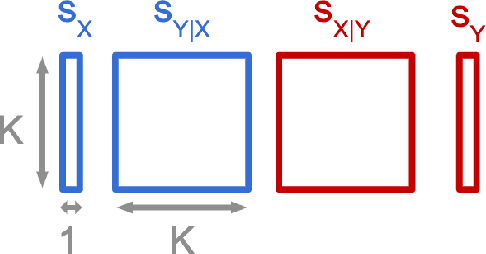
We consider the problem of discovering the causal process that generated a collection of datasets. We assume that all these datasets were generated by unknown sparse interventions on a structural causal model (SCM) $G$, that we want to identify. Recently, Bengio et al. (2020) argued that among all SCMs, $G$ is the fastest to adapt from one dataset to another, and proposed a meta-learning criterion to identify the causal direction in a two-variable SCM. While the experiments were promising, the theoretical justification was incomplete. Our contribution is a theoretical investigation of the adaptation speed of simple two-variable SCMs. We use convergence rates from stochastic optimization to justify that a relevant proxy for adaptation speed is distance in parameter space after intervention. Using this proxy, we show that the SCM with the correct causal direction is advantaged for categorical and normal cause-effect datasets when the intervention is on the cause variable. When the intervention is on the effect variable, we provide a more nuanced picture which highlights that the fastest-to-adapt heuristic is not always valid. Code to reproduce experiments is available at https://github.com/remilepriol/causal-adaptation-speed