Jerry Huang
Beyond Hard Writes and Rigid Preservation: Soft Recursive Least-Squares for Lifelong LLM Editing
Jan 22, 2026Abstract:Model editing updates a pre-trained LLM with new facts or rules without re-training, while preserving unrelated behavior. In real deployment, edits arrive as long streams, and existing editors often face a plasticity-stability dilemma: locate-then-edit "hard writes" can accumulate interference over time, while null-space-style "hard preservation" preserves only what is explicitly constrained, so past edits can be overwritten and unconstrained behaviors may deviate, degrading general capabilities in the many-edits regime. We propose RLSEdit, a recursive least-squares editor for long sequential editing. RLSEdit formulates editing as an online quadratic optimization with soft constraints, minimizing a cumulative key-value fitting objective with two regularizers that control for both deviation from the pre-trained weights and from a designated anchor mapping. The resulting update admits an efficient online recursion via the Woodbury identity, with per-edit cost independent of history length and scaling only with the current edit size. We further provide deviation bounds and an asymptotic characterization of the adherence-preservation trade-off in the many-edits regime. Experiments on multiple model families demonstrate stable scaling to 10K edits, outperforming strong baselines in both edit success and holistic stability -- crucially retaining early edits, and preserving general capabilities on GLUE and held-out reasoning/code benchmarks.
Investigating the Multilingual Calibration Effects of Language Model Instruction-Tuning
Jan 04, 2026Abstract:Ensuring that deep learning models are well-calibrated in terms of their predictive uncertainty is essential in maintaining their trustworthiness and reliability, yet despite increasing advances in foundation model research, the relationship between such large language models (LLMs) and their calibration remains an open area of research. In this work, we look at a critical gap in the calibration of LLMs within multilingual settings, in an attempt to better understand how the data scarcity can potentially lead to different calibration effects and how commonly used techniques can apply in these settings. Our analysis on two multilingual benchmarks, over 29 and 42 languages respectively, reveals that even in low-resource languages, model confidence can increase significantly after instruction-tuning on high-resource language SFT datasets. However, improvements in accuracy are marginal or non-existent, resulting in mis-calibration, highlighting a critical shortcoming of standard SFT for multilingual languages. Furthermore, we observe that the use of label smoothing to be a reasonable method alleviate this concern, again without any need for low-resource SFT data, maintaining better calibration across all languages. Overall, this highlights the importance of multilingual considerations for both training and tuning LLMs in order to improve their reliability and fairness in downstream use.
Audited Skill-Graph Self-Improvement for Agentic LLMs via Verifiable Rewards, Experience Synthesis, and Continual Memory
Dec 28, 2025Abstract:Reinforcement learning is increasingly used to transform large language models into agentic systems that act over long horizons, invoke tools, and manage memory under partial observability. While recent work has demonstrated performance gains through tool learning, verifiable rewards, and continual training, deployed self-improving agents raise unresolved security and governance challenges: optimization pressure can incentivize reward hacking, behavioral drift is difficult to audit or reproduce, and improvements are often entangled in opaque parameter updates rather than reusable, verifiable artifacts. This paper proposes Audited Skill-Graph Self-Improvement (ASG-SI), a framework that treats self-improvement as iterative compilation of an agent into a growing, auditable skill graph. Each candidate improvement is extracted from successful trajectories, normalized into a skill with an explicit interface, and promoted only after passing verifier-backed replay and contract checks. Rewards are decomposed into reconstructible components derived from replayable evidence, enabling independent audit of promotion decisions and learning signals. ASG-SI further integrates experience synthesis for scalable stress testing and continual memory control to preserve long-horizon performance under bounded context. We present a complete system architecture, threat model, and security analysis, and provide a fully runnable reference implementation that demonstrates verifier-backed reward construction, skill compilation, audit logging, and measurable improvement under continual task streams. ASG-SI reframes agentic self-improvement as accumulation of verifiable, reusable capabilities, offering a practical path toward reproducible evaluation and operational governance of self-improving AI agents.
Sublinear iterations can suffice even for DDPMs
Nov 06, 2025Abstract:SDE-based methods such as denoising diffusion probabilistic models (DDPMs) have shown remarkable success in real-world sample generation tasks. Prior analyses of DDPMs have been focused on the exponential Euler discretization, showing guarantees that generally depend at least linearly on the dimension or initial Fisher information. Inspired by works in log-concave sampling (Shen and Lee, 2019), we analyze an integrator -- the denoising diffusion randomized midpoint method (DDRaM) -- that leverages an additional randomized midpoint to better approximate the SDE. Using a recently-developed analytic framework called the "shifted composition rule", we show that this algorithm enjoys favorable discretization properties under appropriate smoothness assumptions, with sublinear $\widetilde{O}(\sqrt{d})$ score evaluations needed to ensure convergence. This is the first sublinear complexity bound for pure DDPM sampling -- prior works which obtained such bounds worked instead with ODE-based sampling and had to make modifications to the sampler which deviate from how they are used in practice. We also provide experimental validation of the advantages of our method, showing that it performs well in practice with pre-trained image synthesis models.
AAGATE: A NIST AI RMF-Aligned Governance Platform for Agentic AI
Oct 29, 2025Abstract:This paper introduces the Agentic AI Governance Assurance & Trust Engine (AAGATE), a Kubernetes-native control plane designed to address the unique security and governance challenges posed by autonomous, language-model-driven agents in production. Recognizing the limitations of traditional Application Security (AppSec) tooling for improvisational, machine-speed systems, AAGATE operationalizes the NIST AI Risk Management Framework (AI RMF). It integrates specialized security frameworks for each RMF function: the Agentic AI Threat Modeling MAESTRO framework for Map, a hybrid of OWASP's AIVSS and SEI's SSVC for Measure, and the Cloud Security Alliance's Agentic AI Red Teaming Guide for Manage. By incorporating a zero-trust service mesh, an explainable policy engine, behavioral analytics, and decentralized accountability hooks, AAGATE provides a continuous, verifiable governance solution for agentic AI, enabling safe, accountable, and scalable deployment. The framework is further extended with DIRF for digital identity rights, LPCI defenses for logic-layer injection, and QSAF monitors for cognitive degradation, ensuring governance spans systemic, adversarial, and ethical risks.
Lifetime-Aware Design of Item-Level Intelligence
Sep 09, 2025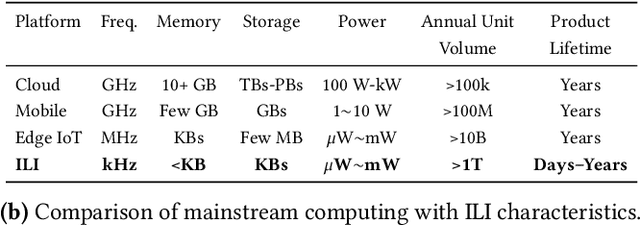


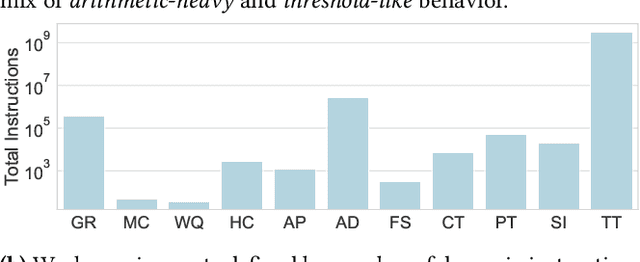
Abstract:We present FlexiFlow, a lifetime-aware design framework for item-level intelligence (ILI) where computation is integrated directly into disposable products like food packaging and medical patches. Our framework leverages natively flexible electronics which offer significantly lower costs than silicon but are limited to kHz speeds and several thousands of gates. Our insight is that unlike traditional computing with more uniform deployment patterns, ILI applications exhibit 1000X variation in operational lifetime, fundamentally changing optimal architectural design decisions when considering trillion-item deployment scales. To enable holistic design and optimization, we model the trade-offs between embodied carbon footprint and operational carbon footprint based on application-specific lifetimes. The framework includes: (1) FlexiBench, a workload suite targeting sustainability applications from spoilage detection to health monitoring; (2) FlexiBits, area-optimized RISC-V cores with 1/4/8-bit datapaths achieving 2.65X to 3.50X better energy efficiency per workload execution; and (3) a carbon-aware model that selects optimal architectures based on deployment characteristics. We show that lifetime-aware microarchitectural design can reduce carbon footprint by 1.62X, while algorithmic decisions can reduce carbon footprint by 14.5X. We validate our approach through the first tape-out using a PDK for flexible electronics with fully open-source tools, achieving 30.9kHz operation. FlexiFlow enables exploration of computing at the Extreme Edge where conventional design methodologies must be reevaluated to account for new constraints and considerations.
Fortifying the Agentic Web: A Unified Zero-Trust Architecture Against Logic-layer Threats
Aug 17, 2025Abstract:This paper presents a Unified Security Architecture that fortifies the Agentic Web through a Zero-Trust IAM framework. This architecture is built on a foundation of rich, verifiable agent identities using Decentralized Identifiers (DIDs) and Verifiable Credentials (VCs), with discovery managed by a protocol-agnostic Agent Name Service (ANS). Security is operationalized through a multi-layered Trust Fabric which introduces significant innovations, including Trust-Adaptive Runtime Environments (TARE), Causal Chain Auditing, and Dynamic Identity with Behavioral Attestation. By explicitly linking the LPCI threat to these enhanced architectural countermeasures within a formal security model, we propose a comprehensive and forward-looking blueprint for a secure, resilient, and trustworthy agentic ecosystem. Our formal analysis demonstrates that the proposed architecture provides provable security guarantees against LPCI attacks with bounded probability of success.
Parity Requires Unified Input Dependence and Negative Eigenvalues in SSMs
Aug 10, 2025Abstract:Recent work has shown that LRNN models such as S4D, Mamba, and DeltaNet lack state-tracking capability due to either time-invariant transition matrices or restricted eigenvalue ranges. To address this, input-dependent transition matrices, particularly those that are complex or non-triangular, have been proposed to enhance SSM performance on such tasks. While existing theorems demonstrate that both input-independent and non-negative SSMs are incapable of solving simple state-tracking tasks, such as parity, regardless of depth, they do not explore whether combining these two types in a multilayer SSM could help. We investigate this question for efficient SSMs with diagonal transition matrices and show that such combinations still fail to solve parity. This implies that a recurrence layer must both be input-dependent and include negative eigenvalues. Our experiments support this conclusion by analyzing an SSM model that combines S4D and Mamba layers.
Calibrated Language Models and How to Find Them with Label Smoothing
Aug 01, 2025Abstract:Recent advances in natural language processing (NLP) have opened up greater opportunities to enable fine-tuned large language models (LLMs) to behave as more powerful interactive agents through improved instruction-following ability. However, understanding how this impacts confidence calibration for reliable model output has not been researched in full. In this work, we examine various open-sourced LLMs, identifying significant calibration degradation after instruction tuning in each. Seeking a practical solution, we look towards label smoothing, which has been shown as an effective method to regularize for overconfident predictions but has yet to be widely adopted in the supervised fine-tuning (SFT) of LLMs. We first provide insight as to why label smoothing is sufficient to maintain calibration throughout the SFT process. However, settings remain where the effectiveness of smoothing is severely diminished, in particular the case of large vocabulary LLMs (LV-LLMs). We posit the cause to stem from the ability to become over-confident, which has a direct relationship with the hidden size and vocabulary size, and justify this theoretically and experimentally. Finally, we address an outstanding issue regarding the memory footprint of the cross-entropy loss computation in the label smoothed loss setting, designing a customized kernel to dramatically reduce memory consumption without sacrificing speed or performance in comparison to existing solutions for non-smoothed losses.
PoTPTQ: A Two-step Power-of-Two Post-training for LLMs
Jul 16, 2025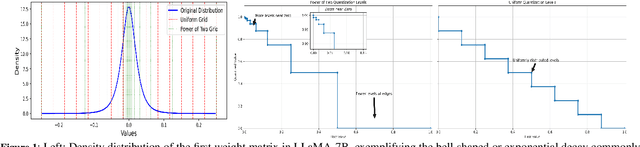
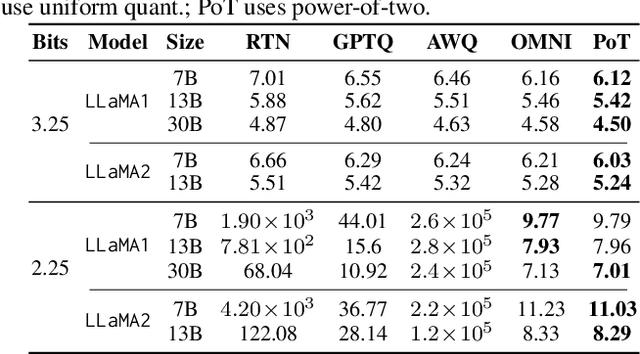
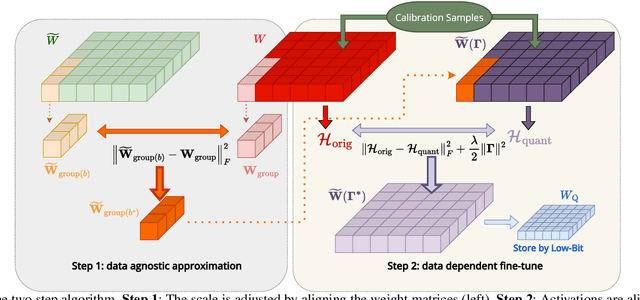
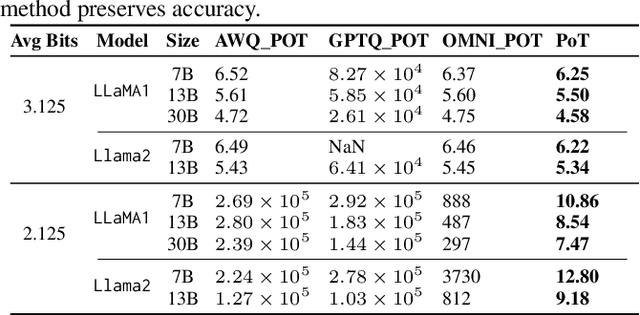
Abstract:Large Language Models (LLMs) have demonstrated remarkable performance across various natural language processing (NLP) tasks. However, their deployment is challenging due to the substantial computational resources required. Power-of-two (PoT) quantization is a general tool to counteract this difficulty. Albeit previous works on PoT quantization can be efficiently dequantized on CPUs using fixed-point addition, it showed less effectiveness on GPUs. The reason is entanglement of the sign bit and sequential bit manipulations needed for dequantization. We propose a novel POT quantization framework for LLM weights that (i) outperforms state-of-the-art accuracy in extremely low-precision number formats, and (ii) enables faster inference through more efficient dequantization. To maintain the accuracy of the quantized model, we introduce a two-step post-training algorithm: (i) initialize the quantization scales with a robust starting point, and (ii) refine these scales using a minimal calibration set. The performance of our PoT post-training algorithm surpasses the current state-of-the-art in integer quantization, particularly at low precisions such as 2- and 3-bit formats. Our PoT quantization accelerates the dequantization step required for the floating point inference and leads to $3.67\times$ speed up on a NVIDIA V100, and $1.63\times$ on a NVIDIA RTX 4090, compared to uniform integer dequantization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge