Xiao-Wen Chang
PoTPTQ: A Two-step Power-of-Two Post-training for LLMs
Jul 16, 2025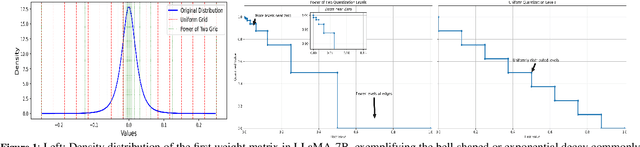
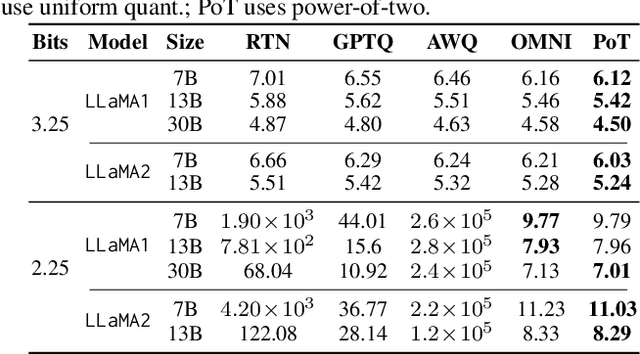
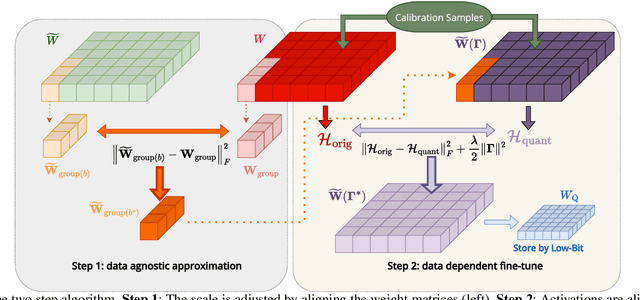
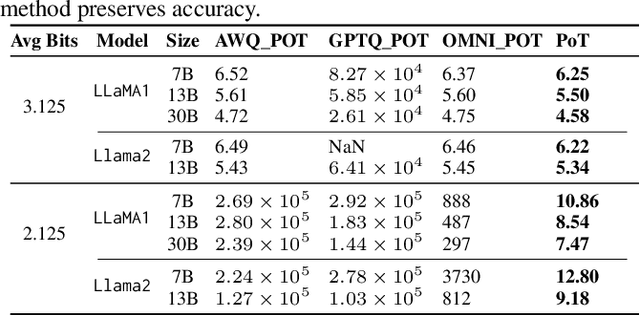
Abstract:Large Language Models (LLMs) have demonstrated remarkable performance across various natural language processing (NLP) tasks. However, their deployment is challenging due to the substantial computational resources required. Power-of-two (PoT) quantization is a general tool to counteract this difficulty. Albeit previous works on PoT quantization can be efficiently dequantized on CPUs using fixed-point addition, it showed less effectiveness on GPUs. The reason is entanglement of the sign bit and sequential bit manipulations needed for dequantization. We propose a novel POT quantization framework for LLM weights that (i) outperforms state-of-the-art accuracy in extremely low-precision number formats, and (ii) enables faster inference through more efficient dequantization. To maintain the accuracy of the quantized model, we introduce a two-step post-training algorithm: (i) initialize the quantization scales with a robust starting point, and (ii) refine these scales using a minimal calibration set. The performance of our PoT post-training algorithm surpasses the current state-of-the-art in integer quantization, particularly at low precisions such as 2- and 3-bit formats. Our PoT quantization accelerates the dequantization step required for the floating point inference and leads to $3.67\times$ speed up on a NVIDIA V100, and $1.63\times$ on a NVIDIA RTX 4090, compared to uniform integer dequantization.
SCAR: Shapley Credit Assignment for More Efficient RLHF
May 26, 2025Abstract:Reinforcement Learning from Human Feedback (RLHF) is a widely used technique for aligning Large Language Models (LLMs) with human preferences, yet it often suffers from sparse reward signals, making effective credit assignment challenging. In typical setups, the reward model provides a single scalar score for an entire generated sequence, offering little insight into which token or span-level decisions were responsible for the outcome. To address this, we propose Shapley Credit Assignment Rewards (SCAR), a novel method that leverages Shapley values in cooperative game theory. SCAR distributes the total sequence-level reward among constituent tokens or text spans based on their principled marginal contributions. This creates dense reward signals, crucially, without necessitating the training of auxiliary critique models or recourse to fine-grained human annotations at intermediate generation stages. Unlike prior dense reward methods, SCAR offers a game-theoretic foundation for fair credit attribution. Theoretically, we demonstrate that SCAR preserves the original optimal policy, and empirically, across diverse tasks including sentiment control, text summarization, and instruction tuning, we show that SCAR converges significantly faster and achieves higher final reward scores compared to standard RLHF and attention-based dense reward baselines. Our findings suggest that SCAR provides a more effective and theoretically sound method for credit assignment in RLHF, leading to more efficient alignment of LLMs.
Resona: Improving Context Copying in Linear Recurrence Models with Retrieval
Mar 28, 2025Abstract:Recent shifts in the space of large language model (LLM) research have shown an increasing focus on novel architectures to compete with prototypical Transformer-based models that have long dominated this space. Linear recurrent models have proven to be a viable competitor due to their computational efficiency. However, such models still demonstrate a sizable gap compared to Transformers in terms of in-context learning among other tasks that require recalling information from a context. In this work, we introduce __Resona__, a simple and scalable framework for augmenting linear recurrent models with retrieval. __Resona__~augments models with the ability to integrate retrieved information from the provided input context, enabling tailored behavior to diverse task requirements. Experiments on a variety of linear recurrent models demonstrate that __Resona__-augmented models observe significant performance gains on a variety of synthetic as well as real-world natural language tasks, highlighting its ability to act as a general purpose method to improve the in-context learning and language modeling abilities of linear recurrent LLMs.
Flexible Diffusion Scopes with Parameterized Laplacian for Heterophilic Graph Learning
Sep 15, 2024



Abstract:The ability of Graph Neural Networks (GNNs) to capture long-range and global topology information is limited by the scope of conventional graph Laplacian, leading to unsatisfactory performance on some datasets, particularly on heterophilic graphs. To address this limitation, we propose a new class of parameterized Laplacian matrices, which provably offers more flexibility in controlling the diffusion distance between nodes than the conventional graph Laplacian, allowing long-range information to be adaptively captured through diffusion on graph. Specifically, we first prove that the diffusion distance and spectral distance on graph have an order-preserving relationship. With this result, we demonstrate that the parameterized Laplacian can accelerate the diffusion of long-range information, and the parameters in the Laplacian enable flexibility of the diffusion scopes. Based on the theoretical results, we propose topology-guided rewiring mechanism to capture helpful long-range neighborhood information for heterophilic graphs. With this mechanism and the new Laplacian, we propose two GNNs with flexible diffusion scopes: namely the Parameterized Diffusion based Graph Convolutional Networks (PD-GCN) and Graph Attention Networks (PD-GAT). Synthetic experiments reveal the high correlations between the parameters of the new Laplacian and the performance of parameterized GNNs under various graph homophily levels, which verifies that our new proposed GNNs indeed have the ability to adjust the parameters to adaptively capture the global information for different levels of heterophilic graphs. They also outperform the state-of-the-art (SOTA) models on 6 out of 7 real-world benchmark datasets, which further confirms their superiority.
Are Heterophily-Specific GNNs and Homophily Metrics Really Effective? Evaluation Pitfalls and New Benchmarks
Sep 09, 2024



Abstract:Over the past decade, Graph Neural Networks (GNNs) have achieved great success on machine learning tasks with relational data. However, recent studies have found that heterophily can cause significant performance degradation of GNNs, especially on node-level tasks. Numerous heterophilic benchmark datasets have been put forward to validate the efficacy of heterophily-specific GNNs and various homophily metrics have been designed to help people recognize these malignant datasets. Nevertheless, there still exist multiple pitfalls that severely hinder the proper evaluation of new models and metrics. In this paper, we point out three most serious pitfalls: 1) a lack of hyperparameter tuning; 2) insufficient model evaluation on the real challenging heterophilic datasets; 3) missing quantitative evaluation benchmark for homophily metrics on synthetic graphs. To overcome these challenges, we first train and fine-tune baseline models on $27$ most widely used benchmark datasets, categorize them into three distinct groups: malignant, benign and ambiguous heterophilic datasets, and identify the real challenging subsets of tasks. To our best knowledge, we are the first to propose such taxonomy. Then, we re-evaluate $10$ heterophily-specific state-of-the-arts (SOTA) GNNs with fine-tuned hyperparameters on different groups of heterophilic datasets. Based on the model performance, we reassess their effectiveness on addressing heterophily challenge. At last, we evaluate $11$ popular homophily metrics on synthetic graphs with three different generation approaches. To compare the metrics strictly, we propose the first quantitative evaluation method based on Fr\'echet distance.
The Heterophilic Graph Learning Handbook: Benchmarks, Models, Theoretical Analysis, Applications and Challenges
Jul 12, 2024



Abstract:Homophily principle, \ie{} nodes with the same labels or similar attributes are more likely to be connected, has been commonly believed to be the main reason for the superiority of Graph Neural Networks (GNNs) over traditional Neural Networks (NNs) on graph-structured data, especially on node-level tasks. However, recent work has identified a non-trivial set of datasets where GNN's performance compared to the NN's is not satisfactory. Heterophily, i.e. low homophily, has been considered the main cause of this empirical observation. People have begun to revisit and re-evaluate most existing graph models, including graph transformer and its variants, in the heterophily scenario across various kinds of graphs, e.g. heterogeneous graphs, temporal graphs and hypergraphs. Moreover, numerous graph-related applications are found to be closely related to the heterophily problem. In the past few years, considerable effort has been devoted to studying and addressing the heterophily issue. In this survey, we provide a comprehensive review of the latest progress on heterophilic graph learning, including an extensive summary of benchmark datasets and evaluation of homophily metrics on synthetic graphs, meticulous classification of the most updated supervised and unsupervised learning methods, thorough digestion of the theoretical analysis on homophily/heterophily, and broad exploration of the heterophily-related applications. Notably, through detailed experiments, we are the first to categorize benchmark heterophilic datasets into three sub-categories: malignant, benign and ambiguous heterophily. Malignant and ambiguous datasets are identified as the real challenging datasets to test the effectiveness of new models on the heterophily challenge. Finally, we propose several challenges and future directions for heterophilic graph representation learning.
GCEPNet: Graph Convolution-Enhanced Expectation Propagation for Massive MIMO Detection
Apr 23, 2024


Abstract:Massive MIMO (multiple-input multiple-output) detection is an important topic in wireless communication and various machine learning based methods have been developed recently for this task. Expectation propagation (EP) and its variants are widely used for MIMO detection and have achieved the best performance. However, EP-based solvers fail to capture the correlation between unknown variables, leading to loss of information, and in addition, they are computationally expensive. In this paper, we show that the real-valued system can be modeled as spectral signal convolution on graph, through which the correlation between unknown variables can be captured. Based on this analysis, we propose graph convolution-enhanced expectation propagation (GCEPNet), a graph convolution-enhanced EP detector. GCEPNet incorporates data-dependent attention scores into Chebyshev polynomial for powerful graph convolution with better generalization capacity. It enables a better estimation of the cavity distribution for EP and empirically achieves the state-of-the-art (SOTA) MIMO detection performance with much faster inference speed. To our knowledge, we are the first to shed light on the connection between the system model and graph convolution, and the first to design the data-dependent attention scores for graph convolution.
Representation Learning on Heterophilic Graph with Directional Neighborhood Attention
Mar 03, 2024



Abstract:Graph Attention Network (GAT) is one of the most popular Graph Neural Network (GNN) architecture, which employs the attention mechanism to learn edge weights and has demonstrated promising performance in various applications. However, since it only incorporates information from immediate neighborhood, it lacks the ability to capture long-range and global graph information, leading to unsatisfactory performance on some datasets, particularly on heterophilic graphs. To address this limitation, we propose the Directional Graph Attention Network (DGAT) in this paper. DGAT is able to combine the feature-based attention with the global directional information extracted from the graph topology. To this end, a new class of Laplacian matrices is proposed which can provably reduce the diffusion distance between nodes. Based on the new Laplacian, topology-guided neighbour pruning and edge adding mechanisms are proposed to remove the noisy and capture the helpful long-range neighborhood information. Besides, a global directional attention is designed to enable a topological-aware information propagation. The superiority of the proposed DGAT over the baseline GAT has also been verified through experiments on real-world benchmarks and synthetic data sets. It also outperforms the state-of-the-art (SOTA) models on 6 out of 7 real-world benchmark datasets.
Success probability of the $L_0$-regularized box-constrained Babai point and column permutation strategies
Jan 29, 2024Abstract:We consider the success probability of the $L_0$-regularized box-constrained Babai point, which is a suboptimal solution to the $L_0$-regularized box-constrained integer least squares problem and can be used for MIMO detection. First, we derive formulas for the success probability of both $L_0$-regularized and unregularized box-constrained Babai points. Then we investigate the properties of the $L_0$-regularized box-constrained Babai point, including the optimality of the regularization parameter, the monotonicity of its success probability, and the monotonicity of the ratio of the two success probabilities. A bound on the success probability of the $L_0$-regularized Babai point is derived. After that, we analyze the effect of the LLL-P permutation strategy on the success probability of the $L_0$-regularized Babai point. Then we propose some success probability based column permutation strategies to increase the success probability of the $L_0$-regularized box-constrained Babai point. Finally, we present numerical tests to confirm our theoretical results and to show the advantage of the $L_0$ regularization and the effectiveness of the proposed column permutation algorithms compared to existing strategies.
When Do Graph Neural Networks Help with Node Classification: Investigating the Homophily Principle on Node Distinguishability
Apr 25, 2023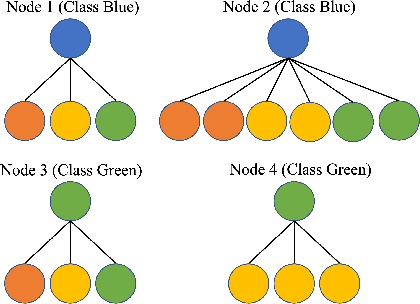
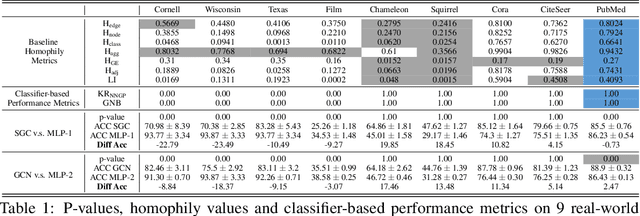
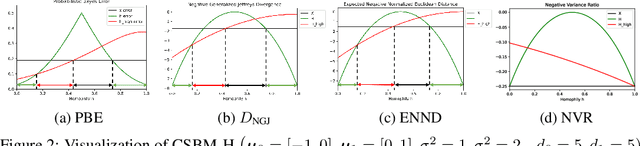
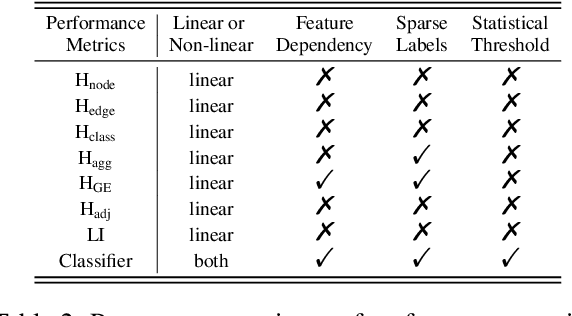
Abstract:Homophily principle, i.e. nodes with the same labels are more likely to be connected, was believed to be the main reason for the performance superiority of Graph Neural Networks (GNNs) over Neural Networks (NNs) on Node Classification (NC) tasks. Recently, people have developed theoretical results arguing that, even though the homophily principle is broken, the advantage of GNNs can still hold as long as nodes from the same class share similar neighborhood patterns, which questions the validity of homophily. However, this argument only considers intra-class Node Distinguishability (ND) and ignores inter-class ND, which is insufficient to study the effect of homophily. In this paper, we first demonstrate the aforementioned insufficiency with examples and argue that an ideal situation for ND is to have smaller intra-class ND than inter-class ND. To formulate this idea and have a better understanding of homophily, we propose Contextual Stochastic Block Model for Homophily (CSBM-H) and define two metrics, Probabilistic Bayes Error (PBE) and Expected Negative KL-divergence (ENKL), to quantify ND, through which we can also find how intra- and inter-class ND influence ND together. We visualize the results and give detailed analysis. Through experiments, we verified that the superiority of GNNs is indeed closely related to both intra- and inter-class ND regardless of homophily levels, based on which we define Kernel Performance Metric (KPM). KPM is a new non-linear, feature-based metric, which is tested to be more effective than the existing homophily metrics on revealing the advantage and disadvantage of GNNs on synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge