Reaction-conditioned De Novo Enzyme Design with GENzyme

The introduction of models like RFDiffusionAA, AlphaFold3, AlphaProteo, and Chai1 has revolutionized protein structure modeling and interaction prediction, primarily from a binding perspective, focusing on creating ideal lock-and-key models. However, these methods can fall short for enzyme-substrate interactions, where perfect binding models are rare, and induced fit states are more common. To address this, we shift to a functional perspective for enzyme design, where the enzyme function is defined by the reaction it catalyzes. Here, we introduce \textsc{GENzyme}, a \textit{de novo} enzyme design model that takes a catalytic reaction as input and generates the catalytic pocket, full enzyme structure, and enzyme-substrate binding complex. \textsc{GENzyme} is an end-to-end, three-staged model that integrates (1) a catalytic pocket generation and sequence co-design module, (2) a pocket inpainting and enzyme inverse folding module, and (3) a binding and screening module to optimize and predict enzyme-substrate complexes. The entire design process is driven by the catalytic reaction being targeted. This reaction-first approach allows for more accurate and biologically relevant enzyme design, potentially surpassing structure-based and binding-focused models in creating enzymes capable of catalyzing specific reactions. We provide \textsc{GENzyme} code at https://github.com/WillHua127/GENzyme.

Learning From Graph-Structured Data: Addressing Design Issues and Exploring Practical Applications in Graph Representation Learning

Graphs serve as fundamental descriptors for systems composed of interacting elements, capturing a wide array of data types, from molecular interactions to social networks and knowledge graphs. In this paper, we present an exhaustive review of the latest advancements in graph representation learning and Graph Neural Networks (GNNs). GNNs, tailored to handle graph-structured data, excel in deriving insights and predictions from intricate relational information, making them invaluable for tasks involving such data. Graph representation learning, a pivotal approach in analyzing graph-structured data, facilitates numerous downstream tasks and applications across machine learning, data mining, biomedicine, and healthcare. Our work delves into the capabilities of GNNs, examining their foundational designs and their application in addressing real-world challenges. We introduce a GNN equipped with an advanced high-order pooling function, adept at capturing complex node interactions within graph-structured data. This pooling function significantly enhances the GNN's efficacy in both node- and graph-level tasks. Additionally, we propose a molecular graph generative model with a GNN as its core framework. This GNN backbone is proficient in learning invariant and equivariant molecular characteristics. Employing these features, the molecular graph generative model is capable of simultaneously learning and generating molecular graphs with atom-bond structures and precise atom positions. Our models undergo thorough experimental evaluations and comparisons with established methods, showcasing their superior performance in addressing diverse real-world challenges with various datasets.

Are Heterophily-Specific GNNs and Homophily Metrics Really Effective? Evaluation Pitfalls and New Benchmarks

Over the past decade, Graph Neural Networks (GNNs) have achieved great success on machine learning tasks with relational data. However, recent studies have found that heterophily can cause significant performance degradation of GNNs, especially on node-level tasks. Numerous heterophilic benchmark datasets have been put forward to validate the efficacy of heterophily-specific GNNs and various homophily metrics have been designed to help people recognize these malignant datasets. Nevertheless, there still exist multiple pitfalls that severely hinder the proper evaluation of new models and metrics. In this paper, we point out three most serious pitfalls: 1) a lack of hyperparameter tuning; 2) insufficient model evaluation on the real challenging heterophilic datasets; 3) missing quantitative evaluation benchmark for homophily metrics on synthetic graphs. To overcome these challenges, we first train and fine-tune baseline models on $27$ most widely used benchmark datasets, categorize them into three distinct groups: malignant, benign and ambiguous heterophilic datasets, and identify the real challenging subsets of tasks. To our best knowledge, we are the first to propose such taxonomy. Then, we re-evaluate $10$ heterophily-specific state-of-the-arts (SOTA) GNNs with fine-tuned hyperparameters on different groups of heterophilic datasets. Based on the model performance, we reassess their effectiveness on addressing heterophily challenge. At last, we evaluate $11$ popular homophily metrics on synthetic graphs with three different generation approaches. To compare the metrics strictly, we propose the first quantitative evaluation method based on Fr\'echet distance.

Reactzyme: A Benchmark for Enzyme-Reaction Prediction

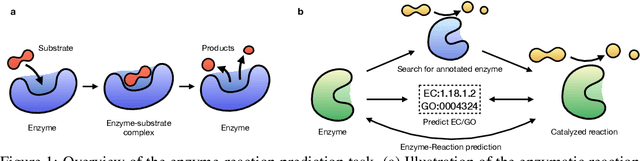
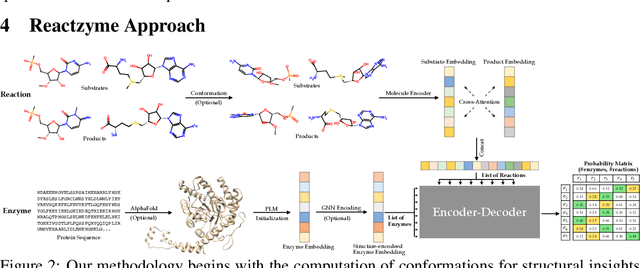
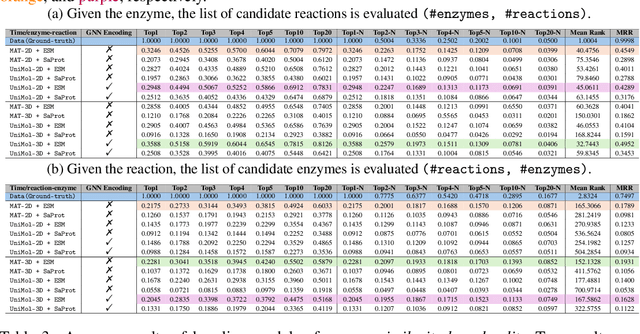
Enzymes, with their specific catalyzed reactions, are necessary for all aspects of life, enabling diverse biological processes and adaptations. Predicting enzyme functions is essential for understanding biological pathways, guiding drug development, enhancing bioproduct yields, and facilitating evolutionary studies. Addressing the inherent complexities, we introduce a new approach to annotating enzymes based on their catalyzed reactions. This method provides detailed insights into specific reactions and is adaptable to newly discovered reactions, diverging from traditional classifications by protein family or expert-derived reaction classes. We employ machine learning algorithms to analyze enzyme reaction datasets, delivering a much more refined view on the functionality of enzymes. Our evaluation leverages the largest enzyme-reaction dataset to date, derived from the SwissProt and Rhea databases with entries up to January 8, 2024. We frame the enzyme-reaction prediction as a retrieval problem, aiming to rank enzymes by their catalytic ability for specific reactions. With our model, we can recruit proteins for novel reactions and predict reactions in novel proteins, facilitating enzyme discovery and function annotation.

The Heterophilic Graph Learning Handbook: Benchmarks, Models, Theoretical Analysis, Applications and Challenges

Homophily principle, \ie{} nodes with the same labels or similar attributes are more likely to be connected, has been commonly believed to be the main reason for the superiority of Graph Neural Networks (GNNs) over traditional Neural Networks (NNs) on graph-structured data, especially on node-level tasks. However, recent work has identified a non-trivial set of datasets where GNN's performance compared to the NN's is not satisfactory. Heterophily, i.e. low homophily, has been considered the main cause of this empirical observation. People have begun to revisit and re-evaluate most existing graph models, including graph transformer and its variants, in the heterophily scenario across various kinds of graphs, e.g. heterogeneous graphs, temporal graphs and hypergraphs. Moreover, numerous graph-related applications are found to be closely related to the heterophily problem. In the past few years, considerable effort has been devoted to studying and addressing the heterophily issue. In this survey, we provide a comprehensive review of the latest progress on heterophilic graph learning, including an extensive summary of benchmark datasets and evaluation of homophily metrics on synthetic graphs, meticulous classification of the most updated supervised and unsupervised learning methods, thorough digestion of the theoretical analysis on homophily/heterophily, and broad exploration of the heterophily-related applications. Notably, through detailed experiments, we are the first to categorize benchmark heterophilic datasets into three sub-categories: malignant, benign and ambiguous heterophily. Malignant and ambiguous datasets are identified as the real challenging datasets to test the effectiveness of new models on the heterophily challenge. Finally, we propose several challenges and future directions for heterophilic graph representation learning.

Effective Protein-Protein Interaction Exploration with PPIretrieval

Protein-protein interactions (PPIs) are crucial in regulating numerous cellular functions, including signal transduction, transportation, and immune defense. As the accuracy of multi-chain protein complex structure prediction improves, the challenge has shifted towards effectively navigating the vast complex universe to identify potential PPIs. Herein, we propose PPIretrieval, the first deep learning-based model for protein-protein interaction exploration, which leverages existing PPI data to effectively search for potential PPIs in an embedding space, capturing rich geometric and chemical information of protein surfaces. When provided with an unseen query protein with its associated binding site, PPIretrieval effectively identifies a potential binding partner along with its corresponding binding site in an embedding space, facilitating the formation of protein-protein complexes.

MUDiff: Unified Diffusion for Complete Molecule Generation

We present a new model for generating molecular data by combining discrete and continuous diffusion processes. Our model generates a comprehensive representation of molecules, including atom features, 2D discrete molecule structures, and 3D continuous molecule coordinates. The use of diffusion processes allows for capturing the probabilistic nature of molecular processes and the ability to explore the effect of different factors on molecular structures and properties. Additionally, we propose a novel graph transformer architecture to denoise the diffusion process. The transformer is equivariant to Euclidean transformations, allowing it to learn invariant atom and edge representations while preserving the equivariance of atom coordinates. This transformer can be used to learn molecular representations robust to geometric transformations. We evaluate the performance of our model through experiments and comparisons with existing methods, showing its ability to generate more stable and valid molecules with good properties. Our model is a promising approach for designing molecules with desired properties and can be applied to a wide range of tasks in molecular modeling.

When Do Graph Neural Networks Help with Node Classification: Investigating the Homophily Principle on Node Distinguishability

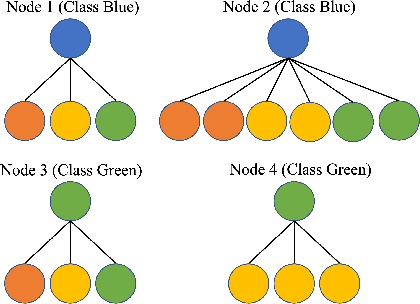
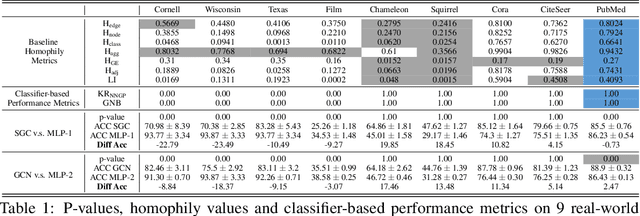
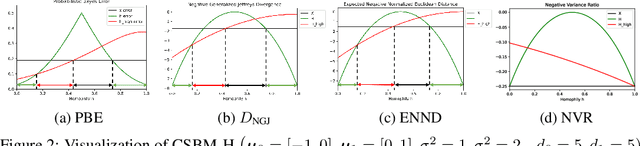
Homophily principle, i.e. nodes with the same labels are more likely to be connected, was believed to be the main reason for the performance superiority of Graph Neural Networks (GNNs) over Neural Networks (NNs) on Node Classification (NC) tasks. Recently, people have developed theoretical results arguing that, even though the homophily principle is broken, the advantage of GNNs can still hold as long as nodes from the same class share similar neighborhood patterns, which questions the validity of homophily. However, this argument only considers intra-class Node Distinguishability (ND) and ignores inter-class ND, which is insufficient to study the effect of homophily. In this paper, we first demonstrate the aforementioned insufficiency with examples and argue that an ideal situation for ND is to have smaller intra-class ND than inter-class ND. To formulate this idea and have a better understanding of homophily, we propose Contextual Stochastic Block Model for Homophily (CSBM-H) and define two metrics, Probabilistic Bayes Error (PBE) and Expected Negative KL-divergence (ENKL), to quantify ND, through which we can also find how intra- and inter-class ND influence ND together. We visualize the results and give detailed analysis. Through experiments, we verified that the superiority of GNNs is indeed closely related to both intra- and inter-class ND regardless of homophily levels, based on which we define Kernel Performance Metric (KPM). KPM is a new non-linear, feature-based metric, which is tested to be more effective than the existing homophily metrics on revealing the advantage and disadvantage of GNNs on synthetic and real-world datasets.

Complete the Missing Half: Augmenting Aggregation Filtering with Diversification for Graph Convolutional Neural Networks

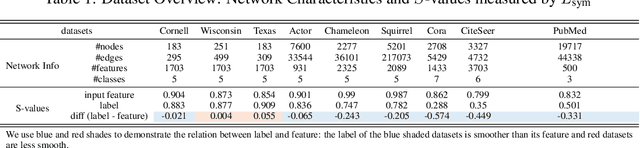
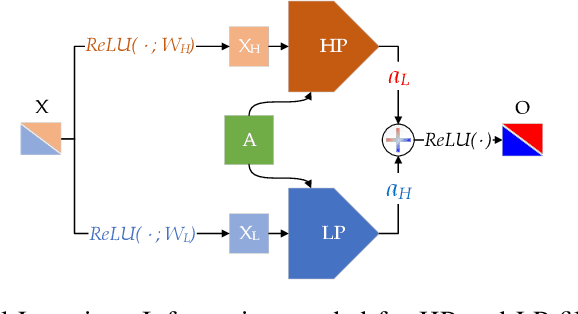
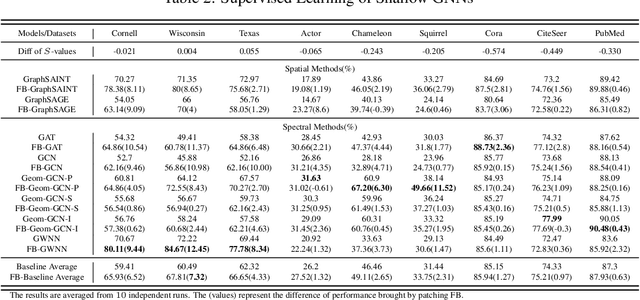
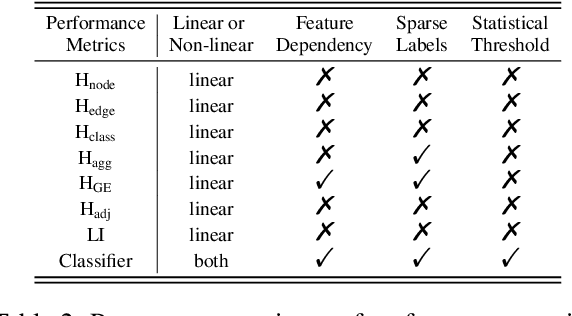
The core operation of current Graph Neural Networks (GNNs) is the aggregation enabled by the graph Laplacian or message passing, which filters the neighborhood information of nodes. Though effective for various tasks, in this paper, we show that they are potentially a problematic factor underlying all GNN models for learning on certain datasets, as they force the node representations similar, making the nodes gradually lose their identity and become indistinguishable. Hence, we augment the aggregation operations with their dual, i.e. diversification operators that make the node more distinct and preserve the identity. Such augmentation replaces the aggregation with a two-channel filtering process that, in theory, is beneficial for enriching the node representations. In practice, the proposed two-channel filters can be easily patched on existing GNN methods with diverse training strategies, including spectral and spatial (message passing) methods. In the experiments, we observe desired characteristics of the models and significant performance boost upon the baselines on 9 node classification tasks.

When Do We Need GNN for Node Classification?

Graph Neural Networks (GNNs) extend basic Neural Networks (NNs) by additionally making use of graph structure based on the relational inductive bias (edge bias), rather than treating the nodes as collections of independent and identically distributed (\iid) samples. Though GNNs are believed to outperform basic NNs in real-world tasks, it is found that in some cases, GNNs have little performance gain or even underperform graph-agnostic NNs. To identify these cases, based on graph signal processing and statistical hypothesis testing, we propose two measures which analyze the cases in which the edge bias in features and labels does not provide advantages. Based on the measures, a threshold value can be given to predict the potential performance advantages of graph-aware models over graph-agnostic models.