Liheng Ma
TrasMuon: Trust-Region Adaptive Scaling for Orthogonalized Momentum Optimizers
Feb 13, 2026Abstract:Muon-style optimizers leverage Newton-Schulz (NS) iterations to orthogonalize updates, yielding update geometries that often outperform Adam-series methods. However, this orthogonalization discards magnitude information, rendering training sensitive to step-size hyperparameters and vulnerable to high-energy bursts. To mitigate this, we introduce TrasMuon (\textbf{T}rust \textbf{R}egion \textbf{A}daptive \textbf{S}caling \textbf{Muon}). TrasMuon preserves the near-isometric geometry of Muon while stabilizing magnitudes through (i) global RMS calibration and (ii) energy-based trust-region clipping. We demonstrate that while reintroducing adaptive scaling improves optimization efficiency, it typically exacerbates instability due to high-energy outliers. TrasMuon addresses this by defining a trust region based on relative energy ratios, confining updates to a stable zone. Empirical experiments on vision and language models demonstrate that TrasMuon converges faster than baselines. Furthermore, experiments without warmup stages confirm TrasMuon's superior stability and robustness.
Enhancing TableQA through Verifiable Reasoning Trace Reward
Jan 30, 2026Abstract:A major challenge in training TableQA agents, compared to standard text- and image-based agents, is that answers cannot be inferred from a static input but must be reasoned through stepwise transformations of the table state, introducing multi-step reasoning complexity and environmental interaction. This leads to a research question: Can explicit feedback on table transformation action improve model reasoning capability? In this work, we introduce RE-Tab, a plug-and-play framework that architecturally enhances trajectory search via lightweight, training-free reward modeling by formulating the problem as a Partially Observable Markov Decision Process. We demonstrate that providing explicit verifiable rewards during State Transition (``What is the best action?'') and Simulative Reasoning (``Am I sure about the output?'') is crucial to steer the agent's navigation in table states. By enforcing stepwise reasoning with reward feedback in table transformations, RE-Tab achieves state-of-the-art performance in TableQA with almost 25\% drop in inference cost. Furthermore, a direct plug-and-play implementation of RE-Tab brings up to 41.77% improvement in QA accuracy and 33.33% drop in test-time inference samples for consistent answer. Consistent improvement pattern across various LLMs and state-of-the-art benchmarks further confirms RE-Tab's generalisability. The repository is available at https://github.com/ThomasK1018/RE_Tab .
Dynamic Quantization Error Propagation in Encoder-Decoder ASR Quantization
Jan 05, 2026Abstract:Running Automatic Speech Recognition (ASR) models on memory-constrained edge devices requires efficient compression. While layer-wise post-training quantization is effective, it suffers from error accumulation, especially in encoder-decoder architectures. Existing solutions like Quantization Error Propagation (QEP) are suboptimal for ASR due to the model's heterogeneity, processing acoustic features in the encoder while generating text in the decoder. To address this, we propose Fine-grained Alpha for Dynamic Quantization Error Propagation (FADE), which adaptively controls the trade-off between cross-layer error correction and local quantization. Experiments show that FADE significantly improves stability by reducing performance variance across runs, while simultaneously surpassing baselines in mean WER.
GraphPPD: Posterior Predictive Modelling for Graph-Level Inference
Aug 23, 2025Abstract:Accurate modelling and quantification of predictive uncertainty is crucial in deep learning since it allows a model to make safer decisions when the data is ambiguous and facilitates the users' understanding of the model's confidence in its predictions. Along with the tremendously increasing research focus on \emph{graph neural networks} (GNNs) in recent years, there have been numerous techniques which strive to capture the uncertainty in their predictions. However, most of these approaches are specifically designed for node or link-level tasks and cannot be directly applied to graph-level learning problems. In this paper, we propose a novel variational modelling framework for the \emph{posterior predictive distribution}~(PPD) to obtain uncertainty-aware prediction in graph-level learning tasks. Based on a graph-level embedding derived from one of the existing GNNs, our framework can learn the PPD in a data-adaptive fashion. Experimental results on several benchmark datasets exhibit the effectiveness of our approach.
An Entity Linking Agent for Question Answering
Aug 05, 2025Abstract:Some Question Answering (QA) systems rely on knowledge bases (KBs) to provide accurate answers. Entity Linking (EL) plays a critical role in linking natural language mentions to KB entries. However, most existing EL methods are designed for long contexts and do not perform well on short, ambiguous user questions in QA tasks. We propose an entity linking agent for QA, based on a Large Language Model that simulates human cognitive workflows. The agent actively identifies entity mentions, retrieves candidate entities, and makes decision. To verify the effectiveness of our agent, we conduct two experiments: tool-based entity linking and QA task evaluation. The results confirm the robustness and effectiveness of our agent.
SKOLR: Structured Koopman Operator Linear RNN for Time-Series Forecasting
Jun 17, 2025Abstract:Koopman operator theory provides a framework for nonlinear dynamical system analysis and time-series forecasting by mapping dynamics to a space of real-valued measurement functions, enabling a linear operator representation. Despite the advantage of linearity, the operator is generally infinite-dimensional. Therefore, the objective is to learn measurement functions that yield a tractable finite-dimensional Koopman operator approximation. In this work, we establish a connection between Koopman operator approximation and linear Recurrent Neural Networks (RNNs), which have recently demonstrated remarkable success in sequence modeling. We show that by considering an extended state consisting of lagged observations, we can establish an equivalence between a structured Koopman operator and linear RNN updates. Building on this connection, we present SKOLR, which integrates a learnable spectral decomposition of the input signal with a multilayer perceptron (MLP) as the measurement functions and implements a structured Koopman operator via a highly parallel linear RNN stack. Numerical experiments on various forecasting benchmarks and dynamical systems show that this streamlined, Koopman-theory-based design delivers exceptional performance.
Reinforcing Question Answering Agents with Minimalist Policy Gradient Optimization
May 20, 2025Abstract:Large Language Models (LLMs) have demonstrated remarkable versatility, due to the lack of factual knowledge, their application to Question Answering (QA) tasks remains hindered by hallucination. While Retrieval-Augmented Generation mitigates these issues by integrating external knowledge, existing approaches rely heavily on in-context learning, whose performance is constrained by the fundamental reasoning capabilities of LLMs. In this paper, we propose Mujica, a Multi-hop Joint Intelligence for Complex Question Answering, comprising a planner that decomposes questions into a directed acyclic graph of subquestions and a worker that resolves questions via retrieval and reasoning. Additionally, we introduce MyGO (Minimalist policy Gradient Optimization), a novel reinforcement learning method that replaces traditional policy gradient updates with Maximum Likelihood Estimation (MLE) by sampling trajectories from an asymptotically optimal policy. MyGO eliminates the need for gradient rescaling and reference models, ensuring stable and efficient training. Empirical results across multiple datasets demonstrate the effectiveness of Mujica-MyGO in enhancing multi-hop QA performance for various LLMs, offering a scalable and resource-efficient solution for complex QA tasks.
Simplifying Graph Transformers
Apr 17, 2025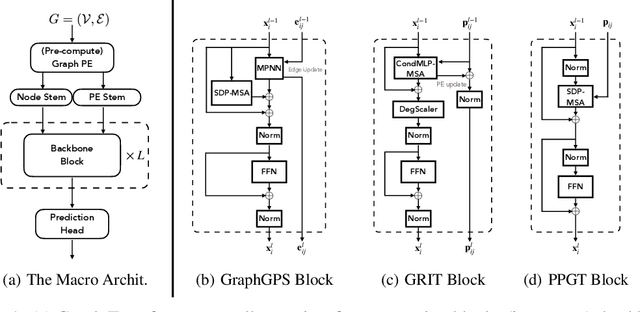
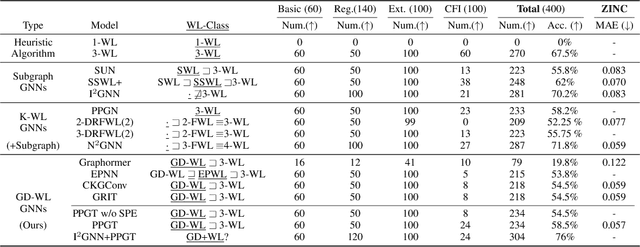
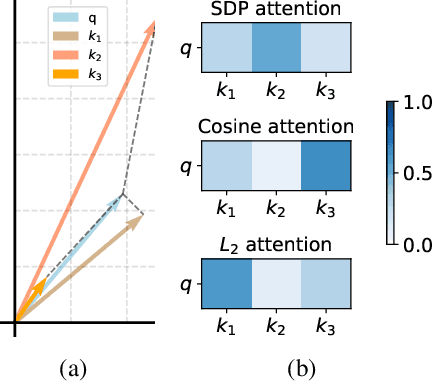
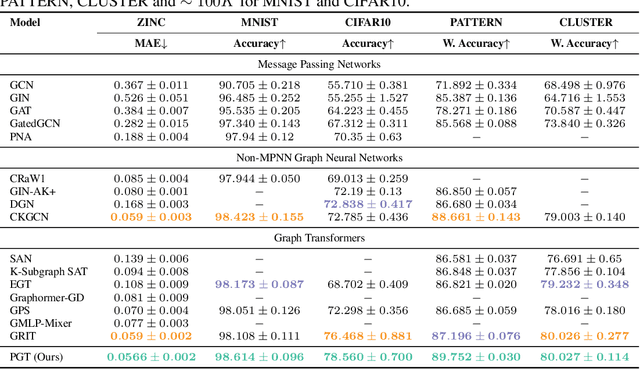
Abstract:Transformers have attained outstanding performance across various modalities, employing scaled-dot-product (SDP) attention mechanisms. Researchers have attempted to migrate Transformers to graph learning, but most advanced Graph Transformers are designed with major architectural differences, either integrating message-passing or incorporating sophisticated attention mechanisms. These complexities prevent the easy adoption of Transformer training advances. We propose three simple modifications to the plain Transformer to render it applicable to graphs without introducing major architectural distortions. Specifically, we advocate for the use of (1) simplified $L_2$ attention to measure the magnitude closeness of tokens; (2) adaptive root-mean-square normalization to preserve token magnitude information; and (3) a relative positional encoding bias with a shared encoder. Significant performance gains across a variety of graph datasets justify the effectiveness of our proposed modifications. Furthermore, empirical evaluation on the expressiveness benchmark reveals noteworthy realized expressiveness in the graph isomorphism.
Sparse Decomposition of Graph Neural Networks
Oct 25, 2024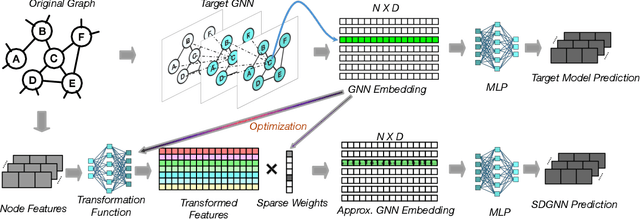
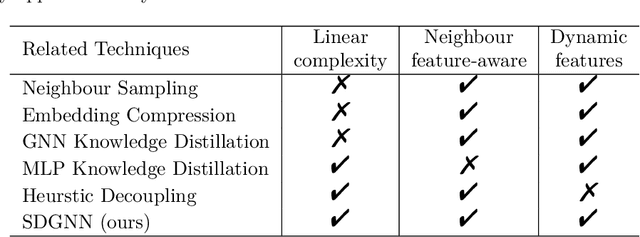
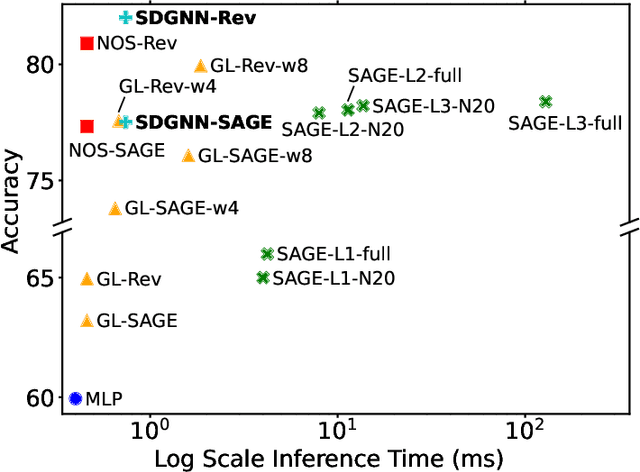

Abstract:Graph Neural Networks (GNN) exhibit superior performance in graph representation learning, but their inference cost can be high, due to an aggregation operation that can require a memory fetch for a very large number of nodes. This inference cost is the major obstacle to deploying GNN models with \emph{online prediction} to reflect the potentially dynamic node features. To address this, we propose an approach to reduce the number of nodes that are included during aggregation. We achieve this through a sparse decomposition, learning to approximate node representations using a weighted sum of linearly transformed features of a carefully selected subset of nodes within the extended neighbourhood. The approach achieves linear complexity with respect to the average node degree and the number of layers in the graph neural network. We introduce an algorithm to compute the optimal parameters for the sparse decomposition, ensuring an accurate approximation of the original GNN model, and present effective strategies to reduce the training time and improve the learning process. We demonstrate via extensive experiments that our method outperforms other baselines designed for inference speedup, achieving significant accuracy gains with comparable inference times for both node classification and spatio-temporal forecasting tasks.
The Heterophilic Graph Learning Handbook: Benchmarks, Models, Theoretical Analysis, Applications and Challenges
Jul 12, 2024



Abstract:Homophily principle, \ie{} nodes with the same labels or similar attributes are more likely to be connected, has been commonly believed to be the main reason for the superiority of Graph Neural Networks (GNNs) over traditional Neural Networks (NNs) on graph-structured data, especially on node-level tasks. However, recent work has identified a non-trivial set of datasets where GNN's performance compared to the NN's is not satisfactory. Heterophily, i.e. low homophily, has been considered the main cause of this empirical observation. People have begun to revisit and re-evaluate most existing graph models, including graph transformer and its variants, in the heterophily scenario across various kinds of graphs, e.g. heterogeneous graphs, temporal graphs and hypergraphs. Moreover, numerous graph-related applications are found to be closely related to the heterophily problem. In the past few years, considerable effort has been devoted to studying and addressing the heterophily issue. In this survey, we provide a comprehensive review of the latest progress on heterophilic graph learning, including an extensive summary of benchmark datasets and evaluation of homophily metrics on synthetic graphs, meticulous classification of the most updated supervised and unsupervised learning methods, thorough digestion of the theoretical analysis on homophily/heterophily, and broad exploration of the heterophily-related applications. Notably, through detailed experiments, we are the first to categorize benchmark heterophilic datasets into three sub-categories: malignant, benign and ambiguous heterophily. Malignant and ambiguous datasets are identified as the real challenging datasets to test the effectiveness of new models on the heterophily challenge. Finally, we propose several challenges and future directions for heterophilic graph representation learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge