Complete the Missing Half: Augmenting Aggregation Filtering with Diversification for Graph Convolutional Neural Networks
Paper and Code
Dec 21, 2022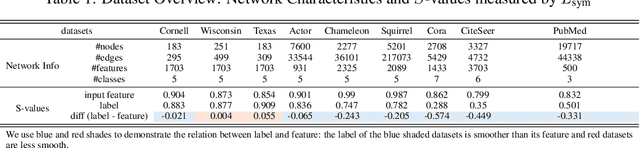
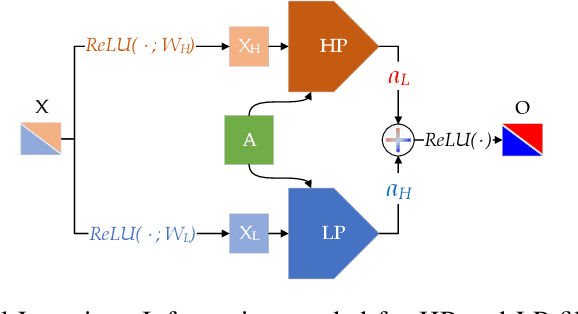

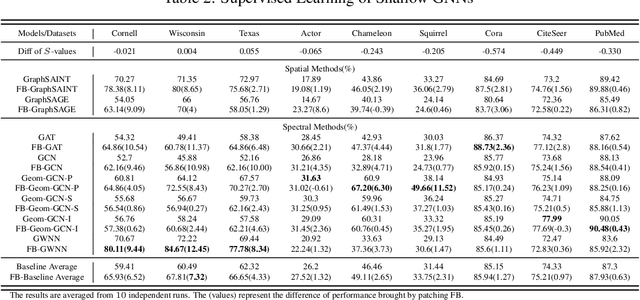
The core operation of current Graph Neural Networks (GNNs) is the aggregation enabled by the graph Laplacian or message passing, which filters the neighborhood information of nodes. Though effective for various tasks, in this paper, we show that they are potentially a problematic factor underlying all GNN models for learning on certain datasets, as they force the node representations similar, making the nodes gradually lose their identity and become indistinguishable. Hence, we augment the aggregation operations with their dual, i.e. diversification operators that make the node more distinct and preserve the identity. Such augmentation replaces the aggregation with a two-channel filtering process that, in theory, is beneficial for enriching the node representations. In practice, the proposed two-channel filters can be easily patched on existing GNN methods with diverse training strategies, including spectral and spatial (message passing) methods. In the experiments, we observe desired characteristics of the models and significant performance boost upon the baselines on 9 node classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge