Vahid Partovi Nia
Huawei Noah's Ark Lab
Enterprise Resource Planning Using Multi-type Transformers in Ferro-Titanium Industry
Jan 28, 2026Abstract:Combinatorial optimization problems such as the Job-Shop Scheduling Problem (JSP) and Knapsack Problem (KP) are fundamental challenges in operations research, logistics, and eterprise resource planning (ERP). These problems often require sophisticated algorithms to achieve near-optimal solutions within practical time constraints. Recent advances in deep learning have introduced transformer-based architectures as promising alternatives to traditional heuristics and metaheuristics. We leverage the Multi-Type Transformer (MTT) architecture to address these benchmarks in a unified framework. We present an extensive experimental evaluation across standard benchmark datasets for JSP and KP, demonstrating that MTT achieves competitive performance on different size of these benchmark problems. We showcase the potential of multi-type attention on a real application in Ferro-Titanium industry. To the best of our knowledge, we are the first to apply multi-type transformers in real manufacturing.
Tiny Noise-Robust Voice Activity Detector for Voice Assistants
Jul 29, 2025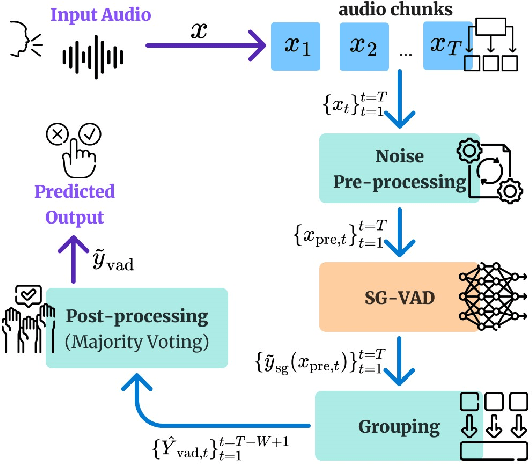
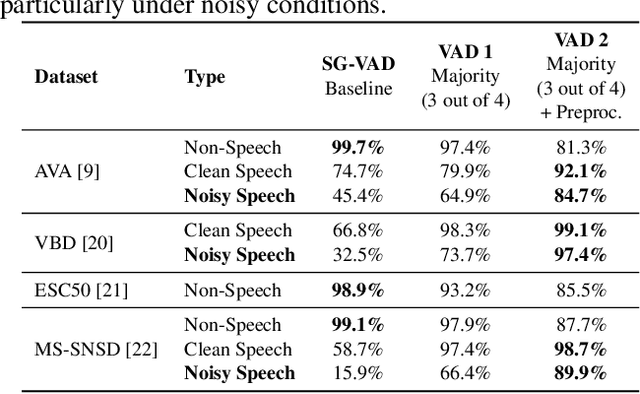
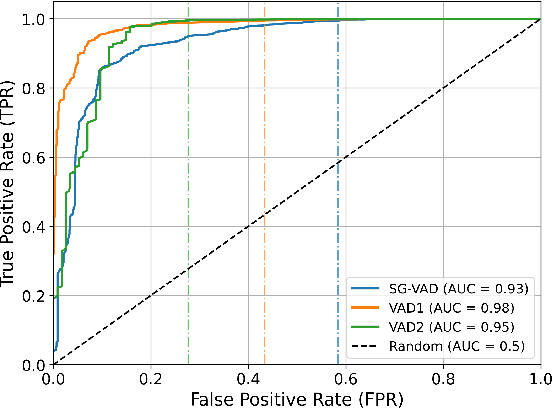
Abstract:Voice Activity Detection (VAD) in the presence of background noise remains a challenging problem in speech processing. Accurate VAD is essential in automatic speech recognition, voice-to-text, conversational agents, etc, where noise can severely degrade the performance. A modern application includes the voice assistant, specially mounted on Artificial Intelligence of Things (AIoT) devices such as cell phones, smart glasses, earbuds, etc, where the voice signal includes background noise. Therefore, VAD modules must remain light-weight due to their practical on-device limitation. The existing models often struggle with low signal-to-noise ratios across diverse acoustic environments. A simple VAD often detects human voice in a clean environment, but struggles to detect the human voice in noisy conditions. We propose a noise-robust VAD that comprises a light-weight VAD, with data pre-processing and post-processing added modules to handle the background noise. This approach significantly enhances the VAD accuracy in noisy environments and requires neither a larger model, nor fine-tuning. Experimental results demonstrate that our approach achieves a notable improvement compared to baselines, particularly in environments with high background noise interference. This modified VAD additionally improving clean speech detection.
* Hamed Jafarzadeh Asl and Mahsa Ghazvini Nejad contributed equally to this work
PoTPTQ: A Two-step Power-of-Two Post-training for LLMs
Jul 16, 2025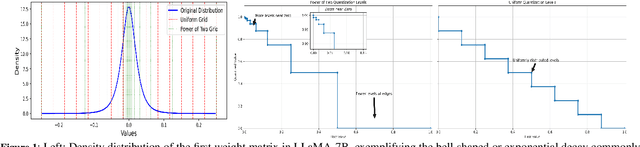
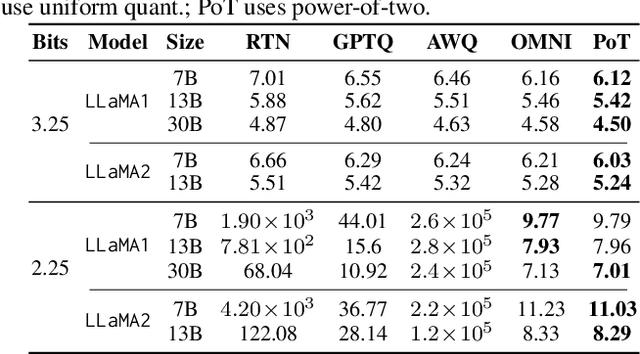
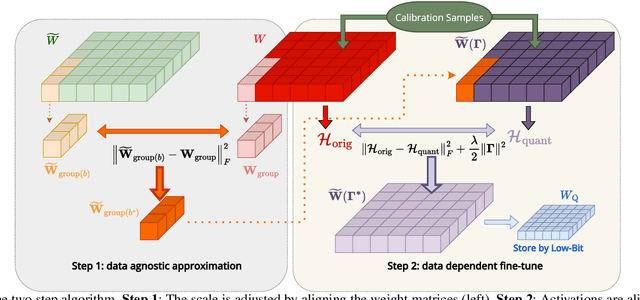
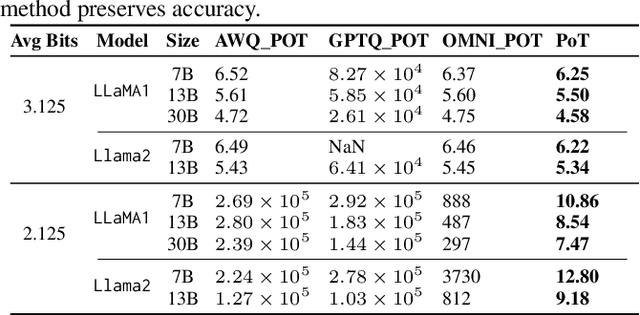
Abstract:Large Language Models (LLMs) have demonstrated remarkable performance across various natural language processing (NLP) tasks. However, their deployment is challenging due to the substantial computational resources required. Power-of-two (PoT) quantization is a general tool to counteract this difficulty. Albeit previous works on PoT quantization can be efficiently dequantized on CPUs using fixed-point addition, it showed less effectiveness on GPUs. The reason is entanglement of the sign bit and sequential bit manipulations needed for dequantization. We propose a novel POT quantization framework for LLM weights that (i) outperforms state-of-the-art accuracy in extremely low-precision number formats, and (ii) enables faster inference through more efficient dequantization. To maintain the accuracy of the quantized model, we introduce a two-step post-training algorithm: (i) initialize the quantization scales with a robust starting point, and (ii) refine these scales using a minimal calibration set. The performance of our PoT post-training algorithm surpasses the current state-of-the-art in integer quantization, particularly at low precisions such as 2- and 3-bit formats. Our PoT quantization accelerates the dequantization step required for the floating point inference and leads to $3.67\times$ speed up on a NVIDIA V100, and $1.63\times$ on a NVIDIA RTX 4090, compared to uniform integer dequantization.
Rethinking Post-Training Quantization: Introducing a Statistical Pre-Calibration Approach
Jan 15, 2025



Abstract:As Large Language Models (LLMs) become increasingly computationally complex, developing efficient deployment strategies, such as quantization, becomes crucial. State-of-the-art Post-training Quantization (PTQ) techniques often rely on calibration processes to maintain the accuracy of these models. However, while these calibration techniques can enhance performance in certain domains, they may not be as effective in others. This paper aims to draw attention to robust statistical approaches that can mitigate such issues. We propose a weight-adaptive PTQ method that can be considered a precursor to calibration-based PTQ methods, guiding the quantization process to preserve the distribution of weights by minimizing the Kullback-Leibler divergence between the quantized weights and the originally trained weights. This minimization ensures that the quantized model retains the Shannon information content of the original model to a great extent, guaranteeing robust and efficient deployment across many tasks. As such, our proposed approach can perform on par with most common calibration-based PTQ methods, establishing a new pre-calibration step for further adjusting the quantized weights with calibration. We show that our pre-calibration results achieve the same accuracy as some existing calibration-based PTQ methods on various LLMs.
OAC: Output-adaptive Calibration for Accurate Post-training Quantization
May 23, 2024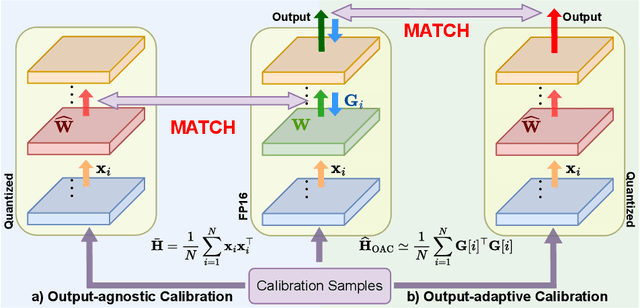
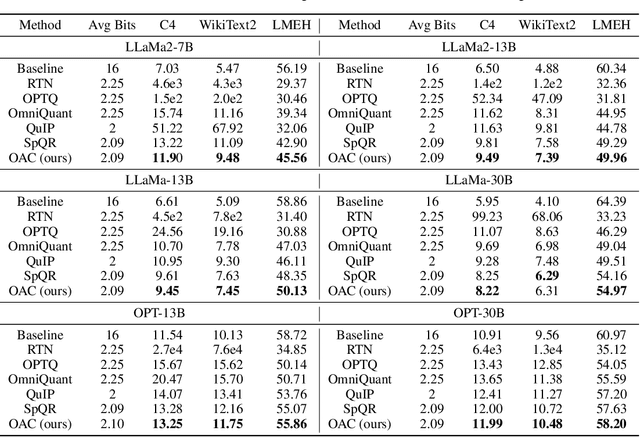
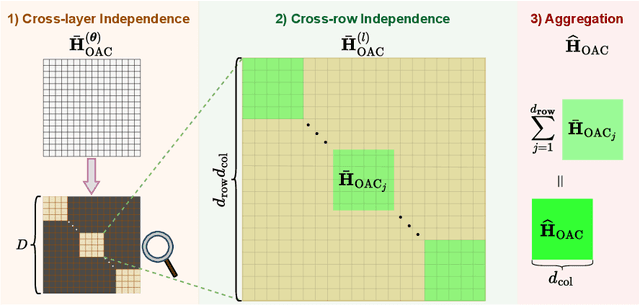
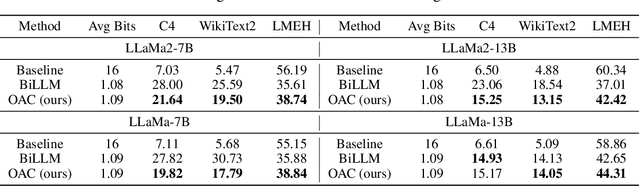
Abstract:Deployment of Large Language Models (LLMs) has major computational costs, due to their rapidly expanding size. Compression of LLMs reduces the memory footprint, latency, and energy required for their inference. Post-training Quantization (PTQ) techniques have been developed to compress LLMs while avoiding expensive re-training. Most PTQ approaches formulate the quantization error based on a layer-wise $\ell_2$ loss, ignoring the model output. Then, each layer is calibrated using its layer-wise Hessian to update the weights towards minimizing the $\ell_2$ quantization error. The Hessian is also used for detecting the most salient weights to quantization. Such PTQ approaches are prone to accuracy drop in low-precision quantization. We propose Output-adaptive Calibration (OAC) to incorporate the model output in the calibration process. We formulate the quantization error based on the distortion of the output cross-entropy loss. OAC approximates the output-adaptive Hessian for each layer under reasonable assumptions to reduce the computational complexity. The output-adaptive Hessians are used to update the weight matrices and detect the salient weights towards maintaining the model output. Our proposed method outperforms the state-of-the-art baselines such as SpQR and BiLLM, especially, at extreme low-precision (2-bit and binary) quantization.
AdpQ: A Zero-shot Calibration Free Adaptive Post Training Quantization Method for LLMs
May 22, 2024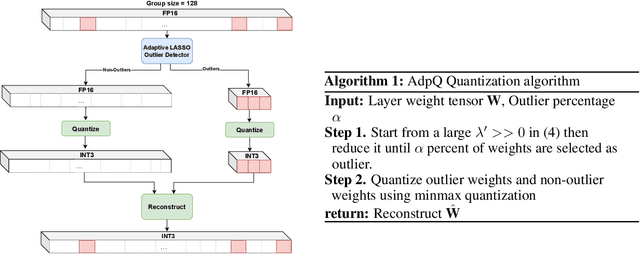

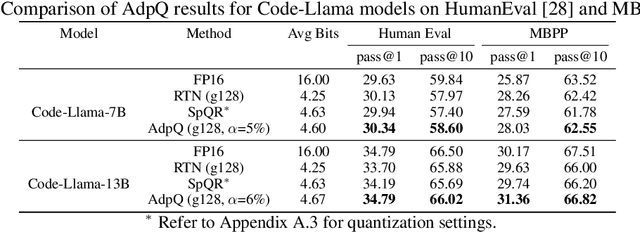
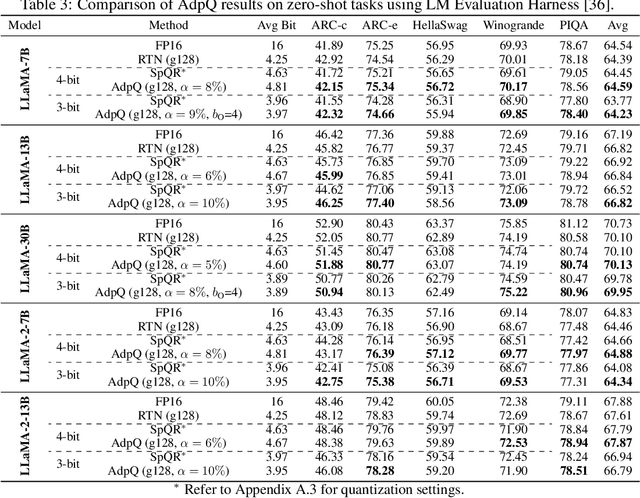
Abstract:The ever-growing computational complexity of Large Language Models (LLMs) necessitates efficient deployment strategies. The current state-of-the-art approaches for Post-training Quantization (PTQ) often require calibration to achieve the desired accuracy. This paper presents AdpQ, a novel zero-shot adaptive PTQ method for LLMs that achieves the state-of-the-art performance in low-precision quantization (e.g. 3-bit) without requiring any calibration data. Inspired by Adaptive LASSO regression model, our proposed approach tackles the challenge of outlier activations by separating salient weights using an adaptive soft-thresholding method. Guided by Adaptive LASSO, this method ensures that the quantized weights distribution closely follows the originally trained weights and eliminates the need for calibration data entirely, setting our method apart from popular approaches such as SpQR and AWQ. Furthermore, our method offers an additional benefit in terms of privacy preservation by eliminating any calibration or training data. We also delve deeper into the information-theoretic underpinnings of the proposed method. We demonstrate that it leverages the Adaptive LASSO to minimize the Kullback-Leibler divergence between the quantized weights and the originally trained weights. This minimization ensures the quantized model retains the Shannon information content of the original model to a great extent, guaranteeing efficient deployment without sacrificing accuracy or information. Our results achieve the same accuracy as the existing methods on various LLM benchmarks while the quantization time is reduced by at least 10x, solidifying our contribution to efficient and privacy-preserving LLM deployment.
Understanding Neural Network Binarization with Forward and Backward Proximal Quantizers
Feb 27, 2024Abstract:In neural network binarization, BinaryConnect (BC) and its variants are considered the standard. These methods apply the sign function in their forward pass and their respective gradients are backpropagated to update the weights. However, the derivative of the sign function is zero whenever defined, which consequently freezes training. Therefore, implementations of BC (e.g., BNN) usually replace the derivative of sign in the backward computation with identity or other approximate gradient alternatives. Although such practice works well empirically, it is largely a heuristic or ''training trick.'' We aim at shedding some light on these training tricks from the optimization perspective. Building from existing theory on ProxConnect (PC, a generalization of BC), we (1) equip PC with different forward-backward quantizers and obtain ProxConnect++ (PC++) that includes existing binarization techniques as special cases; (2) derive a principled way to synthesize forward-backward quantizers with automatic theoretical guarantees; (3) illustrate our theory by proposing an enhanced binarization algorithm BNN++; (4) conduct image classification experiments on CNNs and vision transformers, and empirically verify that BNN++ generally achieves competitive results on binarizing these models.
Mitigating Outlier Activations in Low-Precision Fine-Tuning of Language Models
Dec 15, 2023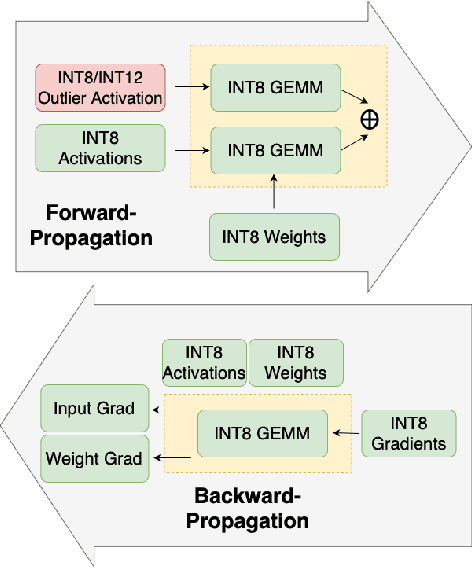

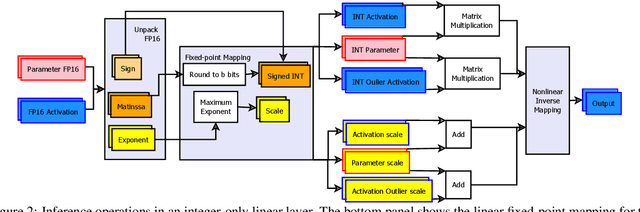
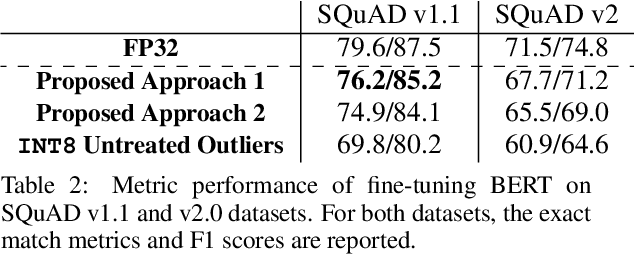
Abstract:Low-precision fine-tuning of language models has gained prominence as a cost-effective and energy-efficient approach to deploying large-scale models in various applications. However, this approach is susceptible to the existence of outlier values in activation. The outlier values in the activation can negatively affect the performance of fine-tuning language models in the low-precision regime since they affect the scaling factor and thus make representing smaller values harder. This paper investigates techniques for mitigating outlier activation in low-precision integer fine-tuning of the language models. Our proposed novel approach enables us to represent the outlier activation values in 8-bit integers instead of floating-point (FP16) values. The benefit of using integers for outlier values is that it enables us to use operator tiling to avoid performing 16-bit integer matrix multiplication to address this problem effectively. We provide theoretical analysis and supporting experiments to demonstrate the effectiveness of our approach in improving the robustness and performance of low-precision fine-tuned language models.
Mathematical Challenges in Deep Learning
Mar 24, 2023



Abstract:Deep models are dominating the artificial intelligence (AI) industry since the ImageNet challenge in 2012. The size of deep models is increasing ever since, which brings new challenges to this field with applications in cell phones, personal computers, autonomous cars, and wireless base stations. Here we list a set of problems, ranging from training, inference, generalization bound, and optimization with some formalism to communicate these challenges with mathematicians, statisticians, and theoretical computer scientists. This is a subjective view of the research questions in deep learning that benefits the tech industry in long run.
Scaling Deep Networks with the Mesh Adaptive Direct Search algorithm
Jan 17, 2023Abstract:Deep neural networks are getting larger. Their implementation on edge and IoT devices becomes more challenging and moved the community to design lighter versions with similar performance. Standard automatic design tools such as \emph{reinforcement learning} and \emph{evolutionary computing} fundamentally rely on cheap evaluations of an objective function. In the neural network design context, this objective is the accuracy after training, which is expensive and time-consuming to evaluate. We automate the design of a light deep neural network for image classification using the \emph{Mesh Adaptive Direct Search}(MADS) algorithm, a mature derivative-free optimization method that effectively accounts for the expensive blackbox nature of the objective function to explore the design space, even in the presence of constraints.Our tests show competitive compression rates with reduced numbers of trials.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge