Non-Asymptotic Analysis of Online Local Private Learning with SGD

Differentially Private Stochastic Gradient Descent (DP-SGD) has been widely used for solving optimization problems with privacy guarantees in machine learning and statistics. Despite this, a systematic non-asymptotic convergence analysis for DP-SGD, particularly in the context of online problems and local differential privacy (LDP) models, remains largely elusive. Existing non-asymptotic analyses have focused on non-private optimization methods, and hence are not applicable to privacy-preserving optimization problems. This work initiates the analysis to bridge this gap and opens the door to non-asymptotic convergence analysis of private optimization problems. A general framework is investigated for the online LDP model in stochastic optimization problems. We assume that sensitive information from individuals is collected sequentially and aim to estimate, in real-time, a static parameter that pertains to the population of interest. Most importantly, we conduct a comprehensive non-asymptotic convergence analysis of the proposed estimators in finite-sample situations, which gives their users practical guidelines regarding the effect of various hyperparameters, such as step size, parameter dimensions, and privacy budgets, on convergence rates. Our proposed estimators are validated in the theoretical and practical realms by rigorous mathematical derivations and carefully constructed numerical experiments.

Deep Fair Learning: A Unified Framework for Fine-tuning Representations with Sufficient Networks

Ensuring fairness in machine learning is a critical and challenging task, as biased data representations often lead to unfair predictions. To address this, we propose Deep Fair Learning, a framework that integrates nonlinear sufficient dimension reduction with deep learning to construct fair and informative representations. By introducing a novel penalty term during fine-tuning, our method enforces conditional independence between sensitive attributes and learned representations, addressing bias at its source while preserving predictive performance. Unlike prior methods, it supports diverse sensitive attributes, including continuous, discrete, binary, or multi-group types. Experiments on various types of data structure show that our approach achieves a superior balance between fairness and utility, significantly outperforming state-of-the-art baselines.

Online federated learning framework for classification

In this paper, we develop a novel online federated learning framework for classification, designed to handle streaming data from multiple clients while ensuring data privacy and computational efficiency. Our method leverages the generalized distance-weighted discriminant technique, making it robust to both homogeneous and heterogeneous data distributions across clients. In particular, we develop a new optimization algorithm based on the Majorization-Minimization principle, integrated with a renewable estimation procedure, enabling efficient model updates without full retraining. We provide a theoretical guarantee for the convergence of our estimator, proving its consistency and asymptotic normality under standard regularity conditions. In addition, we establish that our method achieves Bayesian risk consistency, ensuring its reliability for classification tasks in federated environments. We further incorporate differential privacy mechanisms to enhance data security, protecting client information while maintaining model performance. Extensive numerical experiments on both simulated and real-world datasets demonstrate that our approach delivers high classification accuracy, significant computational efficiency gains, and substantial savings in data storage requirements compared to existing methods.

A Deep Bayesian Nonparametric Framework for Robust Mutual Information Estimation

Mutual Information (MI) is a crucial measure for capturing dependencies between variables, but exact computation is challenging in high dimensions with intractable likelihoods, impacting accuracy and robustness. One idea is to use an auxiliary neural network to train an MI estimator; however, methods based on the empirical distribution function (EDF) can introduce sharp fluctuations in the MI loss due to poor out-of-sample performance, destabilizing convergence. We present a Bayesian nonparametric (BNP) solution for training an MI estimator by constructing the MI loss with a finite representation of the Dirichlet process posterior to incorporate regularization in the training process. With this regularization, the MI loss integrates both prior knowledge and empirical data to reduce the loss sensitivity to fluctuations and outliers in the sample data, especially in small sample settings like mini-batches. This approach addresses the challenge of balancing accuracy and low variance by effectively reducing variance, leading to stabilized and robust MI loss gradients during training and enhancing the convergence of the MI approximation while offering stronger theoretical guarantees for convergence. We explore the application of our estimator in maximizing MI between the data space and the latent space of a variational autoencoder. Experimental results demonstrate significant improvements in convergence over EDF-based methods, with applications across synthetic and real datasets, notably in 3D CT image generation, yielding enhanced structure discovery and reduced overfitting in data synthesis. While this paper focuses on generative models in application, the proposed estimator is not restricted to this setting and can be applied more broadly in various BNP learning procedures.

A Consensus Privacy Metrics Framework for Synthetic Data

Synthetic data generation is one approach for sharing individual-level data. However, to meet legislative requirements, it is necessary to demonstrate that the individuals' privacy is adequately protected. There is no consolidated standard for measuring privacy in synthetic data. Through an expert panel and consensus process, we developed a framework for evaluating privacy in synthetic data. Our findings indicate that current similarity metrics fail to measure identity disclosure, and their use is discouraged. For differentially private synthetic data, a privacy budget other than close to zero was not considered interpretable. There was consensus on the importance of membership and attribute disclosure, both of which involve inferring personal information about an individual without necessarily revealing their identity. The resultant framework provides precise recommendations for metrics that address these types of disclosures effectively. Our findings further present specific opportunities for future research that can help with widespread adoption of synthetic data.

Statistical Undersampling with Mutual Information and Support Points

Class imbalance and distributional differences in large datasets present significant challenges for classification tasks machine learning, often leading to biased models and poor predictive performance for minority classes. This work introduces two novel undersampling approaches: mutual information-based stratified simple random sampling and support points optimization. These methods prioritize representative data selection, effectively minimizing information loss. Empirical results across multiple classification tasks demonstrate that our methods outperform traditional undersampling techniques, achieving higher balanced classification accuracy. These findings highlight the potential of combining statistical concepts with machine learning to address class imbalance in practical applications.

FedSTaS: Client Stratification and Client Level Sampling for Efficient Federated Learning

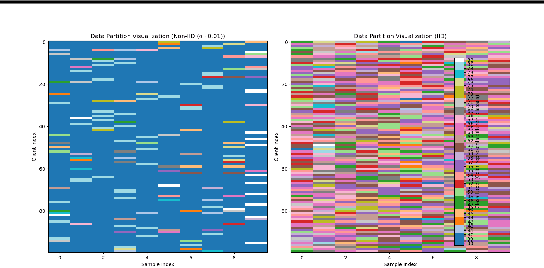
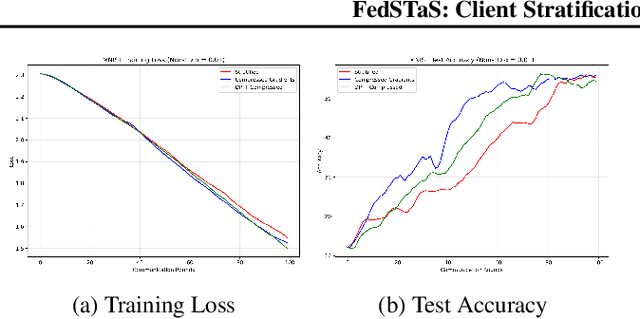
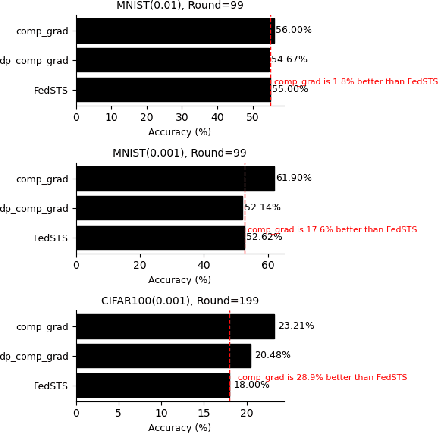
Federated learning (FL) is a machine learning methodology that involves the collaborative training of a global model across multiple decentralized clients in a privacy-preserving way. Several FL methods are introduced to tackle communication inefficiencies but do not address how to sample participating clients in each round effectively and in a privacy-preserving manner. In this paper, we propose \textit{FedSTaS}, a client and data-level sampling method inspired by \textit{FedSTS} and \textit{FedSampling}. In each federated learning round, \textit{FedSTaS} stratifies clients based on their compressed gradients, re-allocate the number of clients to sample using an optimal Neyman allocation, and sample local data from each participating clients using a data uniform sampling strategy. Experiments on three datasets show that \textit{FedSTaS} can achieve higher accuracy scores than those of \textit{FedSTS} within a fixed number of training rounds.

Predicting Bitcoin Market Trends with Enhanced Technical Indicator Integration and Classification Models

Thanks to the high potential for profit, trading has become increasingly attractive to investors as the cryptocurrency and stock markets rapidly expand. However, because financial markets are intricate and dynamic, accurately predicting prices remains a significant challenge. The volatile nature of the cryptocurrency market makes it even harder for traders and investors to make decisions. This study presents a machine learning model based on classification to forecast the direction of the cryptocurrency market, i.e., whether prices will increase or decrease. The model is trained using historical data and important technical indicators such as the Moving Average Convergence Divergence, the Relative Strength Index, and Bollinger Bands. We illustrate our approach with an empirical study of the closing price of Bitcoin. Several simulations, including a confusion matrix and Receiver Operating Characteristic curve, are used to assess the model's performance, and the results show a buy/sell signal accuracy of over 92%. These findings demonstrate how machine learning models can assist investors and traders of cryptocurrencies in making wise/informed decisions in a very volatile market.

Evaluation of OpenAI o1: Opportunities and Challenges of AGI

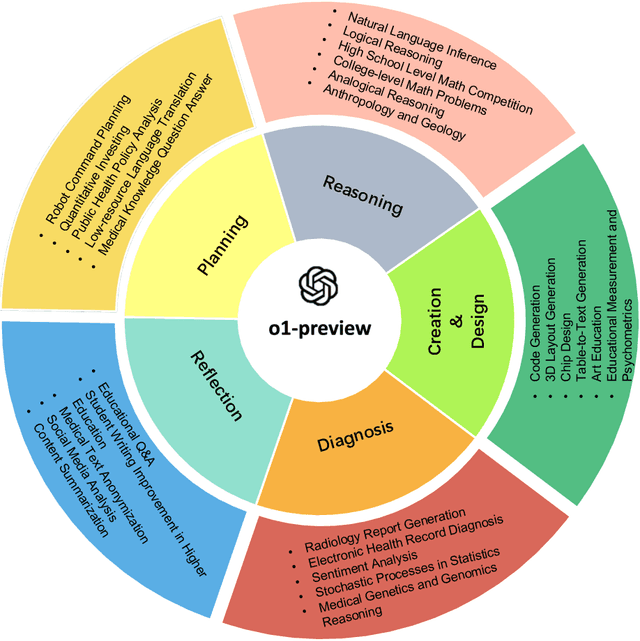
This comprehensive study evaluates the performance of OpenAI's o1-preview large language model across a diverse array of complex reasoning tasks, spanning multiple domains, including computer science, mathematics, natural sciences, medicine, linguistics, and social sciences. Through rigorous testing, o1-preview demonstrated remarkable capabilities, often achieving human-level or superior performance in areas ranging from coding challenges to scientific reasoning and from language processing to creative problem-solving. Key findings include: -83.3% success rate in solving complex competitive programming problems, surpassing many human experts. -Superior ability in generating coherent and accurate radiology reports, outperforming other evaluated models. -100% accuracy in high school-level mathematical reasoning tasks, providing detailed step-by-step solutions. -Advanced natural language inference capabilities across general and specialized domains like medicine. -Impressive performance in chip design tasks, outperforming specialized models in areas such as EDA script generation and bug analysis. -Remarkable proficiency in anthropology and geology, demonstrating deep understanding and reasoning in these specialized fields. -Strong capabilities in quantitative investing. O1 has comprehensive financial knowledge and statistical modeling skills. -Effective performance in social media analysis, including sentiment analysis and emotion recognition. The model excelled particularly in tasks requiring intricate reasoning and knowledge integration across various fields. While some limitations were observed, including occasional errors on simpler problems and challenges with certain highly specialized concepts, the overall results indicate significant progress towards artificial general intelligence.

Oblivious subspace embeddings for compressed Tucker decompositions

Emphasis in the tensor literature on random embeddings (tools for low-distortion dimension reduction) for the canonical polyadic (CP) tensor decomposition has left analogous results for the more expressive Tucker decomposition comparatively lacking. This work establishes general Johnson-Lindenstrauss (JL) type guarantees for the estimation of Tucker decompositions when an oblivious random embedding is applied along each mode. When these embeddings are drawn from a JL-optimal family, the decomposition can be estimated within $\varepsilon$ relative error under restrictions on the embedding dimension that are in line with recent CP results. We implement a higher-order orthogonal iteration (HOOI) decomposition algorithm with random embeddings to demonstrate the practical benefits of this approach and its potential to improve the accessibility of otherwise prohibitive tensor analyses. On moderately large face image and fMRI neuroimaging datasets, empirical results show that substantial dimension reduction is possible with minimal increase in reconstruction error relative to traditional HOOI ($\leq$5% larger error, 50%-60% lower computation time for large models with 50% dimension reduction along each mode). Especially for large tensors, our method outperforms traditional higher-order singular value decomposition (HOSVD) and recently proposed TensorSketch methods.