Shizhe Liang
Unveiling the Mathematical Reasoning in DeepSeek Models: A Comparative Study of Large Language Models
Mar 13, 2025



Abstract:With the rapid evolution of Artificial Intelligence (AI), Large Language Models (LLMs) have reshaped the frontiers of various fields, spanning healthcare, public health, engineering, science, agriculture, education, arts, humanities, and mathematical reasoning. Among these advancements, DeepSeek models have emerged as noteworthy contenders, demonstrating promising capabilities that set them apart from their peers. While previous studies have conducted comparative analyses of LLMs, few have delivered a comprehensive evaluation of mathematical reasoning across a broad spectrum of LLMs. In this work, we aim to bridge this gap by conducting an in-depth comparative study, focusing on the strengths and limitations of DeepSeek models in relation to their leading counterparts. In particular, our study systematically evaluates the mathematical reasoning performance of two DeepSeek models alongside five prominent LLMs across three independent benchmark datasets. The findings reveal several key insights: 1). DeepSeek-R1 consistently achieved the highest accuracy on two of the three datasets, demonstrating strong mathematical reasoning capabilities. 2). The distilled variant of LLMs significantly underperformed compared to its peers, highlighting potential drawbacks in using distillation techniques. 3). In terms of response time, Gemini 2.0 Flash demonstrated the fastest processing speed, outperforming other models in efficiency, which is a crucial factor for real-time applications. Beyond these quantitative assessments, we delve into how architecture, training, and optimization impact LLMs' mathematical reasoning. Moreover, our study goes beyond mere performance comparison by identifying key areas for future advancements in LLM-driven mathematical reasoning. This research enhances our understanding of LLMs' mathematical reasoning and lays the groundwork for future advancements
Large Language Models for Bioinformatics
Jan 10, 2025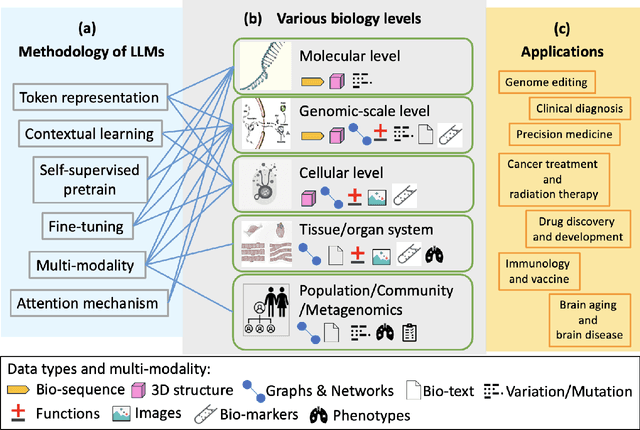
Abstract:With the rapid advancements in large language model (LLM) technology and the emergence of bioinformatics-specific language models (BioLMs), there is a growing need for a comprehensive analysis of the current landscape, computational characteristics, and diverse applications. This survey aims to address this need by providing a thorough review of BioLMs, focusing on their evolution, classification, and distinguishing features, alongside a detailed examination of training methodologies, datasets, and evaluation frameworks. We explore the wide-ranging applications of BioLMs in critical areas such as disease diagnosis, drug discovery, and vaccine development, highlighting their impact and transformative potential in bioinformatics. We identify key challenges and limitations inherent in BioLMs, including data privacy and security concerns, interpretability issues, biases in training data and model outputs, and domain adaptation complexities. Finally, we highlight emerging trends and future directions, offering valuable insights to guide researchers and clinicians toward advancing BioLMs for increasingly sophisticated biological and clinical applications.
Mathematics and Machine Creativity: A Survey on Bridging Mathematics with AI
Dec 21, 2024
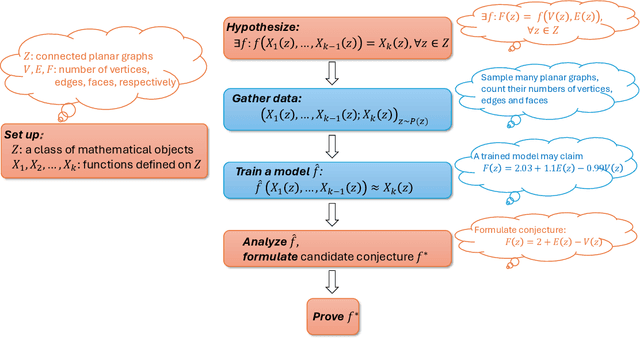
Abstract:This paper presents a comprehensive survey on the applications of artificial intelligence (AI) in mathematical research, highlighting the transformative role AI has begun to play in this domain. Traditionally, AI advancements have heavily relied on theoretical foundations from fields like mathematics and statistics. However, recent developments in AI, particularly in reinforcement learning (RL) and large language models (LLMs), have demonstrated the potential for AI to contribute back to mathematics, offering flexible algorithmic frameworks and powerful inductive reasoning capabilities that support various aspects of mathematical research. This survey aims to establish a bridge between AI and mathematics, providing insights into the mutual benefits and fostering deeper interdisciplinary understanding. In particular, we argue that while current AI and LLMs may struggle with complex deductive reasoning, their inherent creativity holds significant potential to support and inspire mathematical research. This creative capability, often overlooked, could be the key to unlocking new perspectives and methodologies in mathematics. Furthermore, we address the lack of cross-disciplinary communication: mathematicians may not fully comprehend the latest advances in AI, while AI researchers frequently prioritize benchmarks and standardized testing over AI's applications in frontier mathematical research. This paper seeks to close that gap, offering a detailed exploration of AI's basic knowledge, its strengths, and its emerging applications in the mathematical sciences.
HELENE: Hessian Layer-wise Clipping and Gradient Annealing for Accelerating Fine-tuning LLM with Zeroth-order Optimization
Nov 16, 2024



Abstract:Fine-tuning large language models (LLMs) poses significant memory challenges, as the back-propagation process demands extensive resources, especially with growing model sizes. Recent work, MeZO, addresses this issue using a zeroth-order (ZO) optimization method, which reduces memory consumption by matching the usage to the inference phase. However, MeZO experiences slow convergence due to varying curvatures across model parameters. To overcome this limitation, we introduce HELENE, a novel scalable and memory-efficient optimizer that integrates annealed A-GNB gradients with a diagonal Hessian estimation and layer-wise clipping, serving as a second-order pre-conditioner. This combination allows for faster and more stable convergence. Our theoretical analysis demonstrates that HELENE improves convergence rates, particularly for models with heterogeneous layer dimensions, by reducing the dependency on the total parameter space dimension. Instead, the method scales with the largest layer dimension, making it highly suitable for modern LLM architectures. Experimental results on RoBERTa-large and OPT-1.3B across multiple tasks show that HELENE achieves up to a 20x speedup compared to MeZO, with average accuracy improvements of 1.5%. Furthermore, HELENE remains compatible with both full parameter tuning and parameter-efficient fine-tuning (PEFT), outperforming several state-of-the-art optimizers. The codes will be released after reviewing.
Evaluation of OpenAI o1: Opportunities and Challenges of AGI
Sep 27, 2024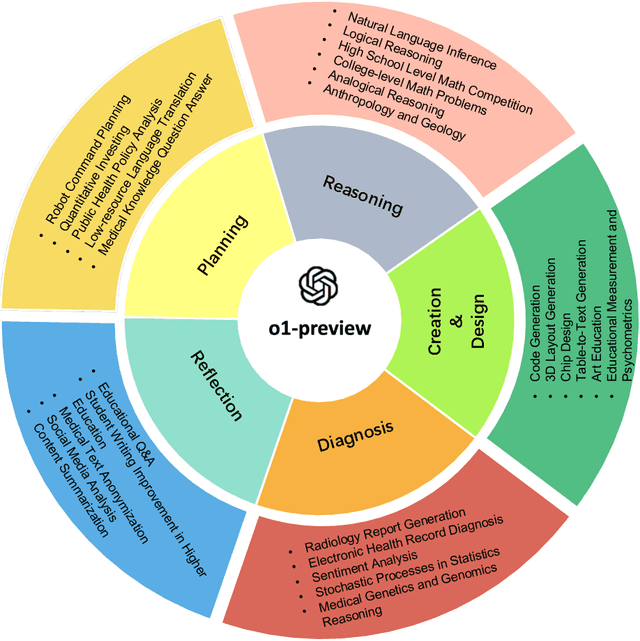


Abstract:This comprehensive study evaluates the performance of OpenAI's o1-preview large language model across a diverse array of complex reasoning tasks, spanning multiple domains, including computer science, mathematics, natural sciences, medicine, linguistics, and social sciences. Through rigorous testing, o1-preview demonstrated remarkable capabilities, often achieving human-level or superior performance in areas ranging from coding challenges to scientific reasoning and from language processing to creative problem-solving. Key findings include: -83.3% success rate in solving complex competitive programming problems, surpassing many human experts. -Superior ability in generating coherent and accurate radiology reports, outperforming other evaluated models. -100% accuracy in high school-level mathematical reasoning tasks, providing detailed step-by-step solutions. -Advanced natural language inference capabilities across general and specialized domains like medicine. -Impressive performance in chip design tasks, outperforming specialized models in areas such as EDA script generation and bug analysis. -Remarkable proficiency in anthropology and geology, demonstrating deep understanding and reasoning in these specialized fields. -Strong capabilities in quantitative investing. O1 has comprehensive financial knowledge and statistical modeling skills. -Effective performance in social media analysis, including sentiment analysis and emotion recognition. The model excelled particularly in tasks requiring intricate reasoning and knowledge integration across various fields. While some limitations were observed, including occasional errors on simpler problems and challenges with certain highly specialized concepts, the overall results indicate significant progress towards artificial general intelligence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge