A Deep Bayesian Nonparametric Framework for Robust Mutual Information Estimation

Mutual Information (MI) is a crucial measure for capturing dependencies between variables, but exact computation is challenging in high dimensions with intractable likelihoods, impacting accuracy and robustness. One idea is to use an auxiliary neural network to train an MI estimator; however, methods based on the empirical distribution function (EDF) can introduce sharp fluctuations in the MI loss due to poor out-of-sample performance, destabilizing convergence. We present a Bayesian nonparametric (BNP) solution for training an MI estimator by constructing the MI loss with a finite representation of the Dirichlet process posterior to incorporate regularization in the training process. With this regularization, the MI loss integrates both prior knowledge and empirical data to reduce the loss sensitivity to fluctuations and outliers in the sample data, especially in small sample settings like mini-batches. This approach addresses the challenge of balancing accuracy and low variance by effectively reducing variance, leading to stabilized and robust MI loss gradients during training and enhancing the convergence of the MI approximation while offering stronger theoretical guarantees for convergence. We explore the application of our estimator in maximizing MI between the data space and the latent space of a variational autoencoder. Experimental results demonstrate significant improvements in convergence over EDF-based methods, with applications across synthetic and real datasets, notably in 3D CT image generation, yielding enhanced structure discovery and reduced overfitting in data synthesis. While this paper focuses on generative models in application, the proposed estimator is not restricted to this setting and can be applied more broadly in various BNP learning procedures.

Multi-View Oriented GPLVM: Expressiveness and Efficiency

The multi-view Gaussian process latent variable model (MV-GPLVM) aims to learn a unified representation from multi-view data but is hindered by challenges such as limited kernel expressiveness and low computational efficiency. To overcome these issues, we first introduce a new duality between the spectral density and the kernel function. By modeling the spectral density with a bivariate Gaussian mixture, we then derive a generic and expressive kernel termed Next-Gen Spectral Mixture (NG-SM) for MV-GPLVMs. To address the inherent computational inefficiency of the NG-SM kernel, we propose a random Fourier feature approximation. Combined with a tailored reparameterization trick, this approximation enables scalable variational inference for both the model and the unified latent representations. Numerical evaluations across a diverse range of multi-view datasets demonstrate that our proposed method consistently outperforms state-of-the-art models in learning meaningful latent representations.

Scalable Random Feature Latent Variable Models

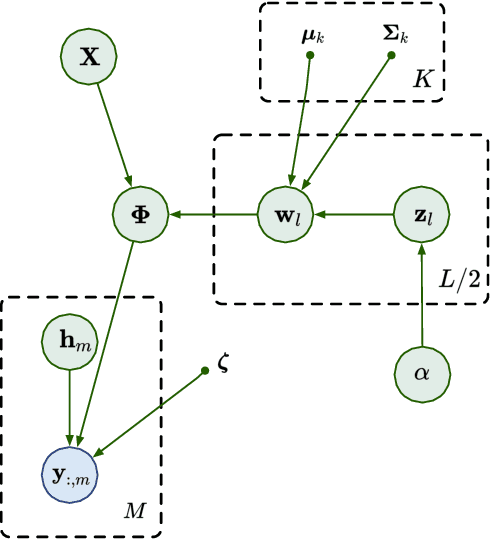
Random feature latent variable models (RFLVMs) represent the state-of-the-art in latent variable models, capable of handling non-Gaussian likelihoods and effectively uncovering patterns in high-dimensional data. However, their heavy reliance on Monte Carlo sampling results in scalability issues which makes it difficult to use these models for datasets with a massive number of observations. To scale up RFLVMs, we turn to the optimization-based variational Bayesian inference (VBI) algorithm which is known for its scalability compared to sampling-based methods. However, implementing VBI for RFLVMs poses challenges, such as the lack of explicit probability distribution functions (PDFs) for the Dirichlet process (DP) in the kernel learning component, and the incompatibility of existing VBI algorithms with RFLVMs. To address these issues, we introduce a stick-breaking construction for DP to obtain an explicit PDF and a novel VBI algorithm called ``block coordinate descent variational inference" (BCD-VI). This enables the development of a scalable version of RFLVMs, or in short, SRFLVM. Our proposed method shows scalability, computational efficiency, superior performance in generating informative latent representations and the ability of imputing missing data across various real-world datasets, outperforming state-of-the-art competitors.

Preventing Model Collapse in Gaussian Process Latent Variable Models

Gaussian process latent variable models (GPLVMs) are a versatile family of unsupervised learning models, commonly used for dimensionality reduction. However, common challenges in modeling data with GPLVMs include inadequate kernel flexibility and improper selection of the projection noise, which leads to a type of model collapse characterized primarily by vague latent representations that do not reflect the underlying structure of the data. This paper addresses these issues by, first, theoretically examining the impact of the projection variance on model collapse through the lens of a linear GPLVM. Second, we address the problem of model collapse due to inadequate kernel flexibility by integrating the spectral mixture (SM) kernel and a differentiable random Fourier feature (RFF) kernel approximation, which ensures computational scalability and efficiency through off-the-shelf automatic differentiation tools for learning the kernel hyperparameters, projection variance, and latent representations within the variational inference framework. The proposed GPLVM, named advisedRFLVM, is evaluated across diverse datasets and consistently outperforms various salient competing models, including state-of-the-art variational autoencoders (VAEs) and GPLVM variants, in terms of informative latent representations and missing data imputation.

Online Student-$t$ Processes with an Overall-local Scale Structure for Modelling Non-stationary Data

Time-dependent data often exhibit characteristics, such as non-stationarity and heavy-tailed errors, that would be inappropriate to model with the typical assumptions used in popular models. Thus, more flexible approaches are required to be able to accommodate such issues. To this end, we propose a Bayesian mixture of student-$t$ processes with an overall-local scale structure for the covariance. Moreover, we use a sequential Monte Carlo (SMC) sampler in order to perform online inference as data arrive in real-time. We demonstrate the superiority of our proposed approach compared to typical Gaussian process-based models on real-world data sets in order to prove the necessity of using mixtures of student-$t$ processes.

A Bayesian Non-parametric Approach to Generative Models: Integrating Variational Autoencoder and Generative Adversarial Networks using Wasserstein and Maximum Mean Discrepancy

Generative models have emerged as a promising technique for producing high-quality images that are indistinguishable from real images. Generative adversarial networks (GANs) and variational autoencoders (VAEs) are two of the most prominent and widely studied generative models. GANs have demonstrated excellent performance in generating sharp realistic images and VAEs have shown strong abilities to generate diverse images. However, GANs suffer from ignoring a large portion of the possible output space which does not represent the full diversity of the target distribution, and VAEs tend to produce blurry images. To fully capitalize on the strengths of both models while mitigating their weaknesses, we employ a Bayesian non-parametric (BNP) approach to merge GANs and VAEs. Our procedure incorporates both Wasserstein and maximum mean discrepancy (MMD) measures in the loss function to enable effective learning of the latent space and generate diverse and high-quality samples. By fusing the discriminative power of GANs with the reconstruction capabilities of VAEs, our novel model achieves superior performance in various generative tasks, such as anomaly detection and data augmentation. Furthermore, we enhance the model's capability by employing an extra generator in the code space, which enables us to explore areas of the code space that the VAE might have overlooked. With a BNP perspective, we can model the data distribution using an infinite-dimensional space, which provides greater flexibility in the model and reduces the risk of overfitting. By utilizing this framework, we can enhance the performance of both GANs and VAEs to create a more robust generative model suitable for various applications.

Bayesian Non-linear Latent Variable Modeling via Random Fourier Features

The Gaussian process latent variable model (GPLVM) is a popular probabilistic method used for nonlinear dimension reduction, matrix factorization, and state-space modeling. Inference for GPLVMs is computationally tractable only when the data likelihood is Gaussian. Moreover, inference for GPLVMs has typically been restricted to obtaining maximum a posteriori point estimates, which can lead to overfitting, or variational approximations, which mischaracterize the posterior uncertainty. Here, we present a method to perform Markov chain Monte Carlo (MCMC) inference for generalized Bayesian nonlinear latent variable modeling. The crucial insight necessary to generalize GPLVMs to arbitrary observation models is that we approximate the kernel function in the Gaussian process mappings with random Fourier features; this allows us to compute the gradient of the posterior in closed form with respect to the latent variables. We show that we can generalize GPLVMs to non-Gaussian observations, such as Poisson, negative binomial, and multinomial distributions, using our random feature latent variable model (RFLVM). Our generalized RFLVMs perform on par with state-of-the-art latent variable models on a wide range of applications, including motion capture, images, and text data for the purpose of estimating the latent structure and imputing the missing data of these complex data sets.

A Semi-Bayesian Nonparametric Hypothesis Test Using Maximum Mean Discrepancy with Applications in Generative Adversarial Networks

A classic inferential problem in statistics is the two-sample hypothesis test, where we test whether two samples of observations are either drawn from the same distribution or two distinct distributions. However, standard methods for performing this test require strong distributional assumptions on the two samples of data. We propose a semi-Bayesian nonparametric (semi-BNP) procedure for the two-sample hypothesis testing problem. First, we will derive a novel BNP maximum mean discrepancy (MMD) measure-based hypothesis test. Next, we will show that our proposed test will outperform frequentist MMD-based methods by yielding a smaller false rejection and acceptance rate of the null. Finally, we will show that we can embed our proposed hypothesis testing procedure within a generative adversarial network (GAN) framework as an application of our method. Using our novel BNP hypothesis test, this new GAN approach can help to mitigate the lack of diversity in the generated samples and produce a more accurate inferential algorithm compared to traditional techniques.

Sparse Infinite Random Feature Latent Variable Modeling

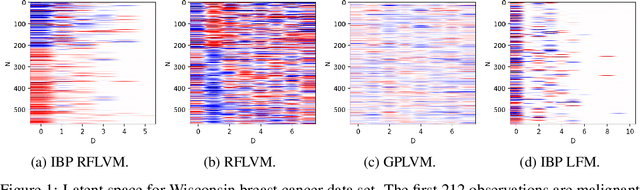
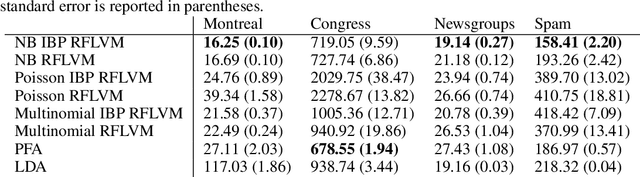
We propose a non-linear, Bayesian non-parametric latent variable model where the latent space is assumed to be sparse and infinite dimensional a priori using an Indian buffet process prior. A posteriori, the number of instantiated dimensions in the latent space is guaranteed to be finite. The purpose of placing the Indian buffet process on the latent variables is to: 1.) Automatically and probabilistically select the number of latent dimensions. 2.) Impose sparsity in the latent space, where the Indian buffet process will select which elements are exactly zero. Our proposed model allows for sparse, non-linear latent variable modeling where the number of latent dimensions is selected automatically. Inference is made tractable using the random Fourier approximation and we can easily implement posterior inference through Markov chain Monte Carlo sampling. This approach is amenable to many observation models beyond the Gaussian setting. We demonstrate the utility of our method on a variety of synthetic, biological and text datasets and show that we can obtain superior test set performance compared to previous latent variable models.

Accelerated Algorithms for Convex and Non-Convex Optimization on Manifolds

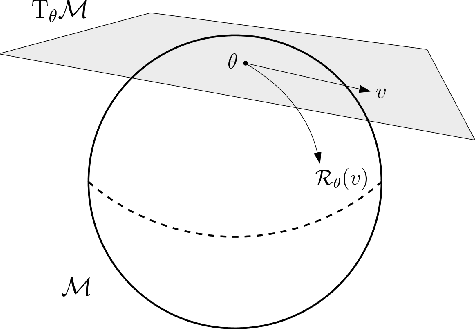
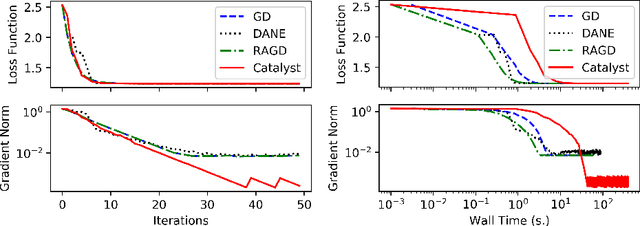
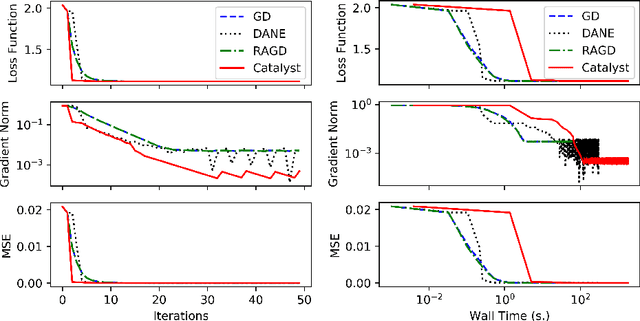
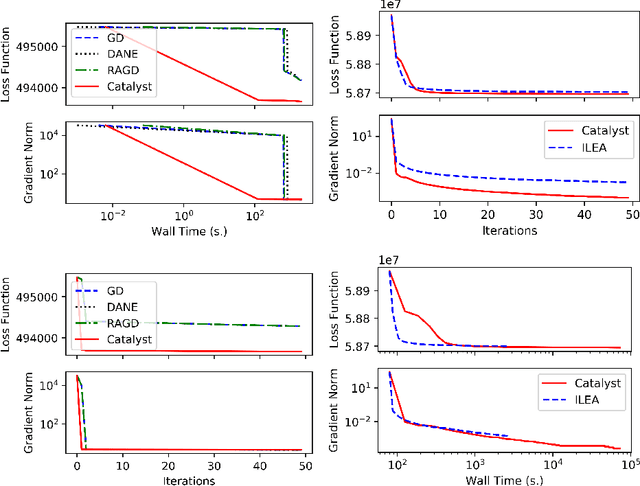
We propose a general scheme for solving convex and non-convex optimization problems on manifolds. The central idea is that, by adding a multiple of the squared retraction distance to the objective function in question, we "convexify" the objective function and solve a series of convex sub-problems in the optimization procedure. One of the key challenges for optimization on manifolds is the difficulty of verifying the complexity of the objective function, e.g., whether the objective function is convex or non-convex, and the degree of non-convexity. Our proposed algorithm adapts to the level of complexity in the objective function. We show that when the objective function is convex, the algorithm provably converges to the optimum and leads to accelerated convergence. When the objective function is non-convex, the algorithm will converge to a stationary point. Our proposed method unifies insights from Nesterov's original idea for accelerating gradient descent algorithms with recent developments in optimization algorithms in Euclidean space. We demonstrate the utility of our algorithms on several manifold optimization tasks such as estimating intrinsic and extrinsic Fr\'echet means on spheres and low-rank matrix factorization with Grassmann manifolds applied to the Netflix rating data set.