Tangent Space Causal Inference: Leveraging Vector Fields for Causal Discovery in Dynamical Systems

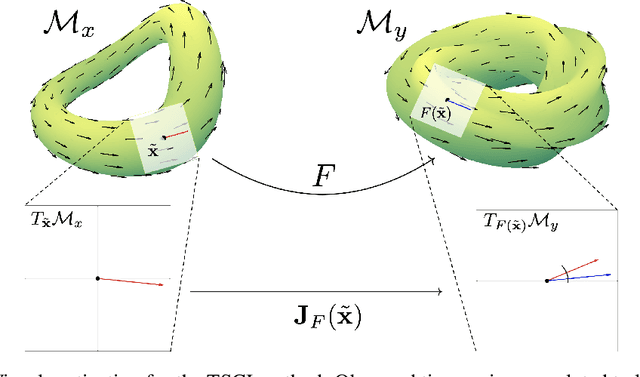
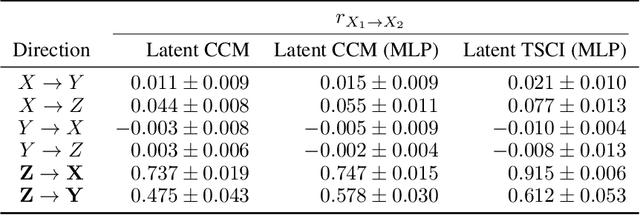
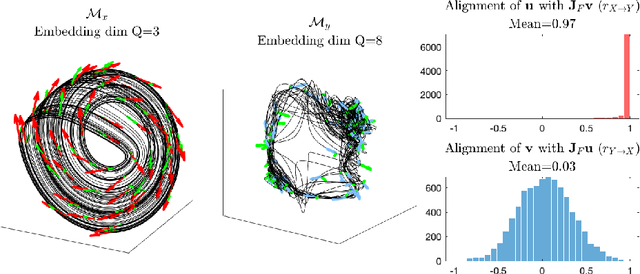
Causal discovery with time series data remains a challenging yet increasingly important task across many scientific domains. Convergent cross mapping (CCM) and related methods have been proposed to study time series that are generated by dynamical systems, where traditional approaches like Granger causality are unreliable. However, CCM often yields inaccurate results depending upon the quality of the data. We propose the Tangent Space Causal Inference (TSCI) method for detecting causalities in dynamical systems. TSCI works by considering vector fields as explicit representations of the systems' dynamics and checks for the degree of synchronization between the learned vector fields. The TSCI approach is model-agnostic and can be used as a drop-in replacement for CCM and its generalizations. We first present a basic version of the TSCI algorithm, which is shown to be more effective than the basic CCM algorithm with very little additional computation. We additionally present augmented versions of TSCI that leverage the expressive power of latent variable models and deep learning. We validate our theory on standard systems, and we demonstrate improved causal inference performance across a number of benchmark tasks.

Scalable Random Feature Latent Variable Models

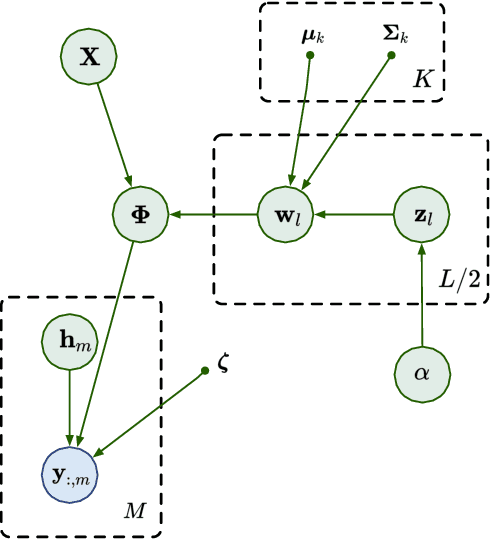
Random feature latent variable models (RFLVMs) represent the state-of-the-art in latent variable models, capable of handling non-Gaussian likelihoods and effectively uncovering patterns in high-dimensional data. However, their heavy reliance on Monte Carlo sampling results in scalability issues which makes it difficult to use these models for datasets with a massive number of observations. To scale up RFLVMs, we turn to the optimization-based variational Bayesian inference (VBI) algorithm which is known for its scalability compared to sampling-based methods. However, implementing VBI for RFLVMs poses challenges, such as the lack of explicit probability distribution functions (PDFs) for the Dirichlet process (DP) in the kernel learning component, and the incompatibility of existing VBI algorithms with RFLVMs. To address these issues, we introduce a stick-breaking construction for DP to obtain an explicit PDF and a novel VBI algorithm called ``block coordinate descent variational inference" (BCD-VI). This enables the development of a scalable version of RFLVMs, or in short, SRFLVM. Our proposed method shows scalability, computational efficiency, superior performance in generating informative latent representations and the ability of imputing missing data across various real-world datasets, outperforming state-of-the-art competitors.

A Gaussian Process-based Streaming Algorithm for Prediction of Time Series With Regimes and Outliers

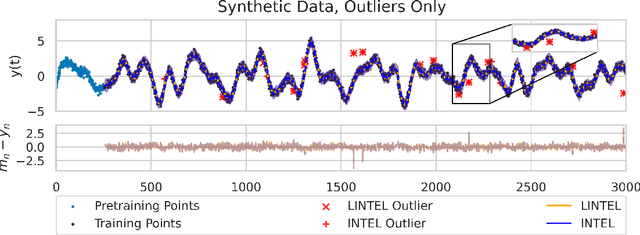
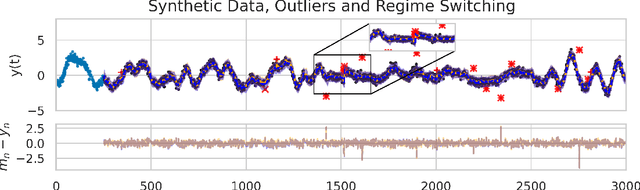
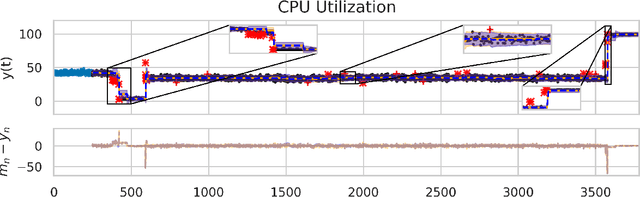
Online prediction of time series under regime switching is a widely studied problem in the literature, with many celebrated approaches. Using the non-parametric flexibility of Gaussian processes, the recently proposed INTEL algorithm provides a product of experts approach to online prediction of time series under possible regime switching, including the special case of outliers. This is achieved by adaptively combining several candidate models, each reporting their predictive distribution at time $t$. However, the INTEL algorithm uses a finite context window approximation to the predictive distribution, the computation of which scales cubically with the maximum lag, or otherwise scales quartically with exact predictive distributions. We introduce LINTEL, which uses the exact filtering distribution at time $t$ with constant-time updates, making the time complexity of the streaming algorithm optimal. We additionally note that the weighting mechanism of INTEL is better suited to a mixture of experts approach, and propose a fusion policy based on arithmetic averaging for LINTEL. We show experimentally that our proposed approach is over five times faster than INTEL under reasonable settings with better quality predictions.

A Deep-NN Beamforming Approach for Dual Function Radar-Communication THz UAV

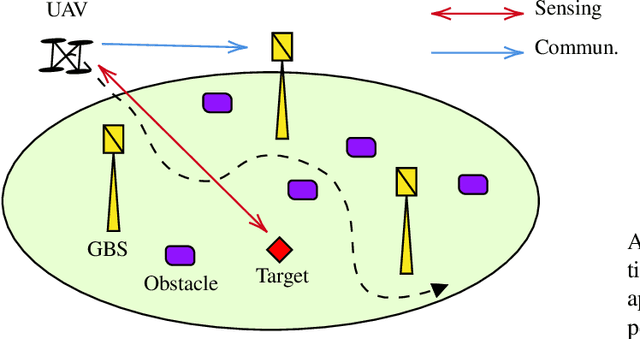
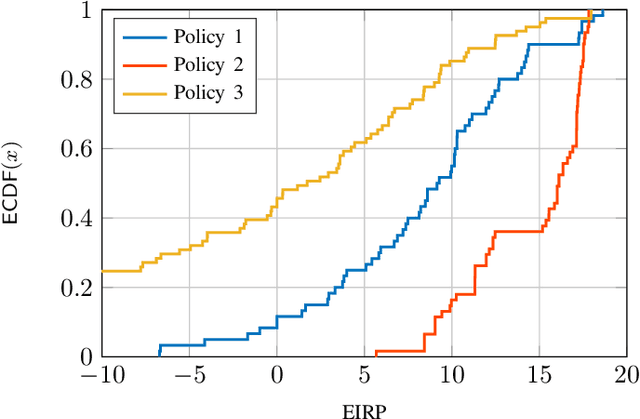
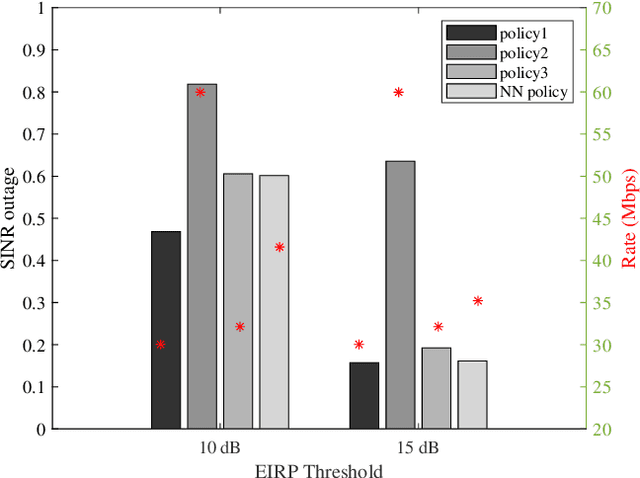
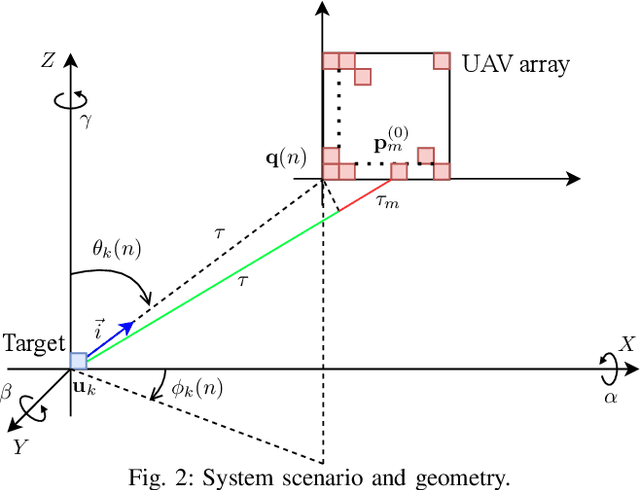
In this paper, we consider a scenario with one UAV equipped with a ULA, which sends combined information and sensing signals to communicate with multiple GBS and, at the same time, senses potential targets placed within an interested area on the ground. We aim to jointly design the transmit beamforming with the GBS association to optimize communication performance while ensuring high sensing accuracy. We propose a predictive beamforming framework based on a dual DNN solution to solve the formulated nonconvex optimization problem. A first DNN is trained to produce the required beamforming matrix for any point of the UAV flying area in a reduced time compared to state-of-the-art beamforming optimizers. A second DNN is trained to learn the optimal mapping from the input features, power, and EIRP constraints to the GBS association decision. Finally, we provide an extensive simulation analysis to corroborate the proposed approach and show the benefits of EIRP, SINR performance and computational speed.

Dynamic Online Ensembles of Basis Expansions

Practical Bayesian learning often requires (1) online inference, (2) dynamic models, and (3) ensembling over multiple different models. Recent advances have shown how to use random feature approximations to achieve scalable, online ensembling of Gaussian processes with desirable theoretical properties and fruitful applications. One key to these methods' success is the inclusion of a random walk on the model parameters, which makes models dynamic. We show that these methods can be generalized easily to any basis expansion model and that using alternative basis expansions, such as Hilbert space Gaussian processes, often results in better performance. To simplify the process of choosing a specific basis expansion, our method's generality also allows the ensembling of several entirely different models, for example, a Gaussian process and polynomial regression. Finally, we propose a novel method to ensemble static and dynamic models together.

Fusion of Probability Density Functions

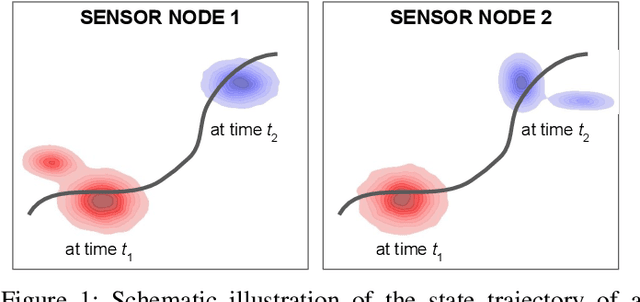
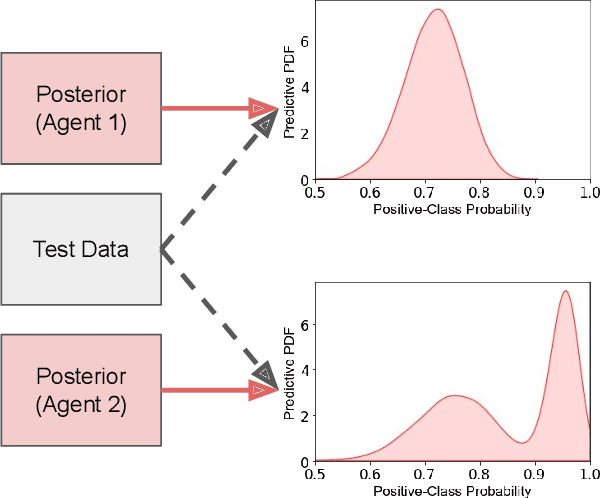
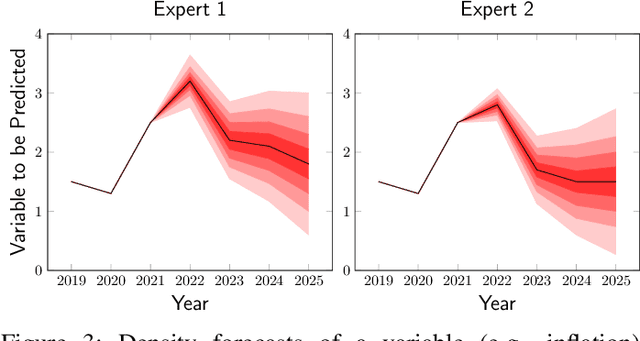
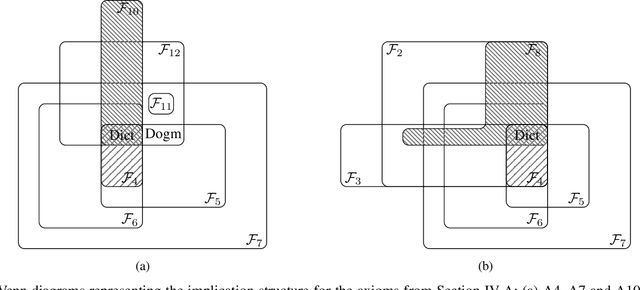
Fusing probabilistic information is a fundamental task in signal and data processing with relevance to many fields of technology and science. In this work, we investigate the fusion of multiple probability density functions (pdfs) of a continuous random variable or vector. Although the case of continuous random variables and the problem of pdf fusion frequently arise in multisensor signal processing, statistical inference, and machine learning, a universally accepted method for pdf fusion does not exist. The diversity of approaches, perspectives, and solutions related to pdf fusion motivates a unified presentation of the theory and methodology of the field. We discuss three different approaches to fusing pdfs. In the axiomatic approach, the fusion rule is defined indirectly by a set of properties (axioms). In the optimization approach, it is the result of minimizing an objective function that involves an information-theoretic divergence or a distance measure. In the supra-Bayesian approach, the fusion center interprets the pdfs to be fused as random observations. Our work is partly a survey, reviewing in a structured and coherent fashion many of the concepts and methods that have been developed in the literature. In addition, we present new results for each of the three approaches. Our original contributions include new fusion rules, axioms, and axiomatic and optimization-based characterizations; a new formulation of supra-Bayesian fusion in terms of finite-dimensional parametrizations; and a study of supra-Bayesian fusion of posterior pdfs for linear Gaussian models.

Bayesian Reconstruction of Fourier Pairs

In a number of data-driven applications such as detection of arrhythmia, interferometry or audio compression, observations are acquired indistinctly in the time or frequency domains: temporal observations allow us to study the spectral content of signals (e.g., audio), while frequency-domain observations are used to reconstruct temporal/spatial data (e.g., MRI). Classical approaches for spectral analysis rely either on i) a discretisation of the time and frequency domains, where the fast Fourier transform stands out as the \textit{de facto} off-the-shelf resource, or ii) stringent parametric models with closed-form spectra. However, the general literature fails to cater for missing observations and noise-corrupted data. Our aim is to address the lack of a principled treatment of data acquired indistinctly in the temporal and frequency domains in a way that is robust to missing or noisy observations, and that at the same time models uncertainty effectively. To achieve this aim, we first define a joint probabilistic model for the temporal and spectral representations of signals, to then perform a Bayesian model update in the light of observations, thus jointly reconstructing the complete (latent) time and frequency representations. The proposed model is analysed from a classical spectral analysis perspective, and its implementation is illustrated through intuitive examples. Lastly, we show that the proposed model is able to perform joint time and frequency reconstruction of real-world audio, healthcare and astronomy signals, while successfully dealing with missing data and handling uncertainty (noise) naturally against both classical and modern approaches for spectral estimation.