Hybrid Data-Driven SSM for Interpretable and Label-Free mmWave Channel Prediction

Accurate prediction of mmWave time-varying channels is essential for mitigating the issue of channel aging in complex scenarios owing to high user mobility. Existing channel prediction methods have limitations: classical model-based methods often struggle to track highly nonlinear channel dynamics due to limited expert knowledge, while emerging data-driven methods typically require substantial labeled data for effective training and often lack interpretability. To address these issues, this paper proposes a novel hybrid method that integrates a data-driven neural network into a conventional model-based workflow based on a state-space model (SSM), implicitly tracking complex channel dynamics from data without requiring precise expert knowledge. Additionally, a novel unsupervised learning strategy is developed to train the embedded neural network solely with unlabeled data. Theoretical analyses and ablation studies are conducted to interpret the enhanced benefits gained from the hybrid integration. Numerical simulations based on the 3GPP mmWave channel model corroborate the superior prediction accuracy of the proposed method, compared to state-of-the-art methods that are either purely model-based or data-driven. Furthermore, extensive experiments validate its robustness against various challenging factors, including among others severe channel variations and high noise levels.

Scalable Random Feature Latent Variable Models

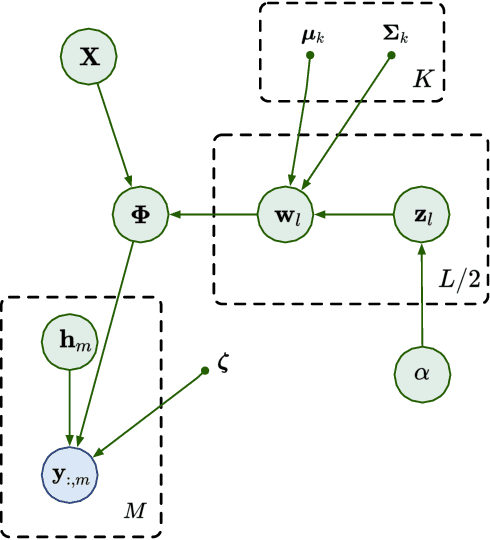
Random feature latent variable models (RFLVMs) represent the state-of-the-art in latent variable models, capable of handling non-Gaussian likelihoods and effectively uncovering patterns in high-dimensional data. However, their heavy reliance on Monte Carlo sampling results in scalability issues which makes it difficult to use these models for datasets with a massive number of observations. To scale up RFLVMs, we turn to the optimization-based variational Bayesian inference (VBI) algorithm which is known for its scalability compared to sampling-based methods. However, implementing VBI for RFLVMs poses challenges, such as the lack of explicit probability distribution functions (PDFs) for the Dirichlet process (DP) in the kernel learning component, and the incompatibility of existing VBI algorithms with RFLVMs. To address these issues, we introduce a stick-breaking construction for DP to obtain an explicit PDF and a novel VBI algorithm called ``block coordinate descent variational inference" (BCD-VI). This enables the development of a scalable version of RFLVMs, or in short, SRFLVM. Our proposed method shows scalability, computational efficiency, superior performance in generating informative latent representations and the ability of imputing missing data across various real-world datasets, outperforming state-of-the-art competitors.

Preventing Model Collapse in Gaussian Process Latent Variable Models

Gaussian process latent variable models (GPLVMs) are a versatile family of unsupervised learning models, commonly used for dimensionality reduction. However, common challenges in modeling data with GPLVMs include inadequate kernel flexibility and improper selection of the projection noise, which leads to a type of model collapse characterized primarily by vague latent representations that do not reflect the underlying structure of the data. This paper addresses these issues by, first, theoretically examining the impact of the projection variance on model collapse through the lens of a linear GPLVM. Second, we address the problem of model collapse due to inadequate kernel flexibility by integrating the spectral mixture (SM) kernel and a differentiable random Fourier feature (RFF) kernel approximation, which ensures computational scalability and efficiency through off-the-shelf automatic differentiation tools for learning the kernel hyperparameters, projection variance, and latent representations within the variational inference framework. The proposed GPLVM, named advisedRFLVM, is evaluated across diverse datasets and consistently outperforms various salient competing models, including state-of-the-art variational autoencoders (VAEs) and GPLVM variants, in terms of informative latent representations and missing data imputation.

Regularization-Based Efficient Continual Learning in Deep State-Space Models

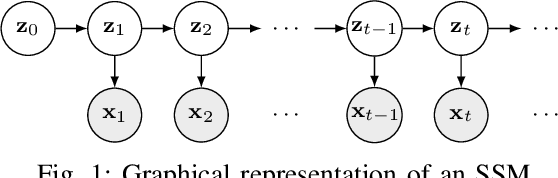
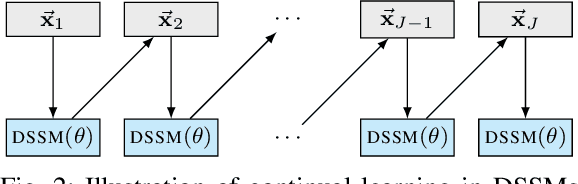
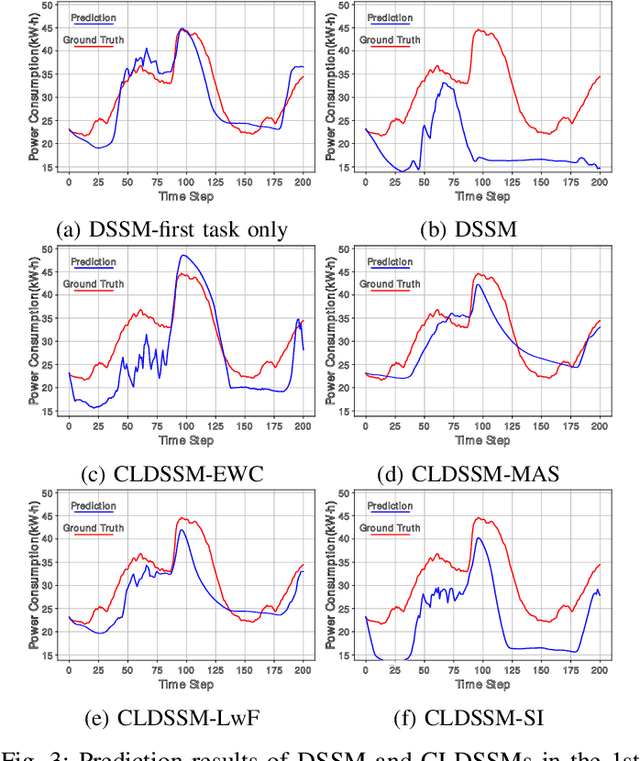
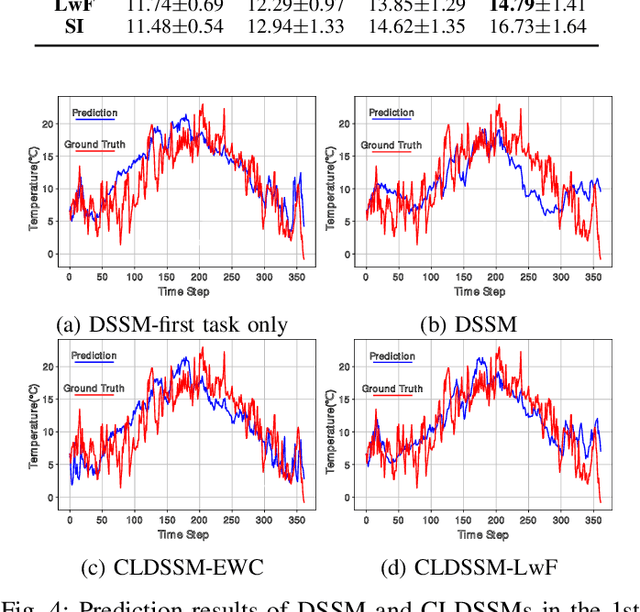
Deep state-space models (DSSMs) have gained popularity in recent years due to their potent modeling capacity for dynamic systems. However, existing DSSM works are limited to single-task modeling, which requires retraining with historical task data upon revisiting a forepassed task. To address this limitation, we propose continual learning DSSMs (CLDSSMs), which are capable of adapting to evolving tasks without catastrophic forgetting. Our proposed CLDSSMs integrate mainstream regularization-based continual learning (CL) methods, ensuring efficient updates with constant computational and memory costs for modeling multiple dynamic systems. We also conduct a comprehensive cost analysis of each CL method applied to the respective CLDSSMs, and demonstrate the efficacy of CLDSSMs through experiments on real-world datasets. The results corroborate that while various competing CL methods exhibit different merits, the proposed CLDSSMs consistently outperform traditional DSSMs in terms of effectively addressing catastrophic forgetting, enabling swift and accurate parameter transfer to new tasks.

Ensemble Kalman Filtering-Aided Variational Inference for Gaussian Process State-Space Models

Gaussian process state-space models (GPSSMs) are a flexible and principled approach for modeling dynamical systems. However, existing variational learning and inference methods for GPSSMs often necessitate optimizing a substantial number of variational distribution parameters, leading to inadequate performance and efficiency. To overcome this issue, we propose incorporating the ensemble Kalman filter (EnKF), a well-established model-based filtering technique, into the variational inference framework to approximate the posterior distribution of latent states. This utilization of EnKF can effectively exploit the dependencies between latent states and GP dynamics, while eliminating the need for parameterizing the variational distribution, thereby significantly reducing the number of variational parameters. Moreover, we show that our proposed algorithm allows straightforward evaluation of an approximated evidence lower bound (ELBO) in variational inference via simply summating multiple terms with readily available closed-form solutions. Leveraging automatic differentiation tools, we hence can maximize the ELBO and train the GPSSM efficiently. We also extend the proposed algorithm to an online setting and provide detailed algorithmic analyses and insights. Extensive evaluation on diverse real and synthetic datasets demonstrates the superiority of our EnKF-aided variational inference algorithms in terms of learning and inference performance compared to existing methods.

Gaussian Processes with Linear Multiple Kernel: Spectrum Design and Distributed Learning for Multi-Dimensional Data

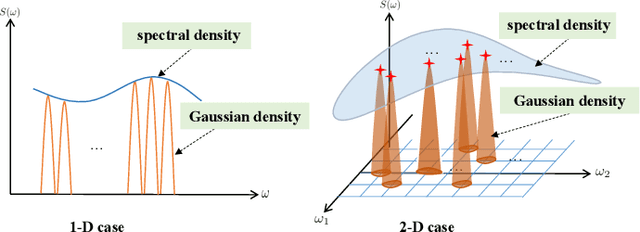
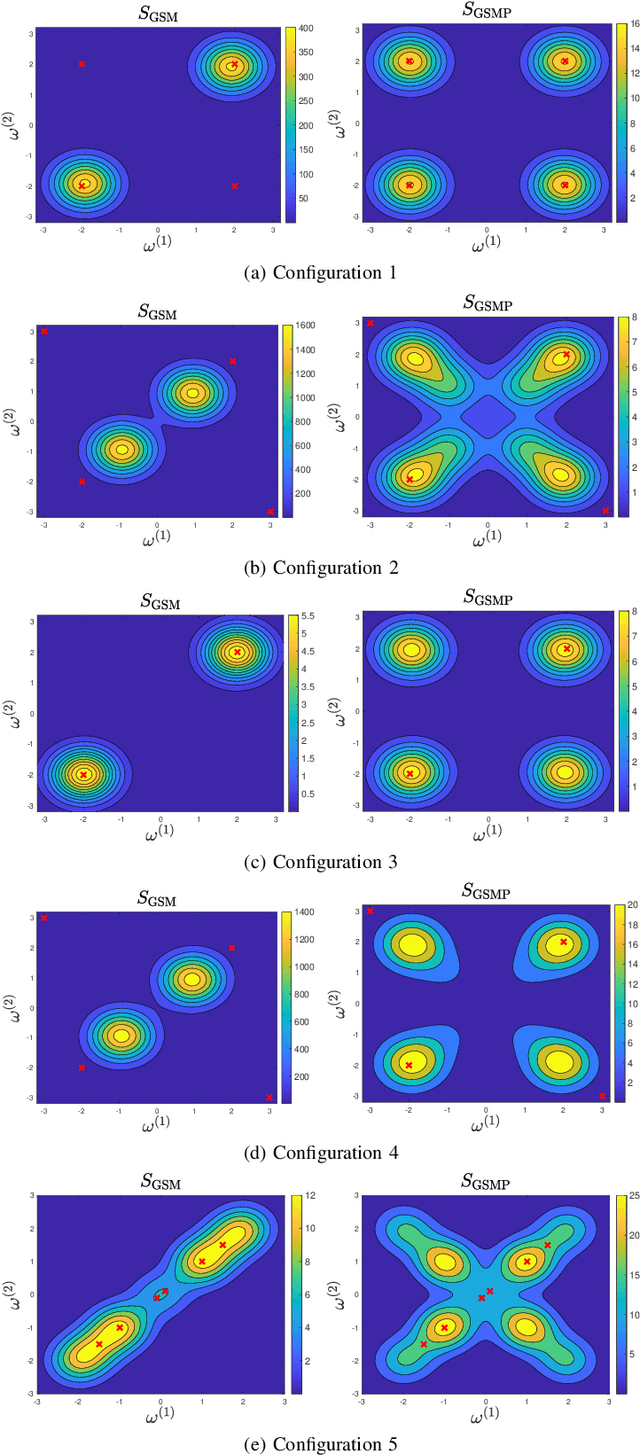
Gaussian processes (GPs) have emerged as a prominent technique for machine learning and signal processing. A key component in GP modeling is the choice of kernel, and linear multiple kernels (LMKs) have become an attractive kernel class due to their powerful modeling capacity and interpretability. This paper focuses on the grid spectral mixture (GSM) kernel, an LMK that can approximate arbitrary stationary kernels. Specifically, we propose a novel GSM kernel formulation for multi-dimensional data that reduces the number of hyper-parameters compared to existing formulations, while also retaining a favorable optimization structure and approximation capability. In addition, to make the large-scale hyper-parameter optimization in the GSM kernel tractable, we first introduce the distributed SCA (DSCA) algorithm. Building on this, we propose the doubly distributed SCA (D$^2$SCA) algorithm based on the alternating direction method of multipliers (ADMM) framework, which allows us to cooperatively learn the GSM kernel in the context of big data while maintaining data privacy. Furthermore, we tackle the inherent communication bandwidth restriction in distributed frameworks, by quantizing the hyper-parameters in D$^2$SCA, resulting in the quantized doubly distributed SCA (QD$^2$SCA) algorithm. Theoretical analysis establishes convergence guarantees for the proposed algorithms, while experiments on diverse datasets demonstrate the superior prediction performance and efficiency of our methods.

Towards Efficient Modeling and Inference in Multi-Dimensional Gaussian Process State-Space Models

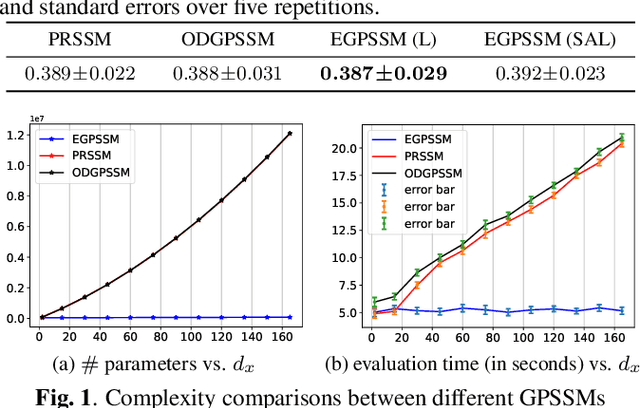
The Gaussian process state-space model (GPSSM) has attracted extensive attention for modeling complex nonlinear dynamical systems. However, the existing GPSSM employs separate Gaussian processes (GPs) for each latent state dimension, leading to escalating computational complexity and parameter proliferation, thus posing challenges for modeling dynamical systems with high-dimensional latent states. To surmount this obstacle, we propose to integrate the efficient transformed Gaussian process (ETGP) into the GPSSM, which involves pushing a shared GP through multiple normalizing flows to efficiently model the transition function in high-dimensional latent state space. Additionally, we develop a corresponding variational inference algorithm that surpasses existing methods in terms of parameter count and computational complexity. Experimental results on diverse synthetic and real-world datasets corroborate the efficiency of the proposed method, while also demonstrating its ability to achieve similar inference performance compared to existing methods. Code is available at \url{https://github.com/zhidilin/gpssmProj}.

Output-Dependent Gaussian Process State-Space Model

Gaussian process state-space model (GPSSM) is a fully probabilistic state-space model that has attracted much attention over the past decade. However, the outputs of the transition function in the existing GPSSMs are assumed to be independent, meaning that the GPSSMs cannot exploit the inductive biases between different outputs and lose certain model capacities. To address this issue, this paper proposes an output-dependent and more realistic GPSSM by utilizing the well-known, simple yet practical linear model of coregionalization (LMC) framework to represent the output dependency. To jointly learn the output-dependent GPSSM and infer the latent states, we propose a variational sparse GP-based learning method that only gently increases the computational complexity. Experiments on both synthetic and real datasets demonstrate the superiority of the output-dependent GPSSM in terms of learning and inference performance.

Graph Neural Network for Large-Scale Network Localization

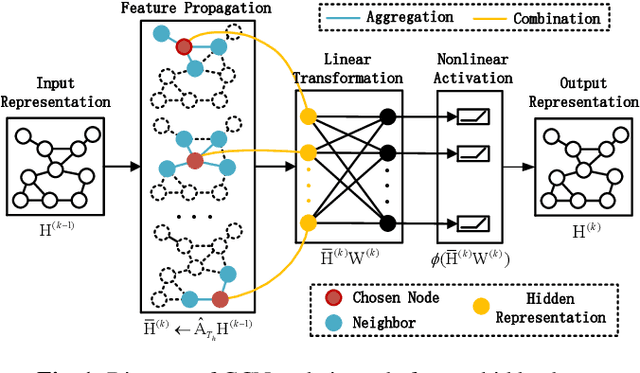
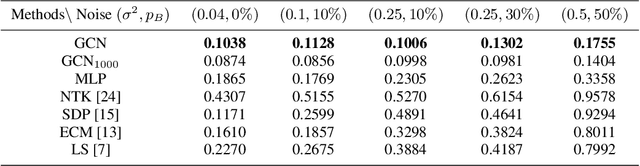
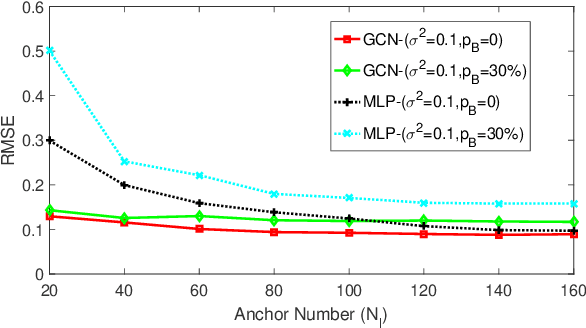
Graph neural networks (GNNs) are popular to use for classifying structured data in the context of machine learning. But surprisingly, they are rarely applied to regression problems. In this work, we adopt GNN for a classic but challenging nonlinear regression problem, namely the network localization. Our main findings are in order. First, GNN is potentially the best solution to large-scale network localization in terms of accuracy, robustness and computational time. Second, thresholding of the communication range is essential to its superior performance. Simulation results corroborate that the proposed GNN based method outperforms all benchmarks by far. Such inspiring results are further justified theoretically in terms of data aggregation, non-line-of-sight (NLOS) noise removal and lowpass filtering effect, all affected by the threshold for neighbor selection. Code is available at https://github.com/Yanzongzi/GNN-For-localization.

FedLoc: Federated Learning Framework for Cooperative Localization and Location Data Processing

In this paper, we propose a new localization framework in which mobile users or smart agents can cooperate to build accurate location services without sacrificing privacy, in particular, information related to their trajectories. The proposed framework is called Federated Localization (FedLoc), simply because it adopts the recently proposed federated learning. Apart from the new FedLoc framework, this paper can be deemed as an overview paper, in which we review the state-of-the-art federated learning framework, two widely used learning models, various distributed model hyper-parameter optimization schemes, and some practical use cases that fall under the FedLoc framework. The use cases, summarized from a mixture of standard, recently published, and unpublished works, cover a broad range of location services, including collaborative static localization/fingerprinting, indoor target tracking, outdoor navigation using low-sampling GPS, and spatio-temporal wireless traffic data modeling and prediction. The obtained primary results confirm that the proposed FedLoc framework well suits data-driven, machine learning-based localization and spatio-temporal data modeling. Future research directions are discussed at the end of this paper.