Hybrid Data-Driven SSM for Interpretable and Label-Free mmWave Channel Prediction

Accurate prediction of mmWave time-varying channels is essential for mitigating the issue of channel aging in complex scenarios owing to high user mobility. Existing channel prediction methods have limitations: classical model-based methods often struggle to track highly nonlinear channel dynamics due to limited expert knowledge, while emerging data-driven methods typically require substantial labeled data for effective training and often lack interpretability. To address these issues, this paper proposes a novel hybrid method that integrates a data-driven neural network into a conventional model-based workflow based on a state-space model (SSM), implicitly tracking complex channel dynamics from data without requiring precise expert knowledge. Additionally, a novel unsupervised learning strategy is developed to train the embedded neural network solely with unlabeled data. Theoretical analyses and ablation studies are conducted to interpret the enhanced benefits gained from the hybrid integration. Numerical simulations based on the 3GPP mmWave channel model corroborate the superior prediction accuracy of the proposed method, compared to state-of-the-art methods that are either purely model-based or data-driven. Furthermore, extensive experiments validate its robustness against various challenging factors, including among others severe channel variations and high noise levels.

Radar Anti-jamming Strategy Learning via Domain-knowledge Enhanced Online Convex Optimization

The dynamic competition between radar and jammer systems presents a significant challenge for modern Electronic Warfare (EW), as current active learning approaches still lack sample efficiency and fail to exploit jammer's characteristics. In this paper, the competition between a frequency agile radar and a Digital Radio Frequency Memory (DRFM)-based intelligent jammer is considered. We introduce an Online Convex Optimization (OCO) framework designed to illustrate this adversarial interaction. Notably, traditional OCO algorithms exhibit suboptimal sample efficiency due to the limited information obtained per round. To address the limitations, two refined algorithms are proposed, utilizing unbiased gradient estimators that leverage the unique attributes of the jammer system. Sub-linear theoretical results on both static regret and universal regret are provided, marking a significant improvement in OCO performance. Furthermore, simulation results reveal that the proposed algorithms outperform common OCO baselines, suggesting the potential for effective deployment in real-world scenarios.

Optimistic Thompson Sampling for No-Regret Learning in Unknown Games

This work tackles the complexities of multi-player scenarios in \emph{unknown games}, where the primary challenge lies in navigating the uncertainty of the environment through bandit feedback alongside strategic decision-making. We introduce Thompson Sampling (TS)-based algorithms that exploit the information of opponents' actions and reward structures, leading to a substantial reduction in experimental budgets -- achieving over tenfold improvements compared to conventional approaches. Notably, our algorithms demonstrate that, given specific reward structures, the regret bound depends logarithmically on the total action space, significantly alleviating the curse of multi-player. Furthermore, we unveil the \emph{Optimism-then-NoRegret} (OTN) framework, a pioneering methodology that seamlessly incorporates our advancements with established algorithms, showcasing its utility in practical scenarios such as traffic routing and radar sensing in the real world.

An Alternating Riemannian Gradient Algorithm for Fair Principal Component Analysis

Fair principal component analysis (FPCA), a ubiquitous dimensionality reduction technique in signal processing and machine learning, aims to find a low-dimensional representation for a high-dimensional dataset in view of fairness. The FPCA problem is a non-convex and non-smooth optimization over the Stiefel manifold. The state-of-the-art methods for solving the problem are subgradient methods and semidefinite relaxation based methods. However, these two types of methods have their obvious limitations and thus are only suitable for efficiently solving the FPCA problem in very special scenarios. The goal of this paper is to develop efficient algorithms for solving the FPCA problem in general settings, especially the very high-dimensional setting. In this paper, we first transform the problem into a smooth non-convex concave minimax optimization over the Stiefel manifold. Then we propose an alternating Riemannian gradient (ARG) algorithm, which performs a Riemannian gradient descent step and an ordinary gradient projection step at each iteration, for solving the general non-convex concave minimax problems over Riemannian manifolds. We prove that ARG can find an $\varepsilon$-stationary point of the above problem within $O(\varepsilon^{-4})$ iterations. Simulation results show that, compared with the state-of-the-art methods, our proposed ARG algorithm can achieve better performance in terms of the solution quality and speed for solving the FPCA problems arising from signal processing and machine learning.

Counterfactual Regret Minimization for Anti-jamming Game of Frequency Agile Radar

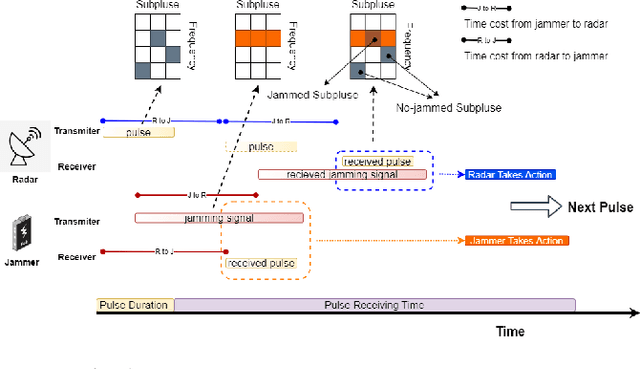
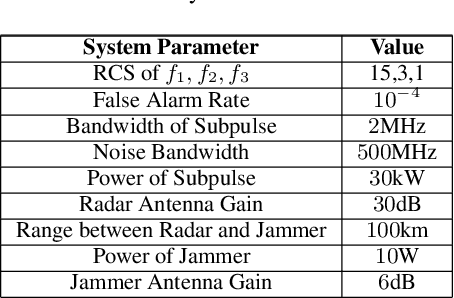
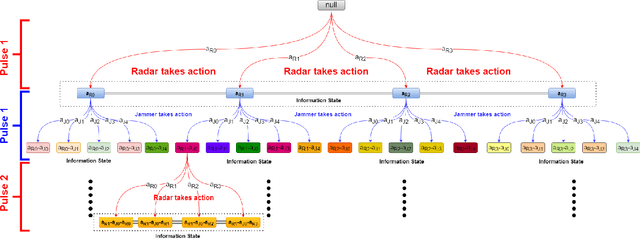
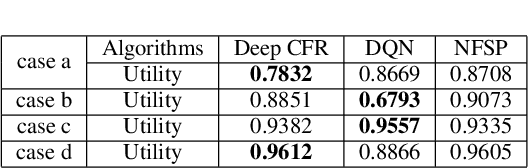
The competition between radar and jammer is one emerging issue in modern electronic warfare, which in principle can be viewed as a non-cooperative game with two players. In this work, the competition between a frequency agile (FA) radar and a noise-modulated jammer is considered. As modern FA radar adopts coherent processing with several pulses, the competition is hence in a multiple-round way where each pulse can be modeled as one round interaction between the radar and jammer. To capture such multiple-round property as well as imperfect information inside the game, i.e., radar and jammer are unable to know the upcoming signal, we propose an extensive-form game formulation for such competition. Since the number of game information states grows exponentially with respect to number of pulses, finding Nash Equilibrium (NE) strategies may be a computationally intractable task. To effectively solve the game, a learning-based algorithm called deep Counterfactual Regret Minimization (CFR) is utilized. Numerical simulations demonstrates the effectiveness of deep CFR algorithm for approximately finding NE and obtaining the best response strategy.

To Supervise or Not: How to Effectively Learn Wireless Interference Management Models?

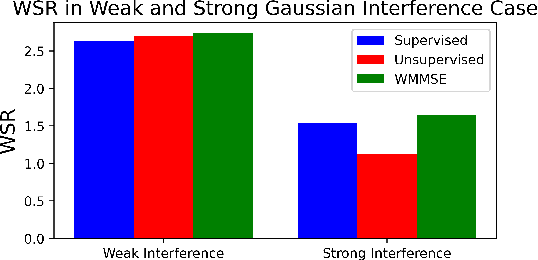
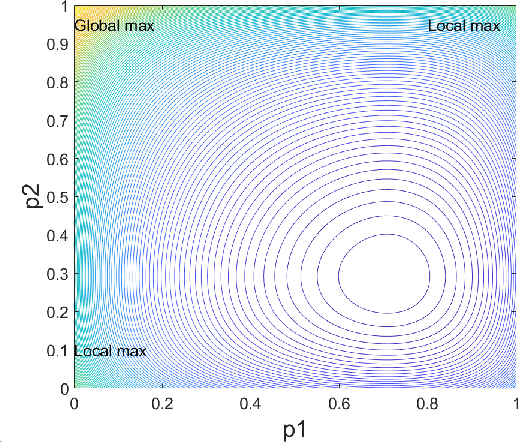
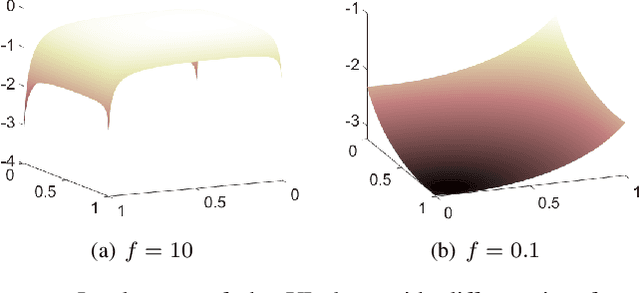
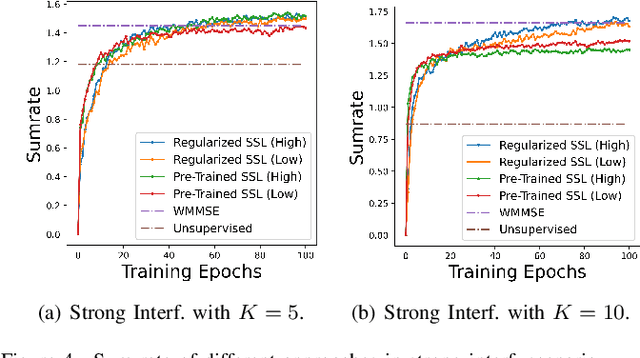
Machine learning has become successful in solving wireless interference management problems. Different kinds of deep neural networks (DNNs) have been trained to accomplish key tasks such as power control, beamforming and admission control. There are two popular training paradigms for such DNNs-based interference management models: supervised learning (i.e., fitting labels generated by an optimization algorithm) and unsupervised learning (i.e., directly optimizing some system performance measure). Although both of these paradigms have been extensively applied in practice, due to the lack of any theoretical understanding about these methods, it is not clear how to systematically understand and compare their performance. In this work, we conduct theoretical studies to provide some in-depth understanding about these two training paradigms. First, we show a somewhat surprising result, that for some special power control problem, the unsupervised learning can perform much worse than its supervised counterpart, because it is more likely to stuck at some low-quality local solutions. We then provide a series of theoretical results to further understand the properties of the two approaches. Generally speaking, we show that when high-quality labels are available, then the supervised learning is less likely to be stuck at a solution than its unsupervised counterpart. Additionally, we develop a semi-supervised learning approach which properly integrates these two training paradigms, and can effectively utilize limited number of labels to find high-quality solutions. To our knowledge, these are the first set of theoretical results trying to understand different training approaches in learning-based wireless communication system design.

Efficient Estimation of Sensor Biases for the 3-Dimensional Asynchronous Multi-Sensor System

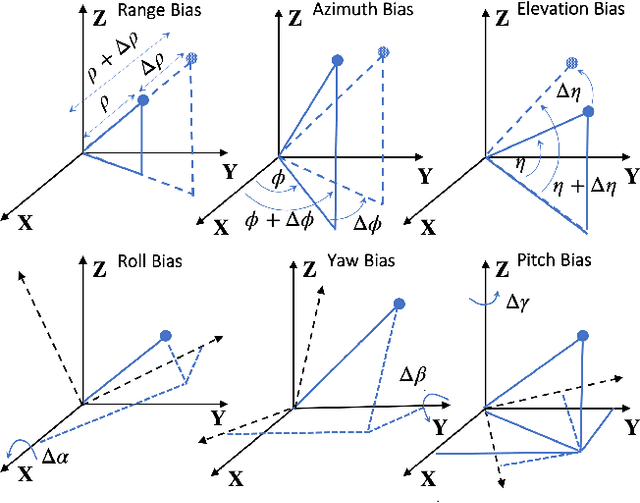
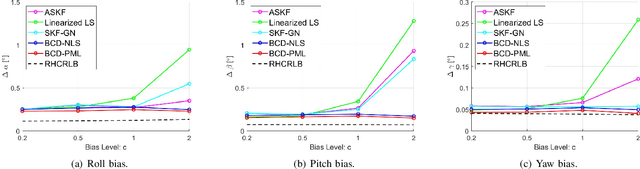
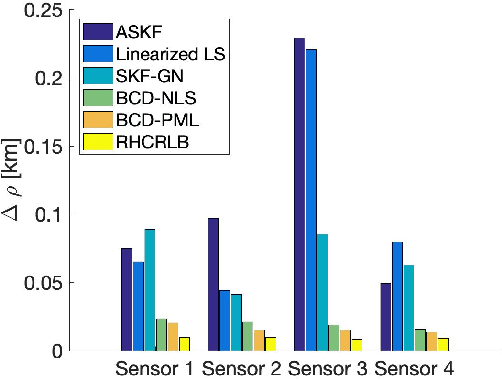
An important preliminary procedure in multi-sensor data fusion is sensor registration, and the key step in this procedure is to estimate sensor biases from their noisy measurements. There are generally two difficulties in this bias estimation problem: one is the unknown target states which serve as the nuisance variables in the estimation problem, and the other is the highly nonlinear coordinate transformation between the local and global coordinate systems of the sensors. In this paper, we focus on the 3-dimensional asynchronous multi-sensor scenario and propose a weighted nonlinear least squares (NLS) formulation by assuming that there is a target moving with a nearly constant velocity. We propose two possible choices of the weighting matrix in the NLS formulation, which correspond to classical NLS estimation and maximum likelihood (ML) estimation, respectively. To address the intrinsic nonlinearity, we propose a block coordinate descent (BCD) algorithm for solving the formulated problem, which alternately updates different kinds of bias estimates. Specifically, the proposed BCD algorithm involves solving linear LS problems and nonconvex quadratically constrained quadratic program (QCQP) problems with special structures. Instead of adopting the semidefinite relaxation technique, we develop a much more computationally efficient algorithm (with global performance guarantee under certain conditions) to solve the nonconvex QCQP subproblems. The effectiveness and efficiency of the proposed BCD algorithm are demonstrated via numerical simulations.

Learning to Continuously Optimize Wireless Resource in a Dynamic Environment: A Bilevel Optimization Perspective

There has been a growing interest in developing data-driven, and in particular deep neural network (DNN) based methods for modern communication tasks. For a few popular tasks such as power control, beamforming, and MIMO detection, these methods achieve state-of-the-art performance while requiring less computational efforts, less resources for acquiring channel state information (CSI), etc. However, it is often challenging for these approaches to learn in a dynamic environment. This work develops a new approach that enables data-driven methods to continuously learn and optimize resource allocation strategies in a dynamic environment. Specifically, we consider an ``episodically dynamic" setting where the environment statistics change in ``episodes", and in each episode the environment is stationary. We propose to build the notion of continual learning (CL) into wireless system design, so that the learning model can incrementally adapt to the new episodes, {\it without forgetting} knowledge learned from the previous episodes. Our design is based on a novel bilevel optimization formulation which ensures certain ``fairness" across different data samples. We demonstrate the effectiveness of the CL approach by integrating it with two popular DNN based models for power control and beamforming, respectively, and testing using both synthetic and ray-tracing based data sets. These numerical results show that the proposed CL approach is not only able to adapt to the new scenarios quickly and seamlessly, but importantly, it also maintains high performance over the previously encountered scenarios as well.

Stochastic Mirror Descent for Low-Rank Tensor Decomposition Under Non-Euclidean Losses

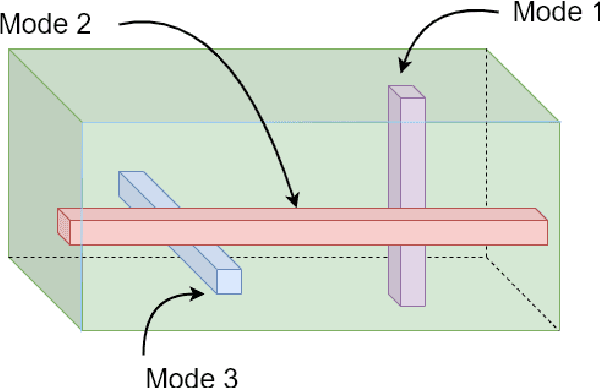
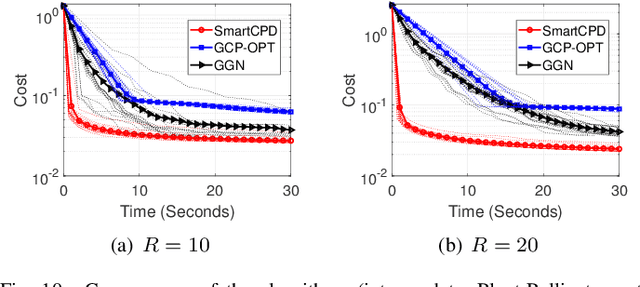
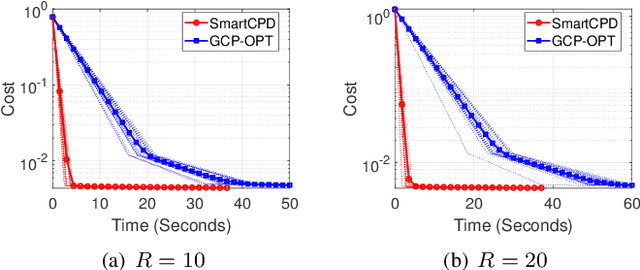
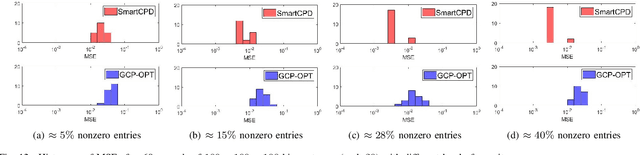
This work considers low-rank canonical polyadic decomposition (CPD) under a class of non-Euclidean loss functions that frequently arise in statistical machine learning and signal processing. These loss functions are often used for certain types of tensor data, e.g., count and binary tensors, where the least squares loss is considered unnatural.Compared to the least squares loss, the non-Euclidean losses are generally more challenging to handle. Non-Euclidean CPD has attracted considerable interests and a number of prior works exist. However, pressing computational and theoretical challenges, such as scalability and convergence issues, still remain. This work offers a unified stochastic algorithmic framework for large-scale CPD decomposition under a variety of non-Euclidean loss functions. Our key contribution lies in a tensor fiber sampling strategy-based flexible stochastic mirror descent framework. Leveraging the sampling scheme and the multilinear algebraic structure of low-rank tensors, the proposed lightweight algorithm ensures global convergence to a stationary point under reasonable conditions. Numerical results show that our framework attains promising non-Euclidean CPD performance. The proposed framework also exhibits substantial computational savings compared to state-of-the-art methods.

Learning to Continuously Optimize Wireless Resource In Episodically Dynamic Environment

There has been a growing interest in developing data-driven and in particular deep neural network (DNN) based methods for modern communication tasks. For a few popular tasks such as power control, beamforming, and MIMO detection, these methods achieve state-of-the-art performance while requiring less computational efforts, less channel state information (CSI), etc. However, it is often challenging for these approaches to learn in a dynamic environment where parameters such as CSIs keep changing. This work develops a methodology that enables data-driven methods to continuously learn and optimize in a dynamic environment. Specifically, we consider an ``episodically dynamic" setting where the environment changes in ``episodes", and in each episode the environment is stationary. We propose to build the notion of continual learning (CL) into the modeling process of learning wireless systems, so that the learning model can incrementally adapt to the new episodes, {\it without forgetting} knowledge learned from the previous episodes. Our design is based on a novel min-max formulation which ensures certain ``fairness" across different data samples. We demonstrate the effectiveness of the CL approach by customizing it to two popular DNN based models (one for power control and one for beamforming), and testing using both synthetic and real data sets. These numerical results show that the proposed CL approach is not only able to adapt to the new scenarios quickly and seamlessly, but importantly, it maintains high performance over the previously encountered scenarios as well.