Learning From Crowdsourced Noisy Labels: A Signal Processing Perspective

One of the primary catalysts fueling advances in artificial intelligence (AI) and machine learning (ML) is the availability of massive, curated datasets. A commonly used technique to curate such massive datasets is crowdsourcing, where data are dispatched to multiple annotators. The annotator-produced labels are then fused to serve downstream learning and inference tasks. This annotation process often creates noisy labels due to various reasons, such as the limited expertise, or unreliability of annotators, among others. Therefore, a core objective in crowdsourcing is to develop methods that effectively mitigate the negative impact of such label noise on learning tasks. This feature article introduces advances in learning from noisy crowdsourced labels. The focus is on key crowdsourcing models and their methodological treatments, from classical statistical models to recent deep learning-based approaches, emphasizing analytical insights and algorithmic developments. In particular, this article reviews the connections between signal processing (SP) theory and methods, such as identifiability of tensor and nonnegative matrix factorization, and novel, principled solutions of longstanding challenges in crowdsourcing -- showing how SP perspectives drive the advancements of this field. Furthermore, this article touches upon emerging topics that are critical for developing cutting-edge AI/ML systems, such as crowdsourcing in reinforcement learning with human feedback (RLHF) and direct preference optimization (DPO) that are key techniques for fine-tuning large language models (LLMs).

Under-Counted Tensor Completion with Neural Incorporation of Attributes

Systematic under-counting effects are observed in data collected across many disciplines, e.g., epidemiology and ecology. Under-counted tensor completion (UC-TC) is well-motivated for many data analytics tasks, e.g., inferring the case numbers of infectious diseases at unobserved locations from under-counted case numbers in neighboring regions. However, existing methods for similar problems often lack supports in theory, making it hard to understand the underlying principles and conditions beyond empirical successes. In this work, a low-rank Poisson tensor model with an expressive unknown nonlinear side information extractor is proposed for under-counted multi-aspect data. A joint low-rank tensor completion and neural network learning algorithm is designed to recover the model. Moreover, the UC-TC formulation is supported by theoretical analysis showing that the fully counted entries of the tensor and each entry's under-counting probability can be provably recovered from partial observations -- under reasonable conditions. To our best knowledge, the result is the first to offer theoretical supports for under-counted multi-aspect data completion. Simulations and real-data experiments corroborate the theoretical claims.

Deep Learning From Crowdsourced Labels: Coupled Cross-entropy Minimization, Identifiability, and Regularization

Using noisy crowdsourced labels from multiple annotators, a deep learning-based end-to-end (E2E) system aims to learn the label correction mechanism and the neural classifier simultaneously. To this end, many E2E systems concatenate the neural classifier with multiple annotator-specific ``label confusion'' layers and co-train the two parts in a parameter-coupled manner. The formulated coupled cross-entropy minimization (CCEM)-type criteria are intuitive and work well in practice. Nonetheless, theoretical understanding of the CCEM criterion has been limited. The contribution of this work is twofold: First, performance guarantees of the CCEM criterion are presented. Our analysis reveals for the first time that the CCEM can indeed correctly identify the annotators' confusion characteristics and the desired ``ground-truth'' neural classifier under realistic conditions, e.g., when only incomplete annotator labeling and finite samples are available. Second, based on the insights learned from our analysis, two regularized variants of the CCEM are proposed. The regularization terms provably enhance the identifiability of the target model parameters in various more challenging cases. A series of synthetic and real data experiments are presented to showcase the effectiveness of our approach.

Deep Clustering with Incomplete Noisy Pairwise Annotations: A Geometric Regularization Approach

The recent integration of deep learning and pairwise similarity annotation-based constrained clustering -- i.e., $\textit{deep constrained clustering}$ (DCC) -- has proven effective for incorporating weak supervision into massive data clustering: Less than 1% of pair similarity annotations can often substantially enhance the clustering accuracy. However, beyond empirical successes, there is a lack of understanding of DCC. In addition, many DCC paradigms are sensitive to annotation noise, but performance-guaranteed noisy DCC methods have been largely elusive. This work first takes a deep look into a recently emerged logistic loss function of DCC, and characterizes its theoretical properties. Our result shows that the logistic DCC loss ensures the identifiability of data membership under reasonable conditions, which may shed light on its effectiveness in practice. Building upon this understanding, a new loss function based on geometric factor analysis is proposed to fend against noisy annotations. It is shown that even under $\textit{unknown}$ annotation confusions, the data membership can still be $\textit{provably}$ identified under our proposed learning criterion. The proposed approach is tested over multiple datasets to validate our claims.

Crowdsourcing via Annotator Co-occurrence Imputation and Provable Symmetric Nonnegative Matrix Factorization

Unsupervised learning of the Dawid-Skene (D&S) model from noisy, incomplete and crowdsourced annotations has been a long-standing challenge, and is a critical step towards reliably labeling massive data. A recent work takes a coupled nonnegative matrix factorization (CNMF) perspective, and shows appealing features: It ensures the identifiability of the D\&S model and enjoys low sample complexity, as only the estimates of the co-occurrences of annotator labels are involved. However, the identifiability holds only when certain somewhat restrictive conditions are met in the context of crowdsourcing. Optimizing the CNMF criterion is also costly -- and convergence assurances are elusive. This work recasts the pairwise co-occurrence based D&S model learning problem as a symmetric NMF (SymNMF) problem -- which offers enhanced identifiability relative to CNMF. In practice, the SymNMF model is often (largely) incomplete, due to the lack of co-labeled items by some annotators. Two lightweight algorithms are proposed for co-occurrence imputation. Then, a low-complexity shifted rectified linear unit (ReLU)-empowered SymNMF algorithm is proposed to identify the D&S model. Various performance characterizations (e.g., missing co-occurrence recoverability, stability, and convergence) and evaluations are also presented.

Stochastic Mirror Descent for Low-Rank Tensor Decomposition Under Non-Euclidean Losses

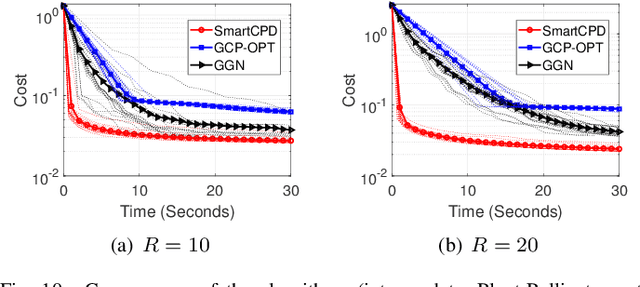
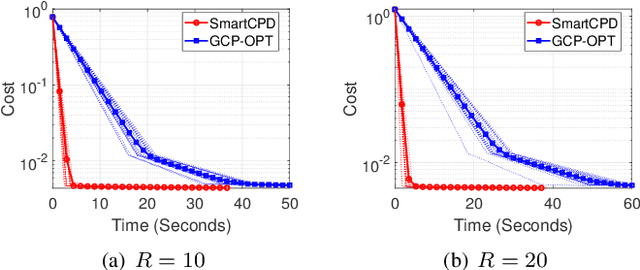
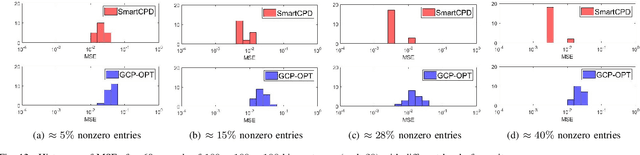
This work considers low-rank canonical polyadic decomposition (CPD) under a class of non-Euclidean loss functions that frequently arise in statistical machine learning and signal processing. These loss functions are often used for certain types of tensor data, e.g., count and binary tensors, where the least squares loss is considered unnatural.Compared to the least squares loss, the non-Euclidean losses are generally more challenging to handle. Non-Euclidean CPD has attracted considerable interests and a number of prior works exist. However, pressing computational and theoretical challenges, such as scalability and convergence issues, still remain. This work offers a unified stochastic algorithmic framework for large-scale CPD decomposition under a variety of non-Euclidean loss functions. Our key contribution lies in a tensor fiber sampling strategy-based flexible stochastic mirror descent framework. Leveraging the sampling scheme and the multilinear algebraic structure of low-rank tensors, the proposed lightweight algorithm ensures global convergence to a stationary point under reasonable conditions. Numerical results show that our framework attains promising non-Euclidean CPD performance. The proposed framework also exhibits substantial computational savings compared to state-of-the-art methods.

Mixed Membership Graph Clustering via Systematic Edge Query

This work considers clustering nodes of a largely incomplete graph. Under the problem setting, only a small amount of queries about the edges can be made, but the entire graph is not observable. This problem finds applications in large-scale data clustering using limited annotations, community detection under restricted survey resources, and graph topology inference under hidden/removed node interactions. Prior works treated this problem as a convex optimization-based matrix completion task. However, this line of work is designed for learning single cluster membership of nodes belonging to disjoint clusters, yet mixed (multiple) cluster membership nodes and overlapping clusters often arise in practice. Existing works also rely on the uniformly random edge query pattern and nuclear norm-based optimization, which give rise to a number of implementation and scalability challenges. This work aims at learning mixed membership of the nodes of overlapping clusters using edge queries. Our method offers membership learning guarantees under systematic query patterns (as opposed to random ones). The query patterns can be controlled and adjusted by the system designers to accommodate implementation challenges---e.g., to avoid querying edges that are physically hard to acquire. Our framework also features a lightweight and scalable algorithm. Real-data experiments on crowdclustering and community detection are used to showcase the effectiveness of our method.

Recovering Joint Probability of Discrete Random Variables from Pairwise Marginals

Learning the joint probability of random variables (RVs) lies at the heart of statistical signal processing and machine learning. However, direct nonparametric estimation for high-dimensional joint probability is in general impossible, due to the curse of dimensionality. Recent work has proposed to recover the joint probability mass function (PMF) of an arbitrary number of RVs from three-dimensional marginals, leveraging the algebraic properties of low-rank tensor decomposition and the (unknown) dependence among the RVs. Nonetheless, accurately estimating three-dimensional marginals can still be costly in terms of sample complexity, affecting the performance of this line of work in practice in the sample-starved regime. Using three-dimensional marginals also involves challenging tensor decomposition problems whose tractability is unclear. This work puts forth a new framework for learning the joint PMF using only pairwise marginals, which naturally enjoys a lower sample complexity relative to the third-order ones. A coupled nonnegative matrix factorization (CNMF) framework is developed, and its joint PMF recovery guarantees under various conditions are analyzed. Our method also features a Gram-Schmidt (GS)-like algorithm that exhibits competitive runtime performance. The algorithm is shown to provably recover the joint PMF up to bounded error in finite iterations, under reasonable conditions. It is also shown that a recently proposed economical expectation maximization (EM) algorithm guarantees to improve upon the GS-like algorithm's output, thereby further lifting up the accuracy and efficiency. Real-data experiments are employed to showcase the effectiveness.

On Recoverability of Randomly Compressed Tensors with Low CP Rank

Our interest lies in the recoverability properties of compressed tensors under the \textit{canonical polyadic decomposition} (CPD) model. The considered problem is well-motivated in many applications, e.g., hyperspectral image and video compression. Prior work studied this problem under somewhat special assumptions---e.g., the latent factors of the tensor are sparse or drawn from absolutely continuous distributions. We offer an alternative result: We show that if the tensor is compressed by a subgaussian linear mapping, then the tensor is recoverable if the number of measurements is on the same order of magnitude as that of the model parameters---without strong assumptions on the latent factors. Our proof is based on deriving a \textit{restricted isometry property} (R.I.P.) under the CPD model via set covering techniques, and thus exhibits a flavor of classic compressive sensing. The new recoverability result enriches the understanding to the compressed CP tensor recovery problem; it offers theoretical guarantees for recovering tensors whose elements are not necessarily continuous or sparse.

Crowdsourcing via Pairwise Co-occurrences: Identifiability and Algorithms

The data deluge comes with high demands for data labeling. Crowdsourcing (or, more generally, ensemble learning) techniques aim to produce accurate labels via integrating noisy, non-expert labeling from annotators. The classic Dawid-Skene estimator and its accompanying expectation maximization (EM) algorithm have been widely used, but the theoretical properties are not fully understood. Tensor methods were proposed to guarantee identification of the Dawid-Skene model, but the sample complexity is a hurdle for applying such approaches---since the tensor methods hinge on the availability of third-order statistics that are hard to reliably estimate given limited data. In this paper, we propose a framework using pairwise co-occurrences of the annotator responses, which naturally admits lower sample complexity. We show that the approach can identify the Dawid-Skene model under realistic conditions. We propose an algebraic algorithm reminiscent of convex geometry-based structured matrix factorization to solve the model identification problem efficiently, and an identifiability-enhanced algorithm for handling more challenging and critical scenarios. Experiments show that the proposed algorithms outperform the state-of-art algorithms under a variety of scenarios.