Provable Online CP/PARAFAC Decomposition of a Structured Tensor via Dictionary Learning

We consider the problem of factorizing a structured 3-way tensor into its constituent Canonical Polyadic (CP) factors. This decomposition, which can be viewed as a generalization of singular value decomposition (SVD) for tensors, reveals how the tensor dimensions (features) interact with each other. However, since the factors are a priori unknown, the corresponding optimization problems are inherently non-convex. The existing guaranteed algorithms which handle this non-convexity incur an irreducible error (bias), and only apply to cases where all factors have the same structure. To this end, we develop a provable algorithm for online structured tensor factorization, wherein one of the factors obeys some incoherence conditions, and the others are sparse. Specifically we show that, under some relatively mild conditions on initialization, rank, and sparsity, our algorithm recovers the factors exactly (up to scaling and permutation) at a linear rate. Complementary to our theoretical results, our synthetic and real-world data evaluations showcase superior performance compared to related techniques. Moreover, its scalability and ability to learn on-the-fly makes it suitable for real-world tasks.

The flare Package for High Dimensional Linear Regression and Precision Matrix Estimation in R

This paper describes an R package named flare, which implements a family of new high dimensional regression methods (LAD Lasso, SQRT Lasso, $\ell_q$ Lasso, and Dantzig selector) and their extensions to sparse precision matrix estimation (TIGER and CLIME). These methods exploit different nonsmooth loss functions to gain modeling flexibility, estimation robustness, and tuning insensitiveness. The developed solver is based on the alternating direction method of multipliers (ADMM). The package flare is coded in double precision C, and called from R by a user-friendly interface. The memory usage is optimized by using the sparse matrix output. The experiments show that flare is efficient and can scale up to large problems.

Picasso: A Sparse Learning Library for High Dimensional Data Analysis in R and Python

We describe a new library named picasso, which implements a unified framework of pathwise coordinate optimization for a variety of sparse learning problems (e.g., sparse linear regression, sparse logistic regression, sparse Poisson regression and scaled sparse linear regression) combined with efficient active set selection strategies. Besides, the library allows users to choose different sparsity-inducing regularizers, including the convex $\ell_1$, nonconvex MCP and SCAD regularizers. The library is coded in C++ and has user-friendly R and Python wrappers. Numerical experiments demonstrate that picasso can scale up to large problems efficiently.

Over-parameterized Adversarial Training: An Analysis Overcoming the Curse of Dimensionality

Adversarial training is a popular method to give neural nets robustness against adversarial perturbations. In practice adversarial training leads to low robust training loss. However, a rigorous explanation for why this happens under natural conditions is still missing. Recently a convergence theory for standard (non-adversarial) supervised training was developed by various groups for {\em very overparametrized} nets. It is unclear how to extend these results to adversarial training because of the min-max objective. Recently, a first step towards this direction was made by Gao et al. using tools from online learning, but they require the width of the net to be \emph{exponential} in input dimension $d$, and with an unnatural activation function. Our work proves convergence to low robust training loss for \emph{polynomial} width instead of exponential, under natural assumptions and with the ReLU activation. Key element of our proof is showing that ReLU networks near initialization can approximate the step function, which may be of independent interest.

On Computation and Generalization of Generative Adversarial Imitation Learning

Generative Adversarial Imitation Learning (GAIL) is a powerful and practical approach for learning sequential decision-making policies. Different from Reinforcement Learning (RL), GAIL takes advantage of demonstration data by experts (e.g., human), and learns both the policy and reward function of the unknown environment. Despite the significant empirical progresses, the theory behind GAIL is still largely unknown. The major difficulty comes from the underlying temporal dependency of the demonstration data and the minimax computational formulation of GAIL without convex-concave structure. To bridge such a gap between theory and practice, this paper investigates the theoretical properties of GAIL. Specifically, we show: (1) For GAIL with general reward parameterization, the generalization can be guaranteed as long as the class of the reward functions is properly controlled; (2) For GAIL, where the reward is parameterized as a reproducing kernel function, GAIL can be efficiently solved by stochastic first order optimization algorithms, which attain sublinear convergence to a stationary solution. To the best of our knowledge, these are the first results on statistical and computational guarantees of imitation learning with reward/policy function approximation. Numerical experiments are provided to support our analysis.

On Recoverability of Randomly Compressed Tensors with Low CP Rank

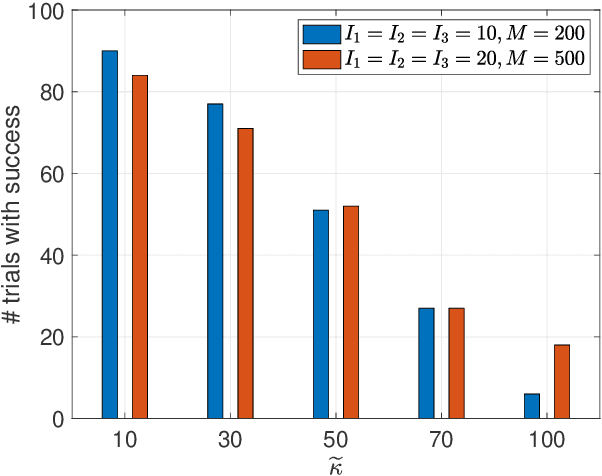
Our interest lies in the recoverability properties of compressed tensors under the \textit{canonical polyadic decomposition} (CPD) model. The considered problem is well-motivated in many applications, e.g., hyperspectral image and video compression. Prior work studied this problem under somewhat special assumptions---e.g., the latent factors of the tensor are sparse or drawn from absolutely continuous distributions. We offer an alternative result: We show that if the tensor is compressed by a subgaussian linear mapping, then the tensor is recoverable if the number of measurements is on the same order of magnitude as that of the model parameters---without strong assumptions on the latent factors. Our proof is based on deriving a \textit{restricted isometry property} (R.I.P.) under the CPD model via set covering techniques, and thus exhibits a flavor of classic compressive sensing. The new recoverability result enriches the understanding to the compressed CP tensor recovery problem; it offers theoretical guarantees for recovering tensors whose elements are not necessarily continuous or sparse.

On Generalization Bounds of a Family of Recurrent Neural Networks

Recurrent Neural Networks (RNNs) have been widely applied to sequential data analysis. Due to their complicated modeling structures, however, the theory behind is still largely missing. To connect theory and practice, we study the generalization properties of vanilla RNNs as well as their variants, including Minimal Gated Unit (MGU), Long Short Term Memory (LSTM), and Convolutional (Conv) RNNs. Specifically, our theory is established under the PAC-Learning framework. The generalization bound is presented in terms of the spectral norms of the weight matrices and the total number of parameters. We also establish refined generalization bounds with additional norm assumptions, and draw a comparison among these bounds. We remark: (1) Our generalization bound for vanilla RNNs is significantly tighter than the best of existing results; (2) We are not aware of any other generalization bounds for MGU, LSTM, and Conv RNNs in the exiting literature; (3) We demonstrate the advantages of these variants in generalization.

ZO-AdaMM: Zeroth-Order Adaptive Momentum Method for Black-Box Optimization

The adaptive momentum method (AdaMM), which uses past gradients to update descent directions and learning rates simultaneously, has become one of the most popular first-order optimization methods for solving machine learning problems. However, AdaMM is not suited for solving black-box optimization problems, where explicit gradient forms are difficult or infeasible to obtain. In this paper, we propose a zeroth-order AdaMM (ZO-AdaMM) algorithm, that generalizes AdaMM to the gradient-free regime. We show that the convergence rate of ZO-AdaMM for both convex and nonconvex optimization is roughly a factor of $O(\sqrt{d})$ worse than that of the first-order AdaMM algorithm, where $d$ is problem size. In particular, we provide a deep understanding on why Mahalanobis distance matters in convergence of ZO-AdaMM and other AdaMM-type methods. As a byproduct, our analysis makes the first step toward understanding adaptive learning rate methods for nonconvex constrained optimization. Furthermore, we demonstrate two applications, designing per-image and universal adversarial attacks from black-box neural networks, respectively. We perform extensive experiments on ImageNet and empirically show that ZO-AdaMM converges much faster to a solution of high accuracy compared with $6$ state-of-the-art ZO optimization methods.

NOODL: Provable Online Dictionary Learning and Sparse Coding

We consider the dictionary learning problem, where the aim is to model the given data as a linear combination of a few columns of a matrix known as a dictionary, where the sparse weights forming the linear combination are known as coefficients. Since the dictionary and coefficients, parameterizing the linear model are unknown, the corresponding optimization is inherently non-convex. This was a major challenge until recently, when provable algorithms for dictionary learning were proposed. Yet, these provide guarantees only on the recovery of the dictionary, without explicit recovery guarantees on the coefficients. Moreover, any estimation error in the dictionary adversely impacts the ability to successfully localize and estimate the coefficients. This potentially limits the utility of existing provable dictionary learning methods in applications where coefficient recovery is of interest. To this end, we develop NOODL: a simple Neurally plausible alternating Optimization-based Online Dictionary Learning algorithm, which recovers both the dictionary and coefficients exactly at a geometric rate, when initialized appropriately. Our algorithm, NOODL, is also scalable and amenable for large scale distributed implementations in neural architectures, by which we mean that it only involves simple linear and non-linear operations. Finally, we corroborate these theoretical results via experimental evaluation of the proposed algorithm with the current state-of-the-art techniques.

Target-based Hyperspectral Demixing via Generalized Robust PCA

Localizing targets of interest in a given hyperspectral (HS) image has applications ranging from remote sensing to surveillance. This task of target detection leverages the fact that each material/object possesses its own characteristic spectral response, depending upon its composition. As $\textit{signatures}$ of different materials are often correlated, matched filtering based approaches may not be appropriate in this case. In this work, we present a technique to localize targets of interest based on their spectral signatures. We also present the corresponding recovery guarantees, leveraging our recent theoretical results. To this end, we model a HS image as a superposition of a low-rank component and a dictionary sparse component, wherein the dictionary consists of the $\textit{a priori}$ known characteristic spectral responses of the target we wish to localize. Finally, we analyze the performance of the proposed approach via experimental validation on real HS data for a classification task, and compare it with related techniques.