Early Directional Convergence in Deep Homogeneous Neural Networks for Small Initializations

This paper studies the gradient flow dynamics that arise when training deep homogeneous neural networks, starting with small initializations. The present work considers neural networks that are assumed to have locally Lipschitz gradients and an order of homogeneity strictly greater than two. This paper demonstrates that for sufficiently small initializations, during the early stages of training, the weights of the neural network remain small in norm and approximately converge in direction along the Karush-Kuhn-Tucker (KKT) points of the neural correlation function introduced in [1]. Additionally, for square loss and under a separability assumption on the weights of neural networks, a similar directional convergence of gradient flow dynamics is shown near certain saddle points of the loss function.

Directional Convergence Near Small Initializations and Saddles in Two-Homogeneous Neural Networks

This paper examines gradient flow dynamics of two-homogeneous neural networks for small initializations, where all weights are initialized near the origin. For both square and logistic losses, it is shown that for sufficiently small initializations, the gradient flow dynamics spend sufficient time in the neighborhood of the origin to allow the weights of the neural network to approximately converge in direction to the Karush-Kuhn-Tucker (KKT) points of a neural correlation function that quantifies the correlation between the output of the neural network and corresponding labels in the training data set. For square loss, it has been observed that neural networks undergo saddle-to-saddle dynamics when initialized close to the origin. Motivated by this, this paper also shows a similar directional convergence among weights of small magnitude in the neighborhood of certain saddle points.

Online Stochastic Gradient Descent Learns Linear Dynamical Systems from A Single Trajectory

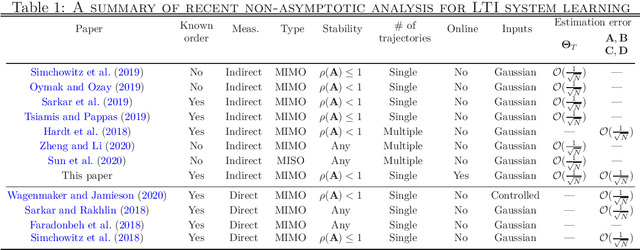
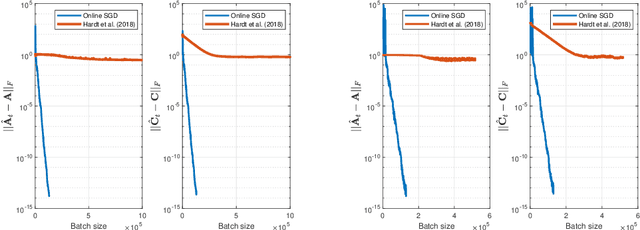
This work investigates the problem of estimating the weight matrices of a stable time-invariant linear dynamical system from a single sequence of noisy measurements. We show that if the unknown weight matrices describing the system are in Brunovsky canonical form, we can efficiently estimate the ground truth unknown matrices of the system from a linear system of equations formulated based on the transfer function of the system, using both online and offline stochastic gradient descent (SGD) methods. Specifically, by deriving concrete complexity bounds, we show that SGD converges linearly in expectation to any arbitrary small Frobenius norm distance from the ground truth weights. To the best of our knowledge, ours is the first work to establish linear convergence characteristics for online and offline gradient-based iterative methods for weight matrix estimation in linear dynamical systems from a single trajectory. Extensive numerical tests verify that the performance of the proposed methods is consistent with our theory, and show their superior performance relative to existing state of the art methods.

Convexifying Sparse Interpolation with Infinitely Wide Neural Networks: An Atomic Norm Approach

This work examines the problem of exact data interpolation via sparse (neuron count), infinitely wide, single hidden layer neural networks with leaky rectified linear unit activations. Using the atomic norm framework of [Chandrasekaran et al., 2012], we derive simple characterizations of the convex hulls of the corresponding atomic sets for this problem under several different constraints on the weights and biases of the network, thus obtaining equivalent convex formulations for these problems. A modest extension of our proposed framework to a binary classification problem is also presented. We explore the efficacy of the resulting formulations experimentally, and compare with networks trained via gradient descent.

Provable Online CP/PARAFAC Decomposition of a Structured Tensor via Dictionary Learning

We consider the problem of factorizing a structured 3-way tensor into its constituent Canonical Polyadic (CP) factors. This decomposition, which can be viewed as a generalization of singular value decomposition (SVD) for tensors, reveals how the tensor dimensions (features) interact with each other. However, since the factors are a priori unknown, the corresponding optimization problems are inherently non-convex. The existing guaranteed algorithms which handle this non-convexity incur an irreducible error (bias), and only apply to cases where all factors have the same structure. To this end, we develop a provable algorithm for online structured tensor factorization, wherein one of the factors obeys some incoherence conditions, and the others are sparse. Specifically we show that, under some relatively mild conditions on initialization, rank, and sparsity, our algorithm recovers the factors exactly (up to scaling and permutation) at a linear rate. Complementary to our theoretical results, our synthetic and real-world data evaluations showcase superior performance compared to related techniques. Moreover, its scalability and ability to learn on-the-fly makes it suitable for real-world tasks.

A Provably Communication-Efficient Asynchronous Distributed Inference Method for Convex and Nonconvex Problems

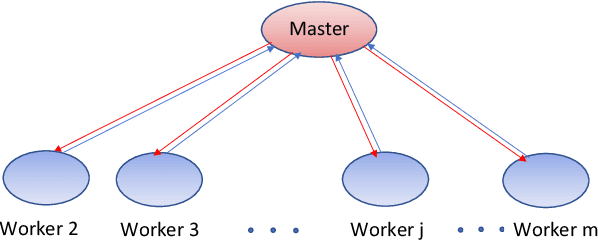
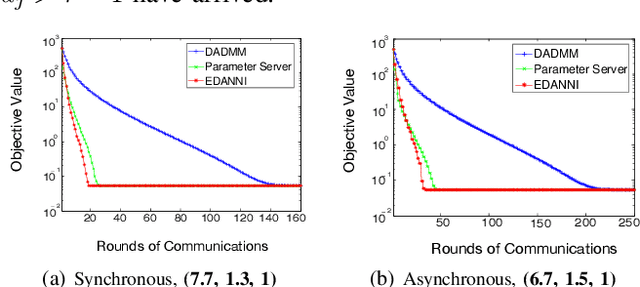
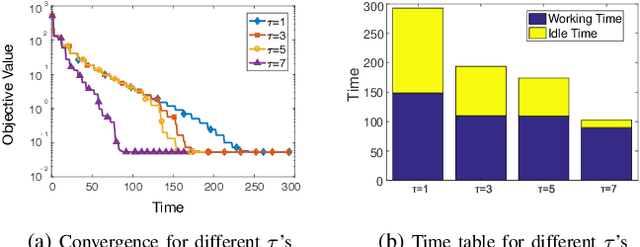
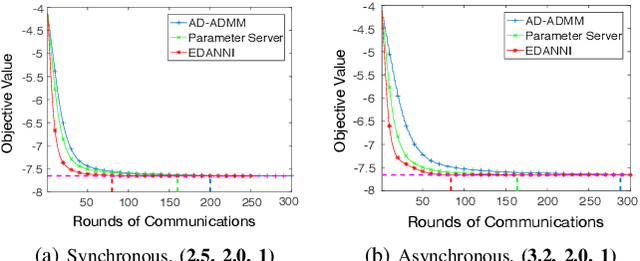
This paper proposes and analyzes a communication-efficient distributed optimization framework for general nonconvex nonsmooth signal processing and machine learning problems under an asynchronous protocol. At each iteration, worker machines compute gradients of a known empirical loss function using their own local data, and a master machine solves a related minimization problem to update the current estimate. We prove that for nonconvex nonsmooth problems, the proposed algorithm converges with a sublinear rate over the number of communication rounds, coinciding with the best theoretical rate that can be achieved for this class of problems. Linear convergence is established without any statistical assumptions of the local data for problems characterized by composite loss functions whose smooth parts are strongly convex. Extensive numerical experiments verify that the performance of the proposed approach indeed improves -- sometimes significantly -- over other state-of-the-art algorithms in terms of total communication efficiency.

NOODL: Provable Online Dictionary Learning and Sparse Coding

We consider the dictionary learning problem, where the aim is to model the given data as a linear combination of a few columns of a matrix known as a dictionary, where the sparse weights forming the linear combination are known as coefficients. Since the dictionary and coefficients, parameterizing the linear model are unknown, the corresponding optimization is inherently non-convex. This was a major challenge until recently, when provable algorithms for dictionary learning were proposed. Yet, these provide guarantees only on the recovery of the dictionary, without explicit recovery guarantees on the coefficients. Moreover, any estimation error in the dictionary adversely impacts the ability to successfully localize and estimate the coefficients. This potentially limits the utility of existing provable dictionary learning methods in applications where coefficient recovery is of interest. To this end, we develop NOODL: a simple Neurally plausible alternating Optimization-based Online Dictionary Learning algorithm, which recovers both the dictionary and coefficients exactly at a geometric rate, when initialized appropriately. Our algorithm, NOODL, is also scalable and amenable for large scale distributed implementations in neural architectures, by which we mean that it only involves simple linear and non-linear operations. Finally, we corroborate these theoretical results via experimental evaluation of the proposed algorithm with the current state-of-the-art techniques.

TensorMap: Lidar-Based Topological Mapping and Localization via Tensor Decompositions

We propose a technique to develop (and localize in) topological maps from light detection and ranging (Lidar) data. Localizing an autonomous vehicle with respect to a reference map in real-time is crucial for its safe operation. Owing to the rich information provided by Lidar sensors, these are emerging as a promising choice for this task. However, since a Lidar outputs a large amount of data every fraction of a second, it is progressively harder to process the information in real-time. Consequently, current systems have migrated towards faster alternatives at the expense of accuracy. To overcome this inherent trade-off between latency and accuracy, we propose a technique to develop topological maps from Lidar data using the orthogonal Tucker3 tensor decomposition. Our experimental evaluations demonstrate that in addition to achieving a high compression ratio as compared to full data, the proposed technique, $\textit{TensorMap}$, also accurately detects the position of the vehicle in a graph-based representation of a map. We also analyze the robustness of the proposed technique to Gaussian and translational noise, thus initiating explorations into potential applications of tensor decompositions in Lidar data analysis.

Target-based Hyperspectral Demixing via Generalized Robust PCA

Localizing targets of interest in a given hyperspectral (HS) image has applications ranging from remote sensing to surveillance. This task of target detection leverages the fact that each material/object possesses its own characteristic spectral response, depending upon its composition. As $\textit{signatures}$ of different materials are often correlated, matched filtering based approaches may not be appropriate in this case. In this work, we present a technique to localize targets of interest based on their spectral signatures. We also present the corresponding recovery guarantees, leveraging our recent theoretical results. To this end, we model a HS image as a superposition of a low-rank component and a dictionary sparse component, wherein the dictionary consists of the $\textit{a priori}$ known characteristic spectral responses of the target we wish to localize. Finally, we analyze the performance of the proposed approach via experimental validation on real HS data for a classification task, and compare it with related techniques.

A Dictionary-Based Generalization of Robust PCA Part II: Applications to Hyperspectral Demixing

We consider the task of localizing targets of interest in a hyperspectral (HS) image based on their spectral signature(s), by posing the problem as two distinct convex demixing task(s). With applications ranging from remote sensing to surveillance, this task of target detection leverages the fact that each material/object possesses its own characteristic spectral response, depending upon its composition. However, since $\textit{signatures}$ of different materials are often correlated, matched filtering-based approaches may not be apply here. To this end, we model a HS image as a superposition of a low-rank component and a dictionary sparse component, wherein the dictionary consists of the $\textit{a priori}$ known characteristic spectral responses of the target we wish to localize, and develop techniques for two different sparsity structures, resulting from different model assumptions. We also present the corresponding recovery guarantees, leveraging our recent theoretical results from a companion paper. Finally, we analyze the performance of the proposed approach via experimental evaluations on real HS datasets for a classification task, and compare its performance with related techniques.