Data-Driven Adaptive Network Slicing for Multi-Tenant Networks

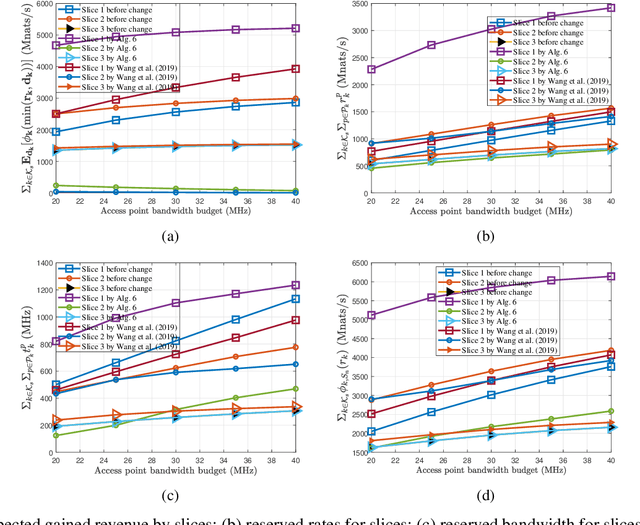
Network slicing to support multi-tenancy plays a key role in improving the performance of 5G networks. In this paper, we propose a two time-scale framework for the reservation-based network slicing in the backhaul and Radio Access Network (RAN). In the proposed two time-scale scheme, a subset of network slices is activated via a novel sparse optimization framework in the long time-scale with the goal of maximizing the expected utilities of tenants while in the short time-scale the activated slices are reconfigured according to the time-varying user traffic and channel states. Specifically, using the statistics from users and channels and also considering the expected utility from serving users of a slice and the reconfiguration cost, we formulate a sparse optimization problem to update the configuration of a slice resources such that the maximum isolation of reserved resources is enforced. The formulated optimization problems for long and short time-scales are non-convex and difficult to solve. We use the $\ell_q$-norm, $0<q<1$, and group LASSO regularizations to iteratively find convex approximations of the optimization problems. We propose a Frank-Wolfe algorithm to iteratively solve approximated problems in long time-scales. To cope with the dynamical nature of traffic variations, we propose a fast, distributed algorithm to solve the approximated optimization problems in short time-scales. Simulation results demonstrate the performance of our approaches relative to optimal solutions and the existing state of the art method.

Resource Reservation in Backhaul and Radio Access Network with Uncertain User Demands

Resource reservation is an essential step to enable wireless data networks to support a wide range of user demands. In this paper, we consider the problem of joint resource reservation in the backhaul and Radio Access Network (RAN) based on the statistics of user demands and channel states, and also network availability. The goal is to maximize the sum of expected traffic flow rates, subject to link and access point budget constraints, while minimizing the expected outage of downlinks. The formulated problem turns out to be non-convex and difficult to solve to global optimality. We propose an efficient Block Coordinate Descent (BCD) algorithm to approximately solve the problem. The proposed BCD algorithm optimizes the link capacity reservation in the backhaul using a novel multipath routing algorithm that decomposes the problem down to link-level and parallelizes the computation across backhaul links, while the reservation of transmission resources in RAN is carried out via a novel scalable and distributed algorithm based on Block Successive Upper-bound Minimization (BSUM). We prove that the proposed BCD algorithm converges to a Karush-Kuhn-Tucker solution. Simulation results verify the efficiency and the efficacy of our BCD approach against two heuristic algorithms.

Online Stochastic Gradient Descent Learns Linear Dynamical Systems from A Single Trajectory

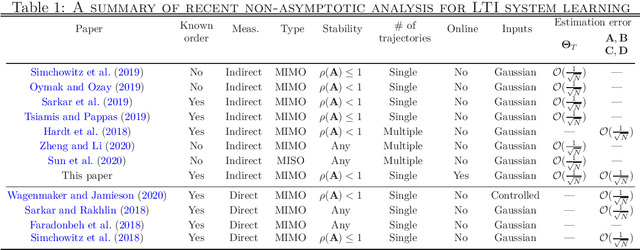
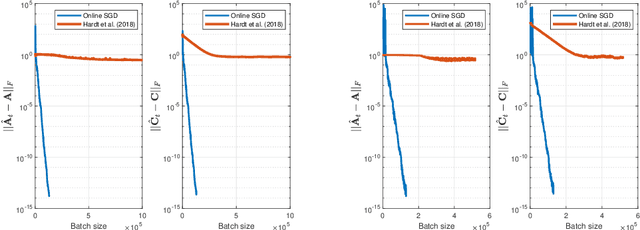
This work investigates the problem of estimating the weight matrices of a stable time-invariant linear dynamical system from a single sequence of noisy measurements. We show that if the unknown weight matrices describing the system are in Brunovsky canonical form, we can efficiently estimate the ground truth unknown matrices of the system from a linear system of equations formulated based on the transfer function of the system, using both online and offline stochastic gradient descent (SGD) methods. Specifically, by deriving concrete complexity bounds, we show that SGD converges linearly in expectation to any arbitrary small Frobenius norm distance from the ground truth weights. To the best of our knowledge, ours is the first work to establish linear convergence characteristics for online and offline gradient-based iterative methods for weight matrix estimation in linear dynamical systems from a single trajectory. Extensive numerical tests verify that the performance of the proposed methods is consistent with our theory, and show their superior performance relative to existing state of the art methods.