Online Stochastic Gradient Descent Learns Linear Dynamical Systems from A Single Trajectory
Paper and Code
Feb 23, 2021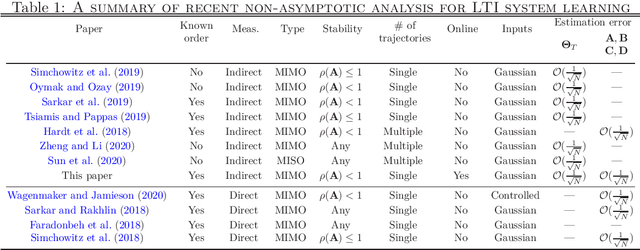

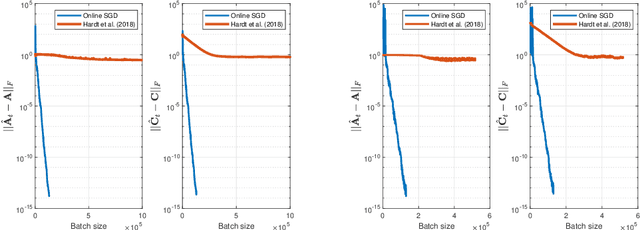

This work investigates the problem of estimating the weight matrices of a stable time-invariant linear dynamical system from a single sequence of noisy measurements. We show that if the unknown weight matrices describing the system are in Brunovsky canonical form, we can efficiently estimate the ground truth unknown matrices of the system from a linear system of equations formulated based on the transfer function of the system, using both online and offline stochastic gradient descent (SGD) methods. Specifically, by deriving concrete complexity bounds, we show that SGD converges linearly in expectation to any arbitrary small Frobenius norm distance from the ground truth weights. To the best of our knowledge, ours is the first work to establish linear convergence characteristics for online and offline gradient-based iterative methods for weight matrix estimation in linear dynamical systems from a single trajectory. Extensive numerical tests verify that the performance of the proposed methods is consistent with our theory, and show their superior performance relative to existing state of the art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge