A Provably Communication-Efficient Asynchronous Distributed Inference Method for Convex and Nonconvex Problems

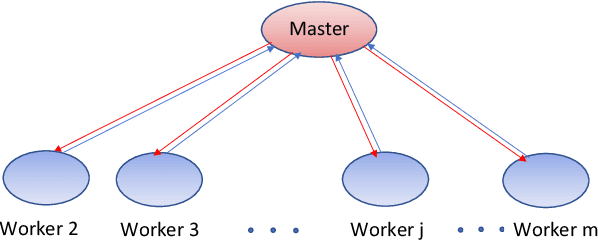
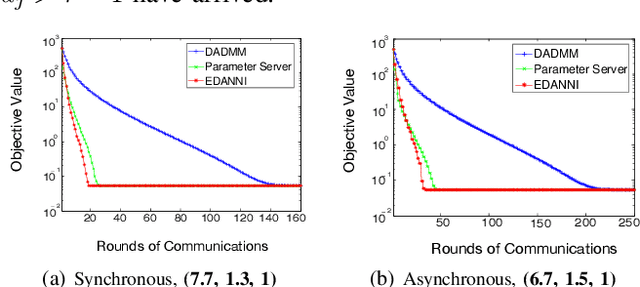
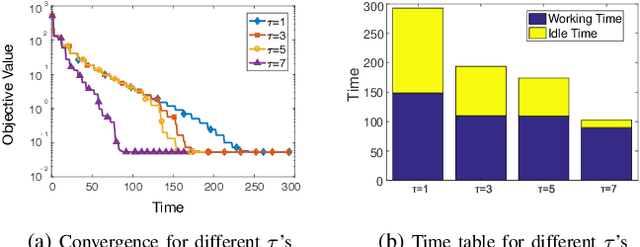
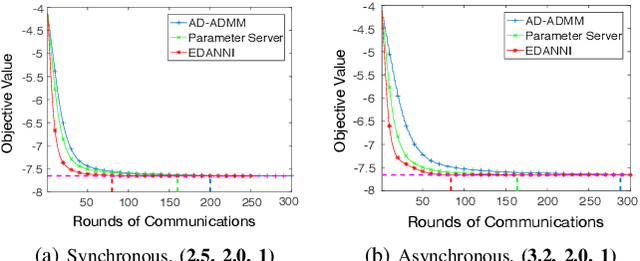
This paper proposes and analyzes a communication-efficient distributed optimization framework for general nonconvex nonsmooth signal processing and machine learning problems under an asynchronous protocol. At each iteration, worker machines compute gradients of a known empirical loss function using their own local data, and a master machine solves a related minimization problem to update the current estimate. We prove that for nonconvex nonsmooth problems, the proposed algorithm converges with a sublinear rate over the number of communication rounds, coinciding with the best theoretical rate that can be achieved for this class of problems. Linear convergence is established without any statistical assumptions of the local data for problems characterized by composite loss functions whose smooth parts are strongly convex. Extensive numerical experiments verify that the performance of the proposed approach indeed improves -- sometimes significantly -- over other state-of-the-art algorithms in terms of total communication efficiency.

A Dictionary-Based Generalization of Robust PCA Part II: Applications to Hyperspectral Demixing

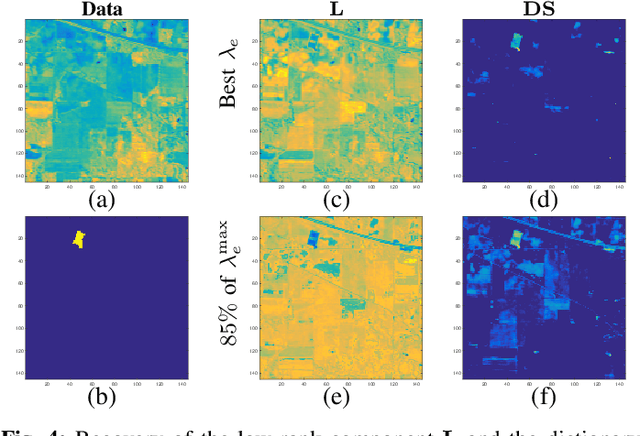
We consider the task of localizing targets of interest in a hyperspectral (HS) image based on their spectral signature(s), by posing the problem as two distinct convex demixing task(s). With applications ranging from remote sensing to surveillance, this task of target detection leverages the fact that each material/object possesses its own characteristic spectral response, depending upon its composition. However, since $\textit{signatures}$ of different materials are often correlated, matched filtering-based approaches may not be apply here. To this end, we model a HS image as a superposition of a low-rank component and a dictionary sparse component, wherein the dictionary consists of the $\textit{a priori}$ known characteristic spectral responses of the target we wish to localize, and develop techniques for two different sparsity structures, resulting from different model assumptions. We also present the corresponding recovery guarantees, leveraging our recent theoretical results from a companion paper. Finally, we analyze the performance of the proposed approach via experimental evaluations on real HS datasets for a classification task, and compare its performance with related techniques.

A Dictionary-Based Generalization of Robust PCA Part I: Study of Theoretical Properties

We consider the decomposition of a data matrix assumed to be a superposition of a low-rank matrix and a component which is sparse in a known dictionary, using a convex demixing method. We consider two sparsity structures for the sparse factor of the dictionary sparse component, namely entry-wise and column-wise sparsity, and provide a unified analysis, encompassing both undercomplete and the overcomplete dictionary cases, to show that the constituent matrices can be successfully recovered under some relatively mild conditions on incoherence, sparsity, and rank. We corroborate our theoretical results by presenting empirical evaluations in terms of phase transitions in rank and sparsity, in comparison to related techniques. Investigation of a specific application in hyperspectral imaging is included in an accompanying paper.