A Provably Communication-Efficient Asynchronous Distributed Inference Method for Convex and Nonconvex Problems
Paper and Code
Mar 16, 2019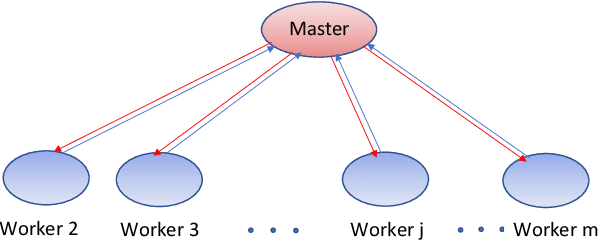
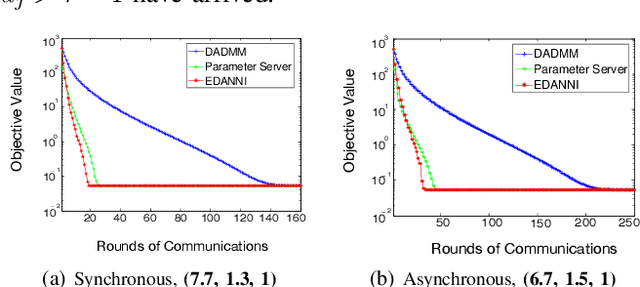
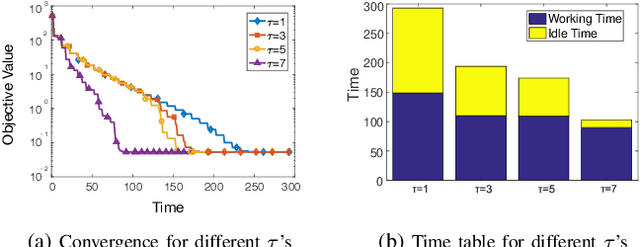
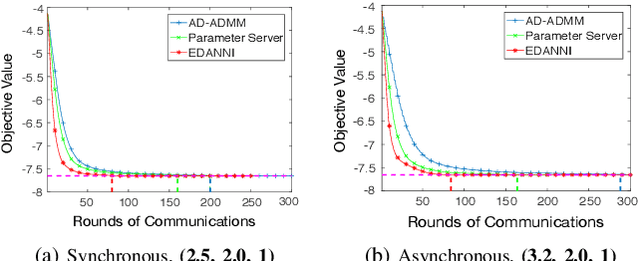
This paper proposes and analyzes a communication-efficient distributed optimization framework for general nonconvex nonsmooth signal processing and machine learning problems under an asynchronous protocol. At each iteration, worker machines compute gradients of a known empirical loss function using their own local data, and a master machine solves a related minimization problem to update the current estimate. We prove that for nonconvex nonsmooth problems, the proposed algorithm converges with a sublinear rate over the number of communication rounds, coinciding with the best theoretical rate that can be achieved for this class of problems. Linear convergence is established without any statistical assumptions of the local data for problems characterized by composite loss functions whose smooth parts are strongly convex. Extensive numerical experiments verify that the performance of the proposed approach indeed improves -- sometimes significantly -- over other state-of-the-art algorithms in terms of total communication efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge