Learning from Censored and Dependent Data: The case of Linear Dynamics

Observations from dynamical systems often exhibit irregularities, such as censoring, where values are recorded only if they fall within a certain range. Censoring is ubiquitous in practice, due to saturating sensors, limit-of-detection effects, and image-frame effects. In light of recent developments on learning linear dynamical systems (LDSs), and on censored statistics with independent data, we revisit the decades-old problem of learning an LDS, from censored observations (Lee and Maddala (1985); Zeger and Brookmeyer (1986)). Here, the learner observes the state $x_t \in \mathbb{R}^d$ if and only if $x_t$ belongs to some set $S_t \subseteq \mathbb{R}^d$. We develop the first computationally and statistically efficient algorithm for learning the system, assuming only oracle access to the sets $S_t$. Our algorithm, Stochastic Online Newton with Switching Gradients, is a novel second-order method that builds on the Online Newton Step (ONS) of Hazan et al. (2007). Our Switching-Gradient scheme does not always use (stochastic) gradients of the function we want to optimize, which we call "censor-aware" function. Instead, in each iteration, it performs a simple test to decide whether to use the censor-aware, or another "censor-oblivious" function, for getting a stochastic gradient. In our analysis, we consider a "generic" Online Newton method, which uses arbitrary vectors instead of gradients, and we prove an error-bound for it. This can be used to appropriately design these vectors, leading to our Switching-Gradient scheme. This framework significantly deviates from the recent long line of works on censored statistics (e.g., Daskalakis et al. (2018); Kontonis et al. (2019); Daskalakis et al. (2019)), which apply Stochastic Gradient Descent (SGD), and their analysis reduces to establishing conditions for off-the-shelf SGD-bounds.

Geometric Exploration for Online Control

We study the control of an \emph{unknown} linear dynamical system under general convex costs. The objective is minimizing regret vs. the class of disturbance-feedback-controllers, which encompasses all stabilizing linear-dynamical-controllers. In this work, we first consider the case of known cost functions, for which we design the first polynomial-time algorithm with $n^3\sqrt{T}$-regret, where $n$ is the dimension of the state plus the dimension of control input. The $\sqrt{T}$-horizon dependence is optimal, and improves upon the previous best known bound of $T^{2/3}$. The main component of our algorithm is a novel geometric exploration strategy: we adaptively construct a sequence of barycentric spanners in the policy space. Second, we consider the case of bandit feedback, for which we give the first polynomial-time algorithm with $poly(n)\sqrt{T}$-regret, building on Stochastic Bandit Convex Optimization.

Over-parameterized Adversarial Training: An Analysis Overcoming the Curse of Dimensionality

Adversarial training is a popular method to give neural nets robustness against adversarial perturbations. In practice adversarial training leads to low robust training loss. However, a rigorous explanation for why this happens under natural conditions is still missing. Recently a convergence theory for standard (non-adversarial) supervised training was developed by various groups for {\em very overparametrized} nets. It is unclear how to extend these results to adversarial training because of the min-max objective. Recently, a first step towards this direction was made by Gao et al. using tools from online learning, but they require the width of the net to be \emph{exponential} in input dimension $d$, and with an unnatural activation function. Our work proves convergence to low robust training loss for \emph{polynomial} width instead of exponential, under natural assumptions and with the ReLU activation. Key element of our proof is showing that ReLU networks near initialization can approximate the step function, which may be of independent interest.

A Theoretical Analysis of Contrastive Unsupervised Representation Learning

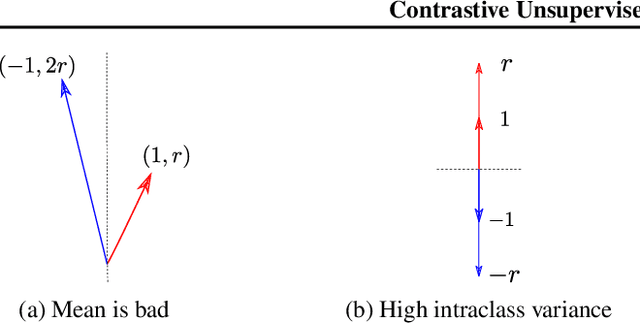
Recent empirical works have successfully used unlabeled data to learn feature representations that are broadly useful in downstream classification tasks. Several of these methods are reminiscent of the well-known word2vec embedding algorithm: leveraging availability of pairs of semantically "similar" data points and "negative samples," the learner forces the inner product of representations of similar pairs with each other to be higher on average than with negative samples. The current paper uses the term contrastive learning for such algorithms and presents a theoretical framework for analyzing them by introducing latent classes and hypothesizing that semantically similar points are sampled from the same latent class. This framework allows us to show provable guarantees on the performance of the learned representations on the average classification task that is comprised of a subset of the same set of latent classes. Our generalization bound also shows that learned representations can reduce (labeled) sample complexity on downstream tasks. We conduct controlled experiments in both the text and image domains to support the theory.