LLMs Need Encoders for Semantic IDs Too

Multimodal LLMs use dedicated encoders to bridge non-language modalities (vision encoders for images, depth models for audio codec tokens) because raw token embeddings alone cannot capture modality-specific structure. We argue that Semantic IDs (SIDs), the hierarchical codes used in generative recommendation, constitute another such modality: a SID level token's meaning depends on its prefix context, yet current systems simply add SID tokens to the vocabulary and rely on training to learn these context-dependent meanings from scratch. We propose PrefixMem, a lightweight SID encoder based on prefix n-gram memory tables that provides the LLM with structured, prefix-conditioned representations at SID token positions. Like vision encoders in multimodal LLMs, PrefixMem can be pre-trained independently and then attached to any LLM for joint training. We evaluate on large-scale data from Pinterest across multiple LLM families and show that PrefixMem improves deepest-level SID accuracy by up to 46% relative and full-SID retrieval recall by up to 22% relative at matched training compute. The encoder's benefit concentrates on hard examples where greedy decoding fails, with up to 77% relative accuracy gains, confirming that SID tokens benefit from a dedicated encoder just as other non-language modalities do.

Privacy Preserving Conversion Modeling in Data Clean Room

In the realm of online advertising, accurately predicting the conversion rate (CVR) is crucial for enhancing advertising efficiency and user satisfaction. This paper addresses the challenge of CVR prediction while adhering to user privacy preferences and advertiser requirements. Traditional methods face obstacles such as the reluctance of advertisers to share sensitive conversion data and the limitations of model training in secure environments like data clean rooms. We propose a novel model training framework that enables collaborative model training without sharing sample-level gradients with the advertising platform. Our approach introduces several innovative components: (1) utilizing batch-level aggregated gradients instead of sample-level gradients to minimize privacy risks; (2) applying adapter-based parameter-efficient fine-tuning and gradient compression to reduce communication costs; and (3) employing de-biasing techniques to train the model under label differential privacy, thereby maintaining accuracy despite privacy-enhanced label perturbations. Our experimental results, conducted on industrial datasets, demonstrate that our method achieves competitive ROCAUC performance while significantly decreasing communication overhead and complying with both advertiser privacy requirements and user privacy choices. This framework establishes a new standard for privacy-preserving, high-performance CVR prediction in the digital advertising landscape.

Face De-identification: State-of-the-art Methods and Comparative Studies

The widespread use of image acquisition technologies, along with advances in facial recognition, has raised serious privacy concerns. Face de-identification usually refers to the process of concealing or replacing personal identifiers, which is regarded as an effective means to protect the privacy of facial images. A significant number of methods for face de-identification have been proposed in recent years. In this survey, we provide a comprehensive review of state-of-the-art face de-identification methods, categorized into three levels: pixel-level, representation-level, and semantic-level techniques. We systematically evaluate these methods based on two key criteria, the effectiveness of privacy protection and preservation of image utility, highlighting their advantages and limitations. Our analysis includes qualitative and quantitative comparisons of the main algorithms, demonstrating that deep learning-based approaches, particularly those using Generative Adversarial Networks (GANs) and diffusion models, have achieved significant advancements in balancing privacy and utility. Experimental results reveal that while recent methods demonstrate strong privacy protection, trade-offs remain in visual fidelity and computational complexity. This survey not only summarizes the current landscape but also identifies key challenges and future research directions in face de-identification.

Face Aging via Diffusion-based Editing

In this paper, we address the problem of face aging: generating past or future facial images by incorporating age-related changes to the given face. Previous aging methods rely solely on human facial image datasets and are thus constrained by their inherent scale and bias. This restricts their application to a limited generatable age range and the inability to handle large age gaps. We propose FADING, a novel approach to address Face Aging via DIffusion-based editiNG. We go beyond existing methods by leveraging the rich prior of large-scale language-image diffusion models. First, we specialize a pre-trained diffusion model for the task of face age editing by using an age-aware fine-tuning scheme. Next, we invert the input image to latent noise and obtain optimized null text embeddings. Finally, we perform text-guided local age editing via attention control. The quantitative and qualitative analyses demonstrate that our method outperforms existing approaches with respect to aging accuracy, attribute preservation, and aging quality.

Distributed Adversarial Training to Robustify Deep Neural Networks at Scale

Current deep neural networks (DNNs) are vulnerable to adversarial attacks, where adversarial perturbations to the inputs can change or manipulate classification. To defend against such attacks, an effective and popular approach, known as adversarial training (AT), has been shown to mitigate the negative impact of adversarial attacks by virtue of a min-max robust training method. While effective, it remains unclear whether it can successfully be adapted to the distributed learning context. The power of distributed optimization over multiple machines enables us to scale up robust training over large models and datasets. Spurred by that, we propose distributed adversarial training (DAT), a large-batch adversarial training framework implemented over multiple machines. We show that DAT is general, which supports training over labeled and unlabeled data, multiple types of attack generation methods, and gradient compression operations favored for distributed optimization. Theoretically, we provide, under standard conditions in the optimization theory, the convergence rate of DAT to the first-order stationary points in general non-convex settings. Empirically, we demonstrate that DAT either matches or outperforms state-of-the-art robust accuracies and achieves a graceful training speedup (e.g., on ResNet-50 under ImageNet). Codes are available at https://github.com/dat-2022/dat.

Toward Communication Efficient Adaptive Gradient Method

In recent years, distributed optimization is proven to be an effective approach to accelerate training of large scale machine learning models such as deep neural networks. With the increasing computation power of GPUs, the bottleneck of training speed in distributed training is gradually shifting from computation to communication. Meanwhile, in the hope of training machine learning models on mobile devices, a new distributed training paradigm called ``federated learning'' has become popular. The communication time in federated learning is especially important due to the low bandwidth of mobile devices. While various approaches to improve the communication efficiency have been proposed for federated learning, most of them are designed with SGD as the prototype training algorithm. While adaptive gradient methods have been proven effective for training neural nets, the study of adaptive gradient methods in federated learning is scarce. In this paper, we propose an adaptive gradient method that can guarantee both the convergence and the communication efficiency for federated learning.

On the Convergence of Decentralized Adaptive Gradient Methods

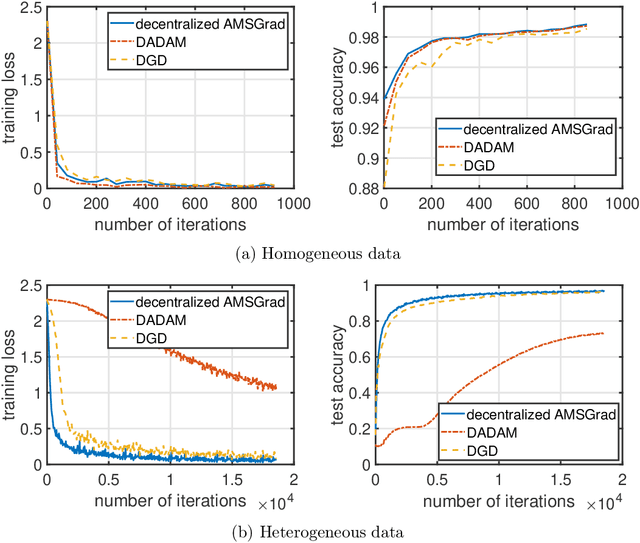
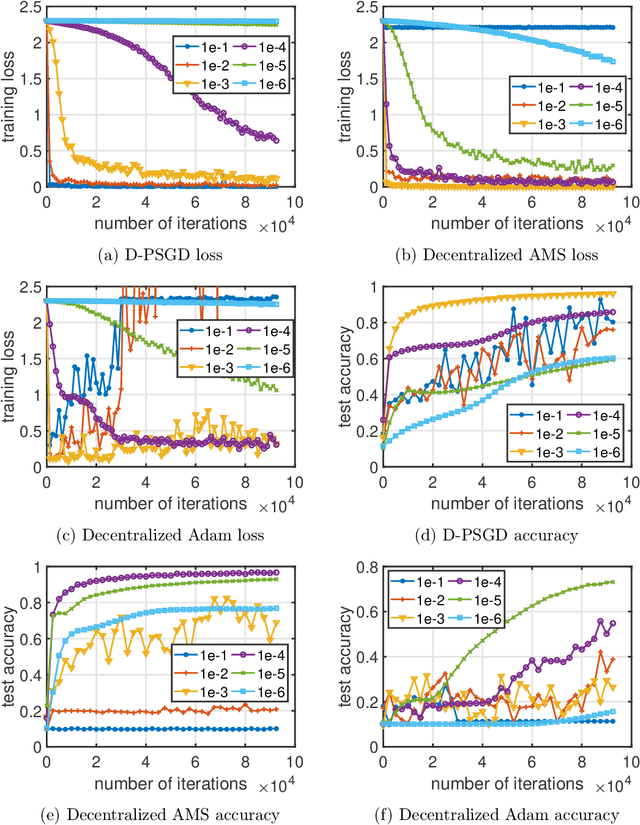
Adaptive gradient methods including Adam, AdaGrad, and their variants have been very successful for training deep learning models, such as neural networks. Meanwhile, given the need for distributed computing, distributed optimization algorithms are rapidly becoming a focal point. With the growth of computing power and the need for using machine learning models on mobile devices, the communication cost of distributed training algorithms needs careful consideration. In this paper, we introduce novel convergent decentralized adaptive gradient methods and rigorously incorporate adaptive gradient methods into decentralized training procedures. Specifically, we propose a general algorithmic framework that can convert existing adaptive gradient methods to their decentralized counterparts. In addition, we thoroughly analyze the convergence behavior of the proposed algorithmic framework and show that if a given adaptive gradient method converges, under some specific conditions, then its decentralized counterpart is also convergent. We illustrate the benefit of our generic decentralized framework on a prototype method, i.e., AMSGrad, both theoretically and numerically.

Understanding Clipping for Federated Learning: Convergence and Client-Level Differential Privacy

Providing privacy protection has been one of the primary motivations of Federated Learning (FL). Recently, there has been a line of work on incorporating the formal privacy notion of differential privacy with FL. To guarantee the client-level differential privacy in FL algorithms, the clients' transmitted model updates have to be clipped before adding privacy noise. Such clipping operation is substantially different from its counterpart of gradient clipping in the centralized differentially private SGD and has not been well-understood. In this paper, we first empirically demonstrate that the clipped FedAvg can perform surprisingly well even with substantial data heterogeneity when training neural networks, which is partly because the clients' updates become similar for several popular deep architectures. Based on this key observation, we provide the convergence analysis of a differential private (DP) FedAvg algorithm and highlight the relationship between clipping bias and the distribution of the clients' updates. To the best of our knowledge, this is the first work that rigorously investigates theoretical and empirical issues regarding the clipping operation in FL algorithms.

Understanding Gradient Clipping in Private SGD: A Geometric Perspective

Deep learning models are increasingly popular in many machine learning applications where the training data may contain sensitive information. To provide formal and rigorous privacy guarantee, many learning systems now incorporate differential privacy by training their models with (differentially) private SGD. A key step in each private SGD update is gradient clipping that shrinks the gradient of an individual example whenever its L2 norm exceeds some threshold. We first demonstrate how gradient clipping can prevent SGD from converging to stationary point. We then provide a theoretical analysis that fully quantifies the clipping bias on convergence with a disparity measure between the gradient distribution and a geometrically symmetric distribution. Our empirical evaluation further suggests that the gradient distributions along the trajectory of private SGD indeed exhibit symmetric structure that favors convergence. Together, our results provide an explanation why private SGD with gradient clipping remains effective in practice despite its potential clipping bias. Finally, we develop a new perturbation-based technique that can provably correct the clipping bias even for instances with highly asymmetric gradient distributions.

Private Stochastic Non-Convex Optimization: Adaptive Algorithms and Tighter Generalization Bounds

We study differentially private (DP) algorithms for stochastic non-convex optimization. In this problem, the goal is to minimize the population loss over a $p$-dimensional space given $n$ i.i.d. samples drawn from a distribution. We improve upon the population gradient bound of ${\sqrt{p}}/{\sqrt{n}}$ from prior work and obtain a sharper rate of $\sqrt[4]{p}/\sqrt{n}$. We obtain this rate by providing the first analyses on a collection of private gradient-based methods, including adaptive algorithms DP RMSProp and DP Adam. Our proof technique leverages the connection between differential privacy and adaptive data analysis to bound gradient estimation error at every iterate, which circumvents the worse generalization bound from the standard uniform convergence argument. Finally, we evaluate the proposed algorithms on two popular deep learning tasks and demonstrate the empirical advantages of DP adaptive gradient methods over standard DP SGD.