Conservative Contextual Bandits: Beyond Linear Representations

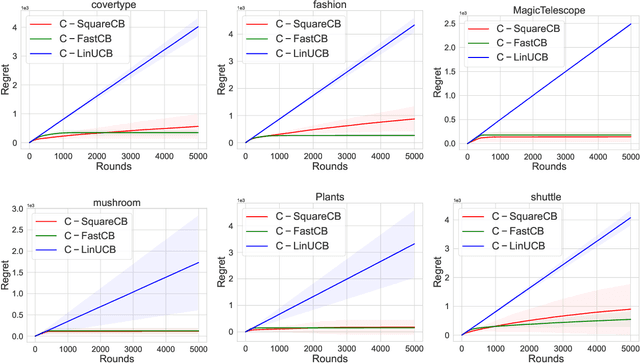
Conservative Contextual Bandits (CCBs) address safety in sequential decision making by requiring that an agent's policy, along with minimizing regret, also satisfies a safety constraint: the performance is not worse than a baseline policy (e.g., the policy that the company has in production) by more than $(1+\alpha)$ factor. Prior work developed UCB-style algorithms in the multi-armed [Wu et al., 2016] and contextual linear [Kazerouni et al., 2017] settings. However, in practice the cost of the arms is often a non-linear function, and therefore existing UCB algorithms are ineffective in such settings. In this paper, we consider CCBs beyond the linear case and develop two algorithms $\mathtt{C-SquareCB}$ and $\mathtt{C-FastCB}$, using Inverse Gap Weighting (IGW) based exploration and an online regression oracle. We show that the safety constraint is satisfied with high probability and that the regret of $\mathtt{C-SquareCB}$ is sub-linear in horizon $T$, while the regret of $\mathtt{C-FastCB}$ is first-order and is sub-linear in $L^*$, the cumulative loss of the optimal policy. Subsequently, we use a neural network for function approximation and online gradient descent as the regression oracle to provide $\tilde{O}(\sqrt{KT} + K/\alpha) $ and $\tilde{O}(\sqrt{KL^*} + K (1 + 1/\alpha))$ regret bounds, respectively. Finally, we demonstrate the efficacy of our algorithms on real-world data and show that they significantly outperform the existing baseline while maintaining the performance guarantee.

Sketched Adaptive Federated Deep Learning: A Sharp Convergence Analysis

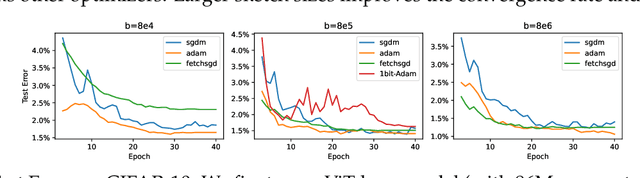
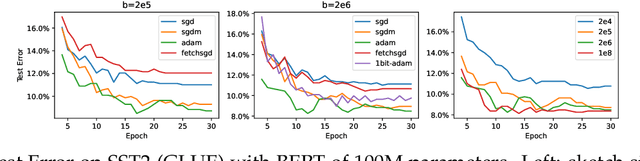
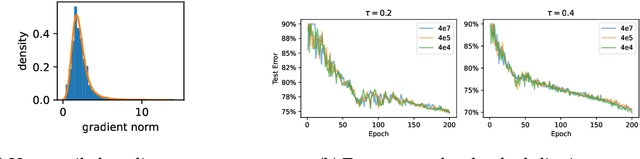
Combining gradient compression methods (e.g., CountSketch, quantization) and adaptive optimizers (e.g., Adam, AMSGrad) is a desirable goal in federated learning (FL), with potential benefits on both fewer communication rounds and less per-round communication. In spite of the preliminary empirical success of sketched adaptive methods, existing convergence analyses show the communication cost to have a linear dependence on the ambient dimension, i.e., number of parameters, which is prohibitively high for modern deep learning models. In this work, we introduce specific sketched adaptive federated learning (SAFL) algorithms and, as our main contribution, provide theoretical convergence analyses in different FL settings with guarantees on communication cost depending only logarithmically (instead of linearly) on the ambient dimension. Unlike existing analyses, we show that the entry-wise sketching noise existent in the preconditioners and the first moments of SAFL can be implicitly addressed by leveraging the recently-popularized anisotropic curvatures in deep learning losses, e.g., fast decaying loss Hessian eigen-values. In the i.i.d. client setting of FL, we show that SAFL achieves asymptotic $O(1/\sqrt{T})$ convergence, and converges faster in the initial epochs. In the non-i.i.d. client setting, where non-adaptive methods lack convergence guarantees, we show that SACFL (SAFL with clipping) algorithms can provably converge in spite of the additional heavy-tailed noise. Our theoretical claims are supported by empirical studies on vision and language tasks, and in both fine-tuning and training-from-scratch regimes. Surprisingly, as a by-product of our analysis, the proposed SAFL methods are competitive with the state-of-the-art communication-efficient federated learning algorithms based on error feedback.

On the Generalizability of Foundation Models for Crop Type Mapping

Foundation models pre-trained using self-supervised and weakly-supervised learning have shown powerful transfer learning capabilities on various downstream tasks, including language understanding, text generation, and image recognition. Recently, the Earth observation (EO) field has produced several foundation models pre-trained directly on multispectral satellite imagery (e.g., Sentinel-2) for applications like precision agriculture, wildfire and drought monitoring, and natural disaster response. However, few studies have investigated the ability of these models to generalize to new geographic locations, and potential concerns of geospatial bias -- models trained on data-rich developed countries not transferring well to data-scarce developing countries -- remain. We investigate the ability of popular EO foundation models to transfer to new geographic regions in the agricultural domain, where differences in farming practices and class imbalance make transfer learning particularly challenging. We first select six crop classification datasets across five continents, normalizing for dataset size and harmonizing classes to focus on four major cereal grains: maize, soybean, rice, and wheat. We then compare three popular foundation models, pre-trained on SSL4EO-S12, SatlasPretrain, and ImageNet, using in-distribution (ID) and out-of-distribution (OOD) evaluation. Experiments show that pre-trained weights designed explicitly for Sentinel-2, such as SSL4EO-S12, outperform general pre-trained weights like ImageNet. Furthermore, the benefits of pre-training on OOD data are the most significant when only 10--100 ID training samples are used. Transfer learning and pre-training with OOD and limited ID data show promising applications, as many developing regions have scarce crop type labels. All harmonized datasets and experimental code are open-source and available for download.

Optimization and Generalization Guarantees for Weight Normalization

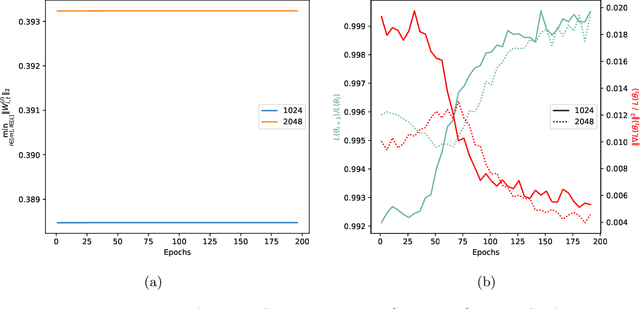
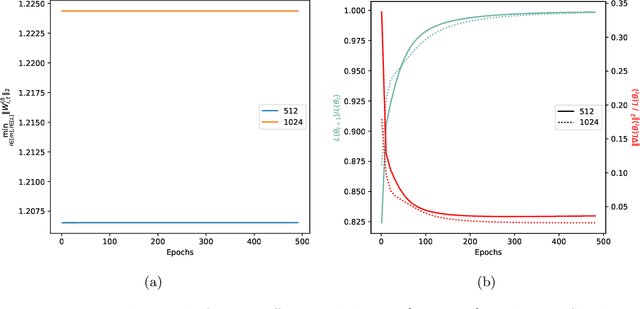
Weight normalization (WeightNorm) is widely used in practice for the training of deep neural networks and modern deep learning libraries have built-in implementations of it. In this paper, we provide the first theoretical characterizations of both optimization and generalization of deep WeightNorm models with smooth activation functions. For optimization, from the form of the Hessian of the loss, we note that a small Hessian of the predictor leads to a tractable analysis. Thus, we bound the spectral norm of the Hessian of WeightNorm networks and show its dependence on the network width and weight normalization terms--the latter being unique to networks without WeightNorm. Then, we use this bound to establish training convergence guarantees under suitable assumptions for gradient decent. For generalization, we use WeightNorm to get a uniform convergence based generalization bound, which is independent from the width and depends sublinearly on the depth. Finally, we present experimental results which illustrate how the normalization terms and other quantities of theoretical interest relate to the training of WeightNorm networks.

Loss Gradient Gaussian Width based Generalization and Optimization Guarantees

Generalization and optimization guarantees on the population loss in machine learning often rely on uniform convergence based analysis, typically based on the Rademacher complexity of the predictors. The rich representation power of modern models has led to concerns about this approach. In this paper, we present generalization and optimization guarantees in terms of the complexity of the gradients, as measured by the Loss Gradient Gaussian Width (LGGW). First, we introduce generalization guarantees directly in terms of the LGGW under a flexible gradient domination condition, which we demonstrate to hold empirically for deep models. Second, we show that sample reuse in finite sum (stochastic) optimization does not make the empirical gradient deviate from the population gradient as long as the LGGW is small. Third, focusing on deep networks, we present results showing how to bound their LGGW under mild assumptions. In particular, we show that their LGGW can be bounded (a) by the $L_2$-norm of the loss Hessian eigenvalues, which has been empirically shown to be $\tilde{O}(1)$ for commonly used deep models; and (b) in terms of the Gaussian width of the featurizer, i.e., the output of the last-but-one layer. To our knowledge, our generalization and optimization guarantees in terms of LGGW are the first results of its kind, avoid the pitfalls of predictor Rademacher complexity based analysis, and hold considerable promise towards quantitatively tight bounds for deep models.

Contextual Bandits with Online Neural Regression

Recent works have shown a reduction from contextual bandits to online regression under a realizability assumption [Foster and Rakhlin, 2020, Foster and Krishnamurthy, 2021]. In this work, we investigate the use of neural networks for such online regression and associated Neural Contextual Bandits (NeuCBs). Using existing results for wide networks, one can readily show a ${\mathcal{O}}(\sqrt{T})$ regret for online regression with square loss, which via the reduction implies a ${\mathcal{O}}(\sqrt{K} T^{3/4})$ regret for NeuCBs. Departing from this standard approach, we first show a $\mathcal{O}(\log T)$ regret for online regression with almost convex losses that satisfy QG (Quadratic Growth) condition, a generalization of the PL (Polyak-\L ojasiewicz) condition, and that have a unique minima. Although not directly applicable to wide networks since they do not have unique minima, we show that adding a suitable small random perturbation to the network predictions surprisingly makes the loss satisfy QG with unique minima. Based on such a perturbed prediction, we show a ${\mathcal{O}}(\log T)$ regret for online regression with both squared loss and KL loss, and subsequently convert these respectively to $\tilde{\mathcal{O}}(\sqrt{KT})$ and $\tilde{\mathcal{O}}(\sqrt{KL^*} + K)$ regret for NeuCB, where $L^*$ is the loss of the best policy. Separately, we also show that existing regret bounds for NeuCBs are $\Omega(T)$ or assume i.i.d. contexts, unlike this work. Finally, our experimental results on various datasets demonstrate that our algorithms, especially the one based on KL loss, persistently outperform existing algorithms.

AmbientFlow: Invertible generative models from incomplete, noisy measurements

Generative models have gained popularity for their potential applications in imaging science, such as image reconstruction, posterior sampling and data sharing. Flow-based generative models are particularly attractive due to their ability to tractably provide exact density estimates along with fast, inexpensive and diverse samples. Training such models, however, requires a large, high quality dataset of objects. In applications such as computed imaging, it is often difficult to acquire such data due to requirements such as long acquisition time or high radiation dose, while acquiring noisy or partially observed measurements of these objects is more feasible. In this work, we propose AmbientFlow, a framework for learning flow-based generative models directly from noisy and incomplete data. Using variational Bayesian methods, a novel framework for establishing flow-based generative models from noisy, incomplete data is proposed. Extensive numerical studies demonstrate the effectiveness of AmbientFlow in correctly learning the object distribution. The utility of AmbientFlow in a downstream inference task of image reconstruction is demonstrated.

SSL4EO-L: Datasets and Foundation Models for Landsat Imagery

The Landsat program is the longest-running Earth observation program in history, with 50+ years of data acquisition by 8 satellites. The multispectral imagery captured by sensors onboard these satellites is critical for a wide range of scientific fields. Despite the increasing popularity of deep learning and remote sensing, the majority of researchers still use decision trees and random forests for Landsat image analysis due to the prevalence of small labeled datasets and lack of foundation models. In this paper, we introduce SSL4EO-L, the first ever dataset designed for Self-Supervised Learning for Earth Observation for the Landsat family of satellites (including 3 sensors and 2 product levels) and the largest Landsat dataset in history (5M image patches). Additionally, we modernize and re-release the L7 Irish and L8 Biome cloud detection datasets, and introduce the first ML benchmark datasets for Landsats 4-5 TM and Landsat 7 ETM+ SR. Finally, we pre-train the first foundation models for Landsat imagery using SSL4EO-L and evaluate their performance on multiple semantic segmentation tasks. All datasets and model weights are available via the TorchGeo (https://github.com/microsoft/torchgeo) library, making reproducibility and experimentation easy, and enabling scientific advancements in the burgeoning field of remote sensing for a myriad of downstream applications.

Neural Exploitation and Exploration of Contextual Bandits

In this paper, we study utilizing neural networks for the exploitation and exploration of contextual multi-armed bandits. Contextual multi-armed bandits have been studied for decades with various applications. To solve the exploitation-exploration trade-off in bandits, there are three main techniques: epsilon-greedy, Thompson Sampling (TS), and Upper Confidence Bound (UCB). In recent literature, a series of neural bandit algorithms have been proposed to adapt to the non-linear reward function, combined with TS or UCB strategies for exploration. In this paper, instead of calculating a large-deviation based statistical bound for exploration like previous methods, we propose, ``EE-Net,'' a novel neural-based exploitation and exploration strategy. In addition to using a neural network (Exploitation network) to learn the reward function, EE-Net uses another neural network (Exploration network) to adaptively learn the potential gains compared to the currently estimated reward for exploration. We provide an instance-based $\widetilde{\mathcal{O}}(\sqrt{T})$ regret upper bound for EE-Net and show that EE-Net outperforms related linear and neural contextual bandit baselines on real-world datasets.

Alternate Loss Functions Can Improve the Performance of Artificial Neural Networks

All machine learning algorithms use a loss, cost, utility or reward function to encode the learning objective and oversee the learning process. This function that supervises learning is a frequently unrecognized hyperparameter that determines how incorrect outputs are penalized and can be tuned to improve performance. This paper shows that training speed and final accuracy of neural networks can significantly depend on the loss function used to train neural networks. In particular derivative values can be significantly different with different loss functions leading to significantly different performance after gradient descent based Backpropagation (BP) training. This paper explores the effect on performance of new loss functions that are more liberal or strict compared to the popular Cross-entropy loss in penalizing incorrect outputs. Eight new loss functions are proposed and a comparison of performance with different loss functions is presented. The new loss functions presented in this paper are shown to outperform Cross-entropy loss on computer vision and NLP benchmarks.