Principal-Agent Multitasking: the Uniformity of Optimal Contracts and its Efficient Learning via Instrumental Regression

This work studies the multitasking principal-agent problem. I first show a ``uniformity'' result. Specifically, when the tasks are perfect substitutes, and the agent's cost function is homogeneous to a certain degree, then the optimal contract only depends on the marginal utility of each task and the degree of homogeneity. I then study a setting where the marginal utility of each task is unknown so that the optimal contract must be learned or estimated with observational data. I identify this problem as a regression problem with measurement errors and observe that this problem can be cast as an instrumental regression problem. The current works observe that both the contract and the repeated observations (when available) can act as valid instrumental variables, and propose using the generalized method of moments estimator to compute an approximately optimal contract from offline data. I also study an online setting and show how the optimal contract can be efficiently learned in an online fashion using the two estimators. Here the principal faces an exploration-exploitation tradeoff: she must experiment with new contracts and observe their outcome whilst at the same time ensuring her experimentations are not deviating too much from the optimal contract. This work shows when repeated observations are available and agents are sufficiently ``diverse", the principal can achieve a very low $\widetilde{O}(d)$ cumulative utility loss, even with a ``pure exploitation" algorithm.

New Perspectives in Online Contract Design: Heterogeneous, Homogeneous, Non-myopic Agents and Team Production

This work studies the repeated principal-agent problem from an online learning perspective. The principal's goal is to learn the optimal contract that maximizes her utility through repeated interactions, without prior knowledge of the agent's type (i.e., the agent's cost and production functions). I study three different settings when the principal contracts with a $\textit{single}$ agent each round: 1. The agents are heterogeneous; 2. the agents are homogenous; 3. the principal interacts with the same agent and the agent is non-myopic. I present different approaches and techniques for designing learning algorithms in each setting. For heterogeneous agent types, I identify a condition that allows the problem to be reduced to Lipschitz bandits directly. For identical agents, I give a polynomial sample complexity scheme to learn the optimal contract based on inverse game theory. For strategic non-myopic agents, I design a low strategic-regret mechanism. Also, I identify a connection between linear contracts and posted-price auctions, showing the two can be reduced to one another, and give a regret lower bound on learning the optimal linear contract based on this observation. I also study a $\textit{team production}$ model. I identify a condition under which the principal's learning problem can be reformulated as solving a family of convex programs, thereby showing the optimal contract can be found efficiently.

Contextual Bandits with Online Neural Regression

Recent works have shown a reduction from contextual bandits to online regression under a realizability assumption [Foster and Rakhlin, 2020, Foster and Krishnamurthy, 2021]. In this work, we investigate the use of neural networks for such online regression and associated Neural Contextual Bandits (NeuCBs). Using existing results for wide networks, one can readily show a ${\mathcal{O}}(\sqrt{T})$ regret for online regression with square loss, which via the reduction implies a ${\mathcal{O}}(\sqrt{K} T^{3/4})$ regret for NeuCBs. Departing from this standard approach, we first show a $\mathcal{O}(\log T)$ regret for online regression with almost convex losses that satisfy QG (Quadratic Growth) condition, a generalization of the PL (Polyak-\L ojasiewicz) condition, and that have a unique minima. Although not directly applicable to wide networks since they do not have unique minima, we show that adding a suitable small random perturbation to the network predictions surprisingly makes the loss satisfy QG with unique minima. Based on such a perturbed prediction, we show a ${\mathcal{O}}(\log T)$ regret for online regression with both squared loss and KL loss, and subsequently convert these respectively to $\tilde{\mathcal{O}}(\sqrt{KT})$ and $\tilde{\mathcal{O}}(\sqrt{KL^*} + K)$ regret for NeuCB, where $L^*$ is the loss of the best policy. Separately, we also show that existing regret bounds for NeuCBs are $\Omega(T)$ or assume i.i.d. contexts, unlike this work. Finally, our experimental results on various datasets demonstrate that our algorithms, especially the one based on KL loss, persistently outperform existing algorithms.

Corruption-Robust Lipschitz Contextual Search

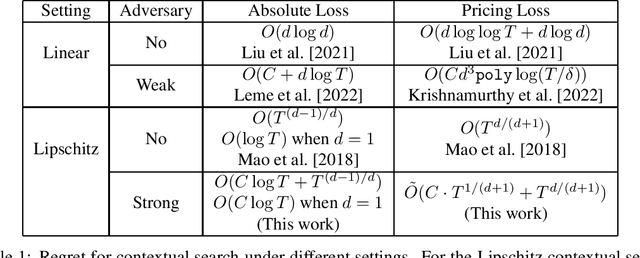
I study the problem of learning a Lipschitz function with corrupted binary signals. The learner tries to learn a Lipschitz function $f$ that the adversary chooses. In each round, the adversary selects a context vector $x_t$ in the input space, and the learner makes a guess to the true function value $f(x_t)$ and receives a binary signal indicating whether the guess was high or low. In a total of $C$ rounds, the signal may be corrupted, though the value of $C$ is unknown to the learner. The learner's goal is to incur a small cumulative loss. I present a natural yet powerful technique sanity check, which proves useful in designing corruption-robust algorithms. I design algorithms which (treating the Lipschitz parameter $L$ as constant): for the symmetric loss, the learner achieves regret $O(C\log T)$ with $d = 1$ and $O_d(C\log T + T^{(d-1)/d})$ with $d > 1$; for the pricing loss the learner achieves regret $\widetilde{O} (T^{d/(d+1)} + C\cdot T^{1/(d+1)})$.

TRS: Transferability Reduced Ensemble via Encouraging Gradient Diversity and Model Smoothness

Adversarial Transferability is an intriguing property of adversarial examples -- a perturbation that is crafted against one model is also effective against another model, which may arise from a different model family or training process. To better protect ML systems against adversarial attacks, several questions are raised: what are the sufficient conditions for adversarial transferability? Is it possible to bound such transferability? Is there a way to reduce the transferability in order to improve the robustness of an ensemble ML model? To answer these questions, we first theoretically analyze sufficient conditions for transferability between models and propose a practical algorithm to reduce transferability within an ensemble to improve its robustness. Our theoretical analysis shows only the orthogonality between gradients of different models is not enough to ensure low adversarial transferability: the model smoothness is also an important factor. In particular, we provide a lower/upper bound of adversarial transferability based on model gradient similarity for low risk classifiers based on gradient orthogonality and model smoothness. We demonstrate that under the condition of gradient orthogonality, smoother classifiers will guarantee lower adversarial transferability. Furthermore, we propose an effective Transferability Reduced Smooth-ensemble(TRS) training strategy to train a robust ensemble with low transferability by enforcing model smoothness and gradient orthogonality between base models. We conduct extensive experiments on TRS by comparing with other state-of-the-art baselines on different datasets, showing that the proposed TRS outperforms all baselines significantly. We believe our analysis on adversarial transferability will inspire future research towards developing robust ML models taking these adversarial transferability properties into account.

Near Optimal Adversarial Attack on UCB Bandits

We consider a stochastic multi-arm bandit problem where rewards are subject to adversarial corruption. We propose a novel attack strategy that manipulates a UCB principle into pulling some non-optimal target arm $T - o(T)$ times with a cumulative cost that scales as $\sqrt{\log T}$, where $T$ is the number of rounds. We also prove the first lower bound on the cumulative attack cost. Our lower bound matches our upper bound up to $\log \log T$ factors, showing our attack to be near optimal.

A Realistic Example in 2 Dimension that Gradient Descent Takes Exponential Time to Escape Saddle Points

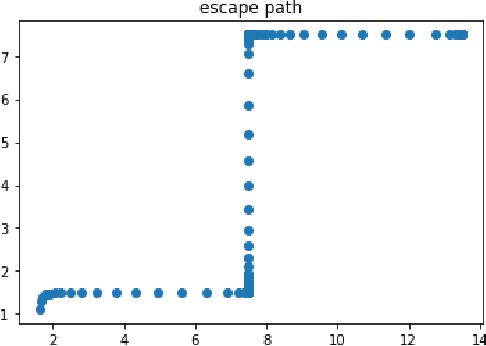
Gradient descent is a popular algorithm in optimization, and its performance in convex settings is mostly well understood. In non-convex settings, it has been shown that gradient descent is able to escape saddle points asymptotically and converge to local minimizers [Lee et. al. 2016]. Recent studies also show a perturbed version of gradient descent is enough to escape saddle points efficiently [Jin et. al. 2015, Ge et. al. 2017]. In this paper we show a negative result: gradient descent may take exponential time to escape saddle points, with non-pathological two dimensional functions. While our focus is theoretical, we also conduct experiments verifying our theoretical result. Through our analysis we demonstrate that stochasticity is essential to escape saddle points efficiently.