IMBERT: Making BERT Immune to Insertion-based Backdoor Attacks

Backdoor attacks are an insidious security threat against machine learning models. Adversaries can manipulate the predictions of compromised models by inserting triggers into the training phase. Various backdoor attacks have been devised which can achieve nearly perfect attack success without affecting model predictions for clean inputs. Means of mitigating such vulnerabilities are underdeveloped, especially in natural language processing. To fill this gap, we introduce IMBERT, which uses either gradients or self-attention scores derived from victim models to self-defend against backdoor attacks at inference time. Our empirical studies demonstrate that IMBERT can effectively identify up to 98.5% of inserted triggers. Thus, it significantly reduces the attack success rate while attaining competitive accuracy on the clean dataset across widespread insertion-based attacks compared to two baselines. Finally, we show that our approach is model-agnostic, and can be easily ported to several pre-trained transformer models.

Mitigating Backdoor Poisoning Attacks through the Lens of Spurious Correlation

Modern NLP models are often trained over large untrusted datasets, raising the potential for a malicious adversary to compromise model behaviour. For instance, backdoors can be implanted through crafting training instances with a specific textual trigger and a target label. This paper posits that backdoor poisoning attacks exhibit spurious correlation between simple text features and classification labels, and accordingly, proposes methods for mitigating spurious correlation as means of defence. Our empirical study reveals that the malicious triggers are highly correlated to their target labels; therefore such correlations are extremely distinguishable compared to those scores of benign features, and can be used to filter out potentially problematic instances. Compared with several existing defences, our defence method significantly reduces attack success rates across backdoor attacks, and in the case of insertion based attacks, our method provides a near-perfect defence.

TRS: Transferability Reduced Ensemble via Encouraging Gradient Diversity and Model Smoothness

Adversarial Transferability is an intriguing property of adversarial examples -- a perturbation that is crafted against one model is also effective against another model, which may arise from a different model family or training process. To better protect ML systems against adversarial attacks, several questions are raised: what are the sufficient conditions for adversarial transferability? Is it possible to bound such transferability? Is there a way to reduce the transferability in order to improve the robustness of an ensemble ML model? To answer these questions, we first theoretically analyze sufficient conditions for transferability between models and propose a practical algorithm to reduce transferability within an ensemble to improve its robustness. Our theoretical analysis shows only the orthogonality between gradients of different models is not enough to ensure low adversarial transferability: the model smoothness is also an important factor. In particular, we provide a lower/upper bound of adversarial transferability based on model gradient similarity for low risk classifiers based on gradient orthogonality and model smoothness. We demonstrate that under the condition of gradient orthogonality, smoother classifiers will guarantee lower adversarial transferability. Furthermore, we propose an effective Transferability Reduced Smooth-ensemble(TRS) training strategy to train a robust ensemble with low transferability by enforcing model smoothness and gradient orthogonality between base models. We conduct extensive experiments on TRS by comparing with other state-of-the-art baselines on different datasets, showing that the proposed TRS outperforms all baselines significantly. We believe our analysis on adversarial transferability will inspire future research towards developing robust ML models taking these adversarial transferability properties into account.

Bayesian Differential Privacy through Posterior Sampling

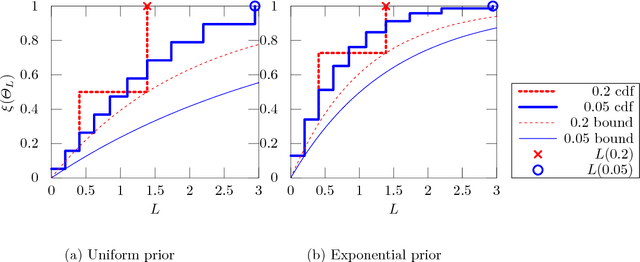
Differential privacy formalises privacy-preserving mechanisms that provide access to a database. We pose the question of whether Bayesian inference itself can be used directly to provide private access to data, with no modification. The answer is affirmative: under certain conditions on the prior, sampling from the posterior distribution can be used to achieve a desired level of privacy and utility. To do so, we generalise differential privacy to arbitrary dataset metrics, outcome spaces and distribution families. This allows us to also deal with non-i.i.d or non-tabular datasets. We prove bounds on the sensitivity of the posterior to the data, which gives a measure of robustness. We also show how to use posterior sampling to provide differentially private responses to queries, within a decision-theoretic framework. Finally, we provide bounds on the utility and on the distinguishability of datasets. The latter are complemented by a novel use of Le Cam's method to obtain lower bounds. All our general results hold for arbitrary database metrics, including those for the common definition of differential privacy. For specific choices of the metric, we give a number of examples satisfying our assumptions.

On the Differential Privacy of Bayesian Inference

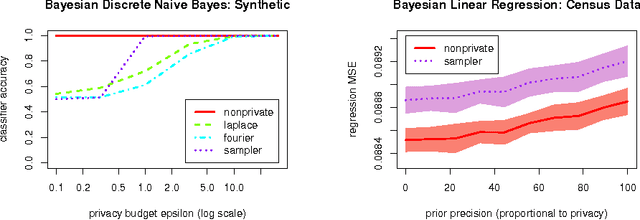
We study how to communicate findings of Bayesian inference to third parties, while preserving the strong guarantee of differential privacy. Our main contributions are four different algorithms for private Bayesian inference on proba-bilistic graphical models. These include two mechanisms for adding noise to the Bayesian updates, either directly to the posterior parameters, or to their Fourier transform so as to preserve update consistency. We also utilise a recently introduced posterior sampling mechanism, for which we prove bounds for the specific but general case of discrete Bayesian networks; and we introduce a maximum-a-posteriori private mechanism. Our analysis includes utility and privacy bounds, with a novel focus on the influence of graph structure on privacy. Worked examples and experiments with Bayesian na{\"i}ve Bayes and Bayesian linear regression illustrate the application of our mechanisms.