On the Differential Privacy of Bayesian Inference
Paper and Code
Dec 22, 2015
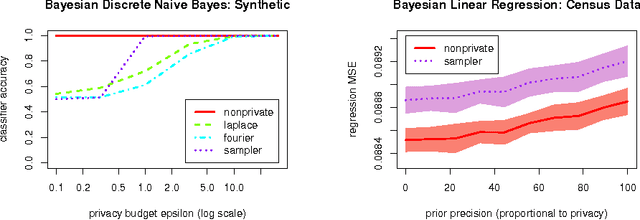
We study how to communicate findings of Bayesian inference to third parties, while preserving the strong guarantee of differential privacy. Our main contributions are four different algorithms for private Bayesian inference on proba-bilistic graphical models. These include two mechanisms for adding noise to the Bayesian updates, either directly to the posterior parameters, or to their Fourier transform so as to preserve update consistency. We also utilise a recently introduced posterior sampling mechanism, for which we prove bounds for the specific but general case of discrete Bayesian networks; and we introduce a maximum-a-posteriori private mechanism. Our analysis includes utility and privacy bounds, with a novel focus on the influence of graph structure on privacy. Worked examples and experiments with Bayesian na{\"i}ve Bayes and Bayesian linear regression illustrate the application of our mechanisms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge